* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Project 1: Marketing
Survey
Document related concepts
Transcript
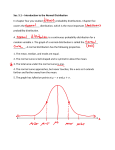
Project 1: Marketing An Introduction Goal Your goal is three-fold: To find the price of a particular product that will maximize profits. Determine the number of units that will be sold at the optimal price. Determine the maximum profit that is expected from the sales of your particular product. Definitions Market: A market is people or organizations with purchasing power and willingness and authority to buy Product: Good or service bought and sold Marketing/Marketing Research Product differentiation is very important in marketing “What makes this any different from product X?” Market can be segmented by age, culture, and interest. http://www.ama.org Marketing Mix -Components 3. Product Planning Distribution Promotion – Advertisements 4. Pricing 1. 2. This is what we are interested in Competition Monopoly: Amount of product depends on price set. There are few perfect (pure) monopolies – usually occur in government regulated services such as gas and electric Sometimes the above examples are called natural monopolies Competition Perfect Competitor: Amount sold does not affect the good’s price Example (from text): Small farmer planting wheat or soybeans. Shifting to either affects neither price at all. Where do we fit? Our company has temporary monopoly power for our product. This means that we have a new product that does not have an exact competitor The functions To achieve the goal of the project, we will need to look at different mathematical functions Recall: What is the definition of a function? We have 4 in particular that we will need to study Demand, Cost, Revenue, and Profit • Note the units on each of the axes for all of the functions Note: We are assuming that we are looking at a monopolistic situation Demand Function, D(q) Gives the unit price, D(q), at which a company can charge in relation to the total quantity (q) of the product that it sells at that price Demand curve, which is the graph of D(q), is generally downward sloping Why? Demand Curve Recall: What does it mean for a curve to be downward sloping? As quantity goes down, what happens to price? As quantity goes up, what happens to price? What should our curve look like? Demand Curve We can look at the curve and see at what unit price we can sell a specified number of items When the unit price is high, the total quantity we sell is low When the unit price is low, the total quantity we sell is high For our purposes we are going to assume that the maximum quantity that can be sold is where the curve intersects the q-axis. Demand Curve, D(q) Unit price, D(q) (in $) Total quantity (q) Perfect Competitor vs. Monopoly For a perfect competitor, if you plot price against quantity sold you get a constant function. Why? What will the two curves look like plotted against each other? Demand Curve, D(q) Monopolist Unit price, D(q) (in $) Perfect Competitor Quantity (q) Revenue Function, R(q) To determine the total revenue you will receive from selling a product, you multiply the total number of goods sold by the unit price of the goods R(q)=D(q)*q Now, if you sell a small amount for a high price, you will have a small revenue If you sell a large amount for a low price, you will have a small revenue What does the curve look like? Revenue Curve We can look at the total revenue that is produced when a specified number of items is sold Our graph, starts out low, gets high, and then goes low again Revenue Curve, R(q) Total Revenue (in $) Quantity (q) Cost Function, C(q) When you are making goods, you will incur costs There are two types: Fixed Costs: Incurred even if units are not produced Variable Costs: Unit-based production • Examples: labor, lighting, etc. What does the curve look like? Cost Curve We can look at the total costs that are incurred when a particular number of goods are produced The more goods that are produced, the higher the total cost Cost Curve, C(q) Total cost (in $) Quantity (q) Profit Function, P(q) When does a company make a profit? Thus, the profit function is total revenue minus total cost or P(q) = R(q) – C(q). When the revenue exceeds the costs When the difference is positive, the company has made a profit When the difference is negative, the company has lost money What does the curve look like? Profit Curve When a small number of units are produced, the total cost will be more than the total revenue As the number of units produced is increased, the total cost starts to reach the total revenue Hence, you will have a negative difference It eventually reaches it (break-even point) and then exceeds it, reaching a maximum point After the maximum point is reached it can only decrease This means that if you start making more and more units, your costs exceed your revenue again – hence a negative difference Profit Curve How does this translate to a graph? Profit Curve, P(q) Total profit (in $) Quantity (q) Class Project: Save-it-All! Save-it-All! developed and patented a new type of computer drive, SXL Features reliability, compact size, and the ability to store 500 MB of information Under the conditions of the patent, Saveit-All! has the exclusive right to produce and market the new technology during the next three years, giving them temporary monopolistic power*. * This will be an assumption for our project Questions to Answer 1. 2. 3. How should they price SXL such that it will produce a maximum profit during the coming year? How many drives can they expect to sell? How much profit might they realize from sales? Research Save-it-All!’s marketing department did research on potential buyers Estimates that there are 120 million potential customers in the national market during the coming year Studied 6 test markets to determine the fraction of the potential buyers who would actually buy SXL at various price levels Assumption: From past experience, they will assume that SXL will have a quadratic demand function Information In Marketing Data.xls, you have the results from the test markets You also know the costs of production Fixed overhead costs of $21,600,000 during coming year Variable costs: • First 500,000 drives -- $115 per drive • Next 600,000 drives -- $100 per drive • Rest of the drives -- $90 per drive Pricing & Production Using the information that is given, Saveit-All! wants to analyze the pricing and production of the product, SXL They want to know a price in order for them to achieve maximum profit They want to know how many they will sell at the optimal price They want to know the maximum profit expected They want to know how sensitive the profit is to changes in optimal quantity They want to know what the consumer surplus will be if the profit is maximized Advertising and Capital Additionally, Save-it-All! wants to know the following: What profit can they expect if the unit price of the drive is $154.49? How much should they pay for advertising if the campaign increases demand for the drives by 10% at all price levels? How would the 10% increase in demand effect the optimal price? Would it be smart if they put $4m into training and streamlining if it reduces the variable production costs by 7% for the coming year? Your project Go on-line and get the team data (in an Excel file) It contains test market data and production cost estimates Also, it has 9 questions that will need to be answered at the end of the project Assume that your company has temporary monopolistic power for the next 3 years Preliminary Report We will follow the course syllabus Everyone will go on the same day – order of presentation will be random Casual dress (no shorts, wrinkled shirts, low cut or short shirts/skirts, flip-flops) Each team will present for about 5-10 minutes Bring a hard copy of your slides for me (handout – 4 slides per page) Be prepared for computer mishaps – have backup or hard copy of slides Preliminary Report Introduce your company and your job descriptions (your choice – be creative) Come up with a unique product that makes sense with the prices given Know basic terms and assumptions Remember product differentiation Do not give list of definitions but work into presentation Present the data Give an initial guess for the max profit How? Initial guess of max profit For each test market, you should calculate the following: Number of units (National Market Size) Market Size This calculation gives you the number of units in the potential national market Multiply that number by the price for that test market This gives you the total revenue for each particular test market Initial guess of max profit Now, you will need to know the total cost for each test market You already know the fixed cost Determine the variable cost for each amount of units (you have 8) by using the variable cost information given Total cost = Fixed Cost + Variable Cost Once you have the total cost for each test market, subtract it from the total revenue from that test market. The greatest number will be your initial guess