Download Stable

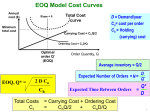
Dr. Ron Lembke
Economic Order Quantity
Assumptions
 Demand rate is known and constant
 No order lead time
 Shortages are not allowed
 Costs:
 S - setup cost per order
 H - holding cost per unit time
EOQ
Inventory
Level
Q*
Optimal
Order
Quantity
Decrease Due to
Constant Demand
Instantaneous
Average
Receipt of Optimal
Inventory Q/2
Order Quantity
Time
Total Costs
 Average Inventory = Q/2
 Annual Holding costs = H * Q/2
 # Orders per year = D / Q
 Annual Ordering Costs = S * D/Q
 Annual Total Costs = Holding + Ordering
Q
D
TC (Q)  H *  S *
2
Q
How Much to Order?
Total Cost
Annual Cost
= Holding + Ordering
Ordering Cost
= S * D/Q
Holding Cost
= H * Q/2
Optimal Q
Order Quantity
Optimal Quantity
Total Costs =
Q
D
H* S*
2
Q
Take derivative
with respect to Q =
H
D
S* 2 0
2
Q
Set equal
to zero
Solve for Q:
H DS
 2
2 Q
2 DS
Q 
H
2
2 DS
Q
H
EOQ
Inventory
Level
Q*
Reorder
Point
(R)
Time
Lead Time
Adding Lead Time
2 DS
Q
H
 Order before inventory depleted
 Use same order size
R  dL
 Where:
 d = demand rate (per day)
 L = lead time (in days)
 both in same time period (wks, months, etc.)
A Question:
2 DS
Q
H
 If the EOQ is based on so many horrible assumptions
that are never really true, why is it the most commonly
used ordering policy?
 Cost curve very flat around optimal Q, so a small
change in Q means small increase in Total Costs
 If overestimate D by 10%, and S by 10%, and H by 20%,
they pretty much cancel each other out
 Have to overestimate all in the wrong direction before Q
affected
Sensitivity
 Suppose we do not order optimal Q*, but order Q instead.
 Percentage profit loss given by:
TC (Q) 1  Q * Q 
 


TC (Q*) 2  Q Q * 
 Should order 100, order 150 (50% over):
0.5*(0.66 + 1.5) =1.08 an 8%cost increase
Quantity Discounts- Price Break
 How does this all change if price changes
depending on order size?
 Holding cost as function of cost:
 H=i*C
 Explicitly consider price:
2 DS
Q
i C
Discount Example
D = 10,000
S = $20
Price
C = 5.00
4.50
3.90
Quantity
Q < 500
500-999
Q >= 1000
Must Include
Cost of Goods:
2 DS
Q
i C
i = 20%
EOQ
633
667
716
Q
D
TC (Q)  iC  S  DC
2
Q
Discount Pricing
Total Cost
Price 1
Price 2
Price 3
X 633
X 667
X 716
500
1,000
Order Size
C=$5
C=$4.5
C=$3.9
Discount Example
Order 667 at a time:
Hold 667/2 * 4.50 * 0.2= $300.15
Order 10,000/667 * 20 =
$299.85
Mat’l 10,000*4.50 =
$45,000.00
45,600.00
Order 1,000 at a time:
Hold 1,000/2 * 3.90 * 0.2= $390.00
Order 10,000/1,000 * 20 = $200.00
Mat’l 10,000*3.90 =
$39,000.00
39,590.00
Discount Model
1. Compute EOQ for next cheapest price
2. Is EOQ feasible? (is EOQ in range?)
If EOQ is too small, use lowest possible Q to get
price.
3. Compute total cost for this quantity
4. Repeat until EOQ is feasible or too big.
5. Select quantity/price with lowest total cost.
Summary
 Economic Order Quantity
 Perfectly balances ordering and holding costs
 Very robust, errors in input quantities have small impact
on correctness of results
 Discount Model
 Start with EOQ calculations, using H= iC
 Compute EOQ for each price,


Determine feasible quantity
Compute Total Costs:
 Holding, Ordering, and Cost of Goods.
Dr. Ron Lembke
Random Demand
 Don’t know how many we will sell
 Sales will differ by period
 Average always remains the same
 Standard deviation remains constant
How would our policies change?
 How would our order quantity change?
 EOQ balances ordering vs holding, and is unchanged
 How would our reorder point change?
 That’s a good question
Constant Demand vs Random
•Steady demand
•Always buy Q
•Reorder at R=dL
•Sell dL during LT
•Inv = Q after arrival
•Random demand
•Always buy Q
•Reorder at R=dL + ?
•Sell ? during LT
•Inv = ? after arrival
Inv
Q
R
L
Q
Q
Q
R
L
Random Demand
 Reorder when on-hand inventory is equal to the
amount you expect to sell during LT, plus an extra
amount of safety stock
 Assume daily demand has a normal distribution
 If we want to satisfy all of the demand 95% of the time,
how many standard deviations above the mean should
the inventory level be?
 Just considers a probability of running out, not the
number of units we’ll be short.
Demand over the Lead Time
R = Expected Demand over LT + Safety Stock
R  d L  z L
d = Average demand per day
L = Lead Time in days
 L = st deviation of demand over Lead Time
z from normal table, e.g. z.95 = 1.65
Random Example
 What should our reorder point be?
 Demand averages 50 units per day, L = 5 days
 Total demand over LT has standard deviation of 100
 want to satisfy all demand 90% of the time
 To satisfy 90% of the demand, z = 1.28
R  d L  z L
R  50 * 5  1.28 *100
R  250  128  378
Random Demand
•Random demand
•Always buy Q
•Reorder at R=dL + SS
Inv
R
•Sometimes use SS
•Sometimes don’t
•On average use 0 SS
St Dev of Daily Demand
 What if we only know the average daily demand, and
the standard deviation of daily demand?
 Lead time = 4 days,
 daily demand = 10,
 Daily demand has standard deviation = 5,
 What should our reorder point be, if z = 3?
St Dev Over LT
 If the average each day is 10, and the lead time is 4
days, then the average demand over the lead time must
be 40.
d * L  10 * 4  40
 What is the standard deviation of demand over the
lead time?
 Std. Dev. ≠ 5 * 4
St Dev Over Lead Time
 We can add up variances, not standard deviations
 Standard deviation of demand over LT =
 L  Ldays  day
 45  10
R  d * L  z L  d * L  z Ldays  day
Demand Per Day
R  d L  z * L * D
Or, same
thing:
 L  L * D
R  d L  z L
L = Lead time in days
d = average demand per day
 D = st deviation of demand per day
z from normal table, e.g. z.95 = 1.65
Random Demand
Fixed Order Quantity
 Demand per day averages 40 with standard deviation
15, lead time is 5 days, service level of 90%
L = 5 days
d = 40
 D = 15
z = 1.30,
R  d L  z * L * D
R  40 * 5  1.30 * 5 *15
R  200  43.6  243.6
Fixed-Time Period Model
 Place an order every, say, week.
 Time period is fixed, order quantity will vary
 Order enough so amount on hand plus on order gets
up to a target amount
 Q = S – Inv
 Order “up to” policies
S  d L  T   z * L  T *  D
Service Level Criteria
 Type I: specify probability that you do not run out
during the lead time
 Chance that 100% of customers go home happy
 Type II: (Fill Rate) proportion of demands met from
stock
 100% chance that this many go home happy, on average
Two Types of Service
CycleDemand
1
180
2
75
3
235
4
140
5
180
6
200
7
150
8
90
9
160
10
40
Sum
1,450
Stock-Outs
0
0
45
0
0
10
0
0
0
0
55
Type I:
8 of 10 periods
80% service
Type II:
1,395 / 1,450 =
96%
Summary
 Fixed Order Quantity – always order same
 Random demand – reorder point needs to change
 Standard Deviation over the LT is given
 Standard Deviation per day is given
 Fixed Time Period
 Always order once a month, e.g.
 Amount on hand plus on order will add up to S
 Different service metrics