Download An Introduction to Genetic Algorithms and the application

Institute of Information Science, Academia Sinica
Research Assistant: Lin, Hsin-Nan 林信男
1/67
Outline
 Optimization Problems
 Optimization Techniques
 Genetic Algorithms
 Two brief examples
 NMR Backbone Assignment
2/63
Optimization Problems
 Definition: A computational problem in which the
object is to find the best of all possible solutions.
 Classical optimization problems
 Traveling Salesman Problem
 Knapsack Problem
 Prisoner’s Dilemma
3/63
Search spaces and Fitness Landscapes
 Search Space: Some collection of candidate solutions
to a problem
 Fitness Landscape: A representation of the space of all
possible genotypes along with their fitness.
4/63
Example: Traveling Salesman Problem
5/63
Example: Traveling Salesman Problem
 Search space: n!
 No method can give the optimal solution except
exhaustive searching for all possible solutions.
6/63
Optimization Techniques
 Heuristic methods
 Hill Climbing
 Simulated Annealing
 Genetic Algorithms
 Ant Colony optimization
 …..
7/63
Hill Climbing
 Iterative Improvement
 Start at a random configuration; repeatedly consider
various moves; accept some & reject some. When you’re
stuck, restart
 We must invent a moveset that describes what moves
we will consider from any candidate solution
8/63
Genetic Algorithms
 Search technique based on the principle of evolution
 Survival of the fittest in Natural Selection
 Developed by John Holland, University of Michigan
(1970’s)
 GAs use two basic processes from evolution
 Inheritance (passing of features from one generation to
the next)
 Competition (survival of the fittest)
9/63
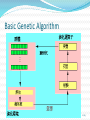
Basic Description of GAs
 Algorithm is started with a set of solutions (represented by
chromosomes) called population.
 Solutions from one population are taken and used to form a
new population.
 The new population (offspring) will be better than the old one
(parent).
 Solutions which are selected to form new solutions are selected
according to their fitness - the more suitable they are the more
chances they have to reproduce.
10/63
Basic Genetic Algorithm
11/63
Operators of GA: Encoding
 The chromosome should in some way contain
information about solution which it represents.
 The most used way of encoding is a binary string.
 Chromosome 1 1101100100110110
 Chromosome 2 1101111000011110
 Each bit in this string can represent some
characteristic of the solution.
 Fixed length or variable length
12/63
Operators of GA: Selection
 Chromosomes are selected from the population to be parents to
crossover.
 According to Darwin's evolution theory the best ones should
survive and create new offspring.
 For example: roulette wheel selection, Boltzman selection,
tournament selection, rank selection, steady state selection and
some others.
13/63
Roulette Wheel Selection
 Parents are selected according to their fitness.
 The better the chromosomes are, the more chances to be
selected they have.
14/63
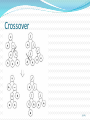
Operators of GA: Crossover
 Crossover selects genes from parent chromosomes and
creates a new offspring.
 Chromosome 111011 | 00100110110
 Chromosome 211000 | 11000011110
 Offspring 1
11011 | 11000011110
 Offspring 2
11000 | 00100110110
 “ | “ is the crossover point
15/63
Crossover
 Single point crossover: 11001011+11011111 = 11001111
 Two point crossover: 11001011 + 11011111 = 11011111
 Uniform crossover: 11001011 + 11011101 = 11011111
 Arithmetic crossover: 11001011 + 11011111 = 11001001
(AND)
16/63
Operators of GA: Mutation
 Prevent falling all solutions in population into a local optimum





of solved problem
Mutation changes randomly the new offspring.
Original offspring 11101111000011110
Mutated offspring 11100111000011110
Original offspring 21101100100110110
Mutated offspring 21101101100110110
17/63
Control Parameters
 Population Size and Generation Number
 GA has two control parameters: crossover rate (pc) and
mutation rate (pm).
 pc (0.5~1.0): The higher the value of pc, the quicker are the
new solutions introduced into the population.
 pm (0.005~0.05): Large values of pm transform the GA into a
purely random search algorithm, while some mutations are
required to prevent the premature convergence of the GA
to suboptimal solutions.
18/63
How Do Genetic Algorithms Work?
 GAs work by discovering, and recombining good
“building blocks” of solutions in a highly parallel
fashion.
 Good solutions tend to be made up of good building
blocks
19/63
An example of building block
 Password Guessing
 Chromosome 1: algehklppr (fitness: 3)
 Chromosome 2: bgrekithms (fitness: 5)
 Child: algehithms (fitness: 8)
20/63
Two Brief Examples
 The strategies for the Prisoner’s Dilemma
 Global Sequence Alignment
21/63
Prisoner’s Dilemma
 Two suspects, A and B, are arrested by the police. The
police have insufficient evidence for a conviction, and,
having separated both prisoners, visit each of them to
offer the same deal:
22/63
The strategies
 If you suspect that your opponent is going to
 cooperate, then you should surely defect.
 defect, then you should defect too.
 The dilemma is
 If both players defect each gets a worse score than if they
cooperate.
 Both players memorize the previous games
 Simple and good strategy: TIC FOR TAT
 Could the GA evolve better strategies ?
23/63
Encoding the Chromosomes
 If memory is one previous game
 CC (case 1)
 CD (case 2)
 DC (case 3)
 DD (case 4)
 Example of TIT FOR TAT
 If CC (case 1), then C
 If CD (case 2), then D
 If DC (case 3), then C
 If DD (case 4), then D
 Encoding the strategies for TIT FOR TAT : CDCD
 Encoding the strategies for “Loyal Guy”: CCCC
24/63
Encoding the Chromosomes
 If memory is the three previous games
 There are 64 possibilities for the previous three games:





CC CC CC (case 1)
CC CC CD (case 2)
…
DD DD DC (case 63)
DD DD DD (case 64)
strategy for case 64
C D C C …. C D D
 Encoding
 a 64-letters string
 CDCCCDDCCCDD…CCCDDD strategy for case 1
 Search space: 264
25/63
Evaluation
 Each individual is playing the game with several fixed
strategies (coach)
 The environment is static.
 For each game, individual could get a payoff according
to the payoff matrix.
Cooperate
Defect
Cooperate
3, 3
0, 5
Defect
5, 0
1, 1
26/63
Observation
 The highest-scoring strategies produced by the GA
were designed to exploit specific weaknesses of the
fixed strategies.
 It is not necessarily true that these high-scoring
strategies would also score well in a different
environment.
 Conclusion: GA is good at doing what evolution often
does: developing highly specialized adaptations to
specific characteristics of the environment.
27/63
Evaluation II
 Take any two individuals (chromosomes) to play the
games iteratively for 100 times.
 Since we randomly generate the populations. The
performance of a strategy depends very much on its
environment (opponents).
 The environment is dynamic.
 The environments are evolving
 The results of evolution are like to the TIC FOR TAT
28/63
Global Sequence Alignment
 In bioinformatics, a sequence alignment is a way of
arranging the primary sequences of DNA, RNA, or
protein to identify regions of similarity that may be a
consequence of functional, structural, or evolutionary
relationships between the sequences.
29/63
Global Sequence Alignment
 A general global alignment technique is called the
Needleman-Wunsch algorithm and is based on
dynamic programming.
 To align two sequences in length m and n


Time Complexity: O(kmn)
Space Complexity: O(kmn)
 If m = 4000, n = 5000

It takes more than 100 MB
30/63
Global Sequence Alignment
 S1 = 【ABC】, S2 = 【BDC】
 The alignments are variable in length
A
B
C
A
B
-
C
-
B
D
C
-
B
D
-
C
A
B
-
C
-
B
D
C
A
B
C
-
-
-
-
-
-
B
D
C
31/63
Global Sequence Alignment using a GA
 Encoding
 Chromosome Length: 2(m+n )(the maximum length of
the alignment)


The first m+n  the alignment result of first sequence
The second m+n  the alignment result of second sequence
 Binary bit string


1: a character in the sequence
0: a gap
32/63
Encoding
 Example:
 S=“AAAC”, T=“AGC”
A
A
A
C
A
-
G
C
 chromosome=11110001011000
1
1
1
1
0
0
0
A
A
A
C
-
-
-
A
-
G
C
-
-
-
1
0
1
1
0
0
0
33/63
Encoding Constraints
 The first half of m+n bit string must contain m 1’s
 Represents the m characters of the first sequence
 The second half of m+n bit sting must contain n 1’s
 Represents the n characters of the second sequence
chromosome=11110001011000
1
1
1
1
0
0
0
A
A
A
C
-
-
-
A
-
G
C
-
-
-
1
0
1
1
0
0
0
34/63
Evalution
 As the same as the dynamic programming method
 +2: if xi = yj
 -2: if xi ≠ yj
 -1: gap penality (if xi aligns a gap or yj aligns a gap )
35/63
Crossover
 Could not simply perform the normal crossover
operation.
 It must satisfy the encoding constraints.
P1
1
1
1
1
0
0
0
1
0
1
1
0
0
0
P2
1
0
1
1
1
0
0
1
0
0
1
1
0
0
child
1
1
1
1
1
0
0
1
0
0
1
1
0
0
child
1
1
1
1
0
0
0
1
0
0
1
1
0
0
36/63
An Extra Example for variable length of the
chromosome encoding
 Genetic programming
 Evolving Lisp Programs
 Example: design a program to compute the orbital
period P of a planet given its average distance A from
the sun.
 Kepler’s Third Law: P2 = cA3
 In FORTRAN: P = SQRT(A*A*A)
 In Lsip: (SQRT(*A(*AA)))
37/63
Encoding
 Choose a set of possible functions and terminals for
the programs.
 Functions: {+, -, *, /, √}
 Terminal: A
38/63
Crossover
39/63
A GP demo on the web
 http://alphard.ethz.ch/gerber/approx/default.html
40/63
A GA demo on the web
 http://www.see.ed.ac.uk/~rjt/ga.html?http://oldeee.se
e.ed.ac.uk/~rjt/ga.html
41/63
Other applications
 Classification
 Scheduling
 TSP
 http://www.ads.tuwien.ac.at/raidl/tspga/TSPGA.html
 Computer-Aided Design
 Composing music with GA.
42/63
43
Data Source: Three important experiments
44/63
HSQC Spectra
 HSQC peaks (1 chemical shifts for an amino acid)
H
N
Intensity
8.109
118.60
65920032
45/63
CBCANH Spectra
 CBCANH peaks (4 chemical shifts for one amino
acid)
 Ca (+), Cb (-)
H
N
C
Intensity
8.116
118.25
16.37
79238811
8.109
118.60
36.52
-65920032
8.117
118.90
61.58
-51223894
8.119
117.25
57.42
109928374
46/63
CBCA(CO)NH Spectra
 CBCA(CO)NH peaks (2 chemical shifts for one
amino acid)
H
N
C
Intensity
8.116
118.25
16.37
79238811
8.109
118.60
36.52
65920032
47/63
Spin System Groups
 A spin system contains the chemical shifts of atoms
within a residue.
 A spin system group contain two spin systems, one is
from inter-residue and the other is from intra-residue.
Inter-residue’s spin system, SSinter
(i)
Intra-residue’s spin system SSintra (i)
48/63
Chemical Shift Ranges of Amino Acids
Some amino acids have
particular chemical shift
ranges, some share common
chemical shift rages.
Chemical shift ranges of Ala, CS(A)
14 < Cb < 24
15 < Ca < 72
49/63
Ambiguities
 All 4 point experiments are mixed together
 All 2 point experiments are mixed together
 Each spin system can be mapped to several amino
acids in the protein sequence
 False positives, false negatives
50/63
Ambiguous Spin System
N
H
Intensity
106.9 8.87 423879
106.9 8.87 524522
N
H
C
106.91 8.85 59.7
Intensity
235673
106.92 8.86 54.93 346234
106.91 8.86 61.5
432432
106.91 8.85 40.31 -335759
106.92 8.86 30.5
-483759
51/63
Candidate Lists
M
L
K
V
A
R
S
T
Candidate list of R, CL(R) =
{ x | SSinter (x) is within CS(A) and
SSintra (x) is within CS(R) }
CL(L) = {1, 4, 17, 28, 33, 40, 52, 65}
CL(K) = {2, 9, 11, 19, 21, 38, 45, 47, 57, 60, 79}
CL(V) = {3, 8, 10, 12, 15, 18, 22, 29, 30, 32, 49, 51}
……
52/63
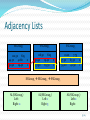
Adjacency Lists
SSGroup1
SSGroup2
SSGroup3
122.30 8.15
44.30
41.80
0
51.90
19.40
1
116.50
8.25
51.90
19.40
0
57.50
63.30
1
111.20
7.75
57.50
63.30
0
34.20
42.90
1
SSGroup1  SSGroup2  SSGroup3
AL(SSGroup1)
Left:
Right: 2
AL(SSGroup2)
Left:1
Right:3
AL(SSGroup3)
Left:2
Right:
53/63
Likes a puzzle game
54/63
Using a Genetic Algorithm
1
5
11
x
18
25
29
43
17
 Step1. Randomly select a position x
 Step2. Randomly select a SSGroup i from CL(x)
 Step3. Extend connected fragments from i to both sides
by using adjacency lists until no more extension can be
found.
 Step4. Repeat Step1~Step3 until all positions are assigned.
55/63
Evaluate the fitness of each
individual
1
5
11
x
18
25
29
43
17
Fitness(ch) = The number of connected pairs associate
with their chemical shift differences.
Two principles:
1. The more connected pairs it has, the higher score it gets.
2. The less chemical shift differences it has, the higher score it gets.
56/63
Crossover operatoin
 Inherit continuous connected fragments from parents.
Parents
Child
57/63
Mutation operations
 Once a position is going to mutate, the following
positions will also mutate to produce a connected
fragments.
Child
Mutant
Mutation point
58/63
Experiment Design: Simulated Error Data
 False Positive
 75% error data
 False Negative
 50% error
 Linking Error
 Ca: +- 0.2
 Cb: +- 0.4
 Combined Error
59/63
Experiment Results
 The accuracy on two real dataset
 SBD:95.1% (FP: 67%)
 LBD:100% (FP: 48%)
 The average accuracy on perfect BMRB datasets (902
proteins)
60/63
Compare with MARS
61/63
Compare with PACES
62/63
Reference
 An Introduction to Genetic Algorithms
 Melanie Mitchell, The MIT Press
 Genetic Algorithm
 Ming-Feng Yeh
 GANA–A Genetic Algorithm for NMR Backbone
Resonance Assignment
 Nucleic Acids Research, 2005, Vol. 33, No. 14
63/63
Programming Projects
 NMR Backbone Assignment
 Consecutive one’s
64/63