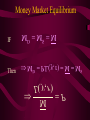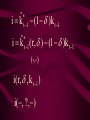Download Topic 5 Money & Investment

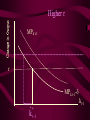
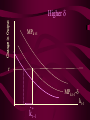
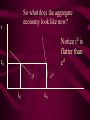
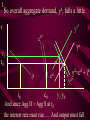
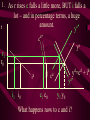
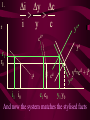
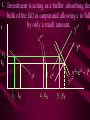
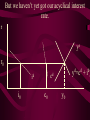
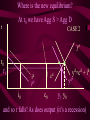
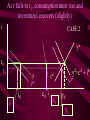
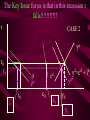
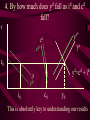
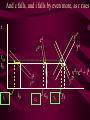
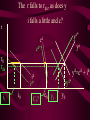
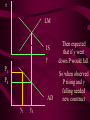
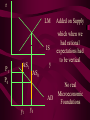
Before we consider investment in the
model however, we should very briefly
look at what is happening to money here
ys
r0
yd
y0
First notice that the
market for goods
determines
real income (y)
and the
real interest rate (r)
•So the money market determines the
nominal variables in the economy:
•The price level
P,
•Inflation
p
•Nominal interest rate
R= r+ p

First consider the Demand for
Money
MD = P L (y, R)
L (+,-)
That is, the demand for money depends
on the level of real income and the
NOMINAL interest rate
Why Nominal?
Because lose R on all money held
First consider the Demand for
Money
P
MD = P L (Y, R)
e.g Suppose we figure out L(y, R)= 8
then
MD = 8P
MD
M
Finding Money Market Equilibrium
For simplicity assume for now that there
is no inflation, p=0
and thus R=r (that is there is no
distinction)
Money Demand must equal Money
supply
 M D  MS  
Money Market Equilibrium
IF
M D  MS  
Then
 M D  P.L( y, r )    MS
L( y , r )

P

Money Market Equilibrium
P
MD
L( y 0 , r0 )
 P0


Money Market Equilibrium
MD
P0
MbD

What happens
now if there is a
Boom?
MD rises as y
rises and r goes
down L(+,-)
So at every P
more is
demanded
Money Market Equilibrium
MD
P0
MbD
P1

So where is the
new
Equilibrium?
So the price
level has fallen
in a boom as
predicted by
the stylised
facts
Money Market Equilibrium
MrD
P1
MD
P0
Similarly in a
recession MD falls
as y falls and r
goes up
Md =PL(y

,r )
And the price
level rises in a
recession
Money Market Equilibrium
Inflation!
P1
MD
P0
0
1
What happens if
the monetary
authority increases
the money supply
It just
causes P to
rise!
Business Cycle Model with Investment
y=f(kt-1,Lt)
y
y=f(kt-1)
y=f(+,+)
Note
production
depends on the
capital stock in
place at the end
of last period
kt-1
y=f(kt-1)
y
Note we are
treating L as a
constant here
y=f(kt-1,Lt)
kt-1
MPk t-1
Marginal
Product of
Capital is
decreasing
kt-1
y
y=f(kt-1)
Note we are
treating L as a
constant here
y=f(kt-1,Lt)
kt-1
y=f(L)
L
But we are
treating kt-1
as a constant
here
y=f(kt-1,Lt)
y
y=f(kt-1)
kt-1
y=f(L)
L
And both
functions
exhibit
diminishing
marginal
returns
More generally could consider
changes in K & L and then would
expect something more like:
2y
y
k&L
2k & 2L
However,
right now we
want to
focus on the
investment
decision so
we need to
focus on
capital in
isolation
y=f(kt-1)
y
MPk t-1
kt-1
And on the
MPkt-1 in
particular
Why?
kt-1
However,
right now we
want to
focus on the
investment
decision so
we need to
focus on
capital in
isolation
y=f(kt-1)
y
kt-1
MPk t-1
kt-1
Because the
MPkt-1 tells
us the
additional
output we
get from one
more unit of
Capital
MPk t-1
What other
consideration do we
need to think about
with capital?
Depreciation!
kt-1
MPk t-1
So true return from
capital is MPkt-1 less
depreciation, d.
What is its cost?
The real rate of
interest r
MPk t-1-d
kt-1
MPk t-1
So we should equate
the real return on
capital, MPkt-1-d,
with the real rate of
interest r
r
MPk t-1-d
kt-1
k̂
*
t 1
k̂
MPk t-1
*
t 1
Is the desired
capital stock
r
MPk t-1-d
kt-1
k̂
*
t 1
MPk t-1
Note a rise in r or
d results in a
lower desired
capital stock
r
MPk t-1-d
kt-1
k̂
*
t 1
Higher r
MPk t-1
r
MPk t-1-d
kt-1
k̂
*
t 1
Higher d
MPk t-1
r
MPk t-1-d
kt-1
k̂
*
t 1
MPk t-1
k̂ (r, d )
*
t 1
k̂ (,)
*
t 1
r
MPk t-1-d
kt-1
k̂
*
t 1
k̂
*
t 1
Desired Capital Stock
But we are interested in investment, not
desired capital stock
How do we get from desired capital
stock to investment?
Investment is the difference between the
desired capital stock, and the existing
capital stock
Investment is the difference between
the desired capital stock, and the
existing capital stock
Existing Capital Stock:
Capital in place last period less
whatever wore out.
(1-d)kt-1
Investment is the difference between
the desired capital stock, and the
existing capital stock
i  k̂
*
t 1
 (1  d )k t 1
i  k̂
*
t 1
 (1  d )k t 1
i  k̂ (r, d )  (1  d )k t 1
*
t 1
(-,-)
i(r, d , k t1 )
i(, ,)
But what about d?
i  k̂
*
t 1
 (1  d )k t 1
i  k̂ (r, d )  (1  d )k t 1
*
t 1
(-,-)
i(r, d , k t1 )
i(, ? ,)
r
i(r, d , k t1 )
id
i
r
Empirically we know that:
di dc

dr dr
And…
id
i
r
c i
: : is approximat ely 4 : 1
y y
Id
I
So what does the aggregate
economy look like now?
r
Notice id is
flatter than
cd
r0
cd
id
i0
c0
And total aggregate
demand is id plus cd
r
r0
cd
id
i0
yd=cd + id)
c0
y0
r
And equilibrium depends on
aggregate demand and supply
ys
r0
cd
id
i0
yd=cd + id)
c0
y0
So now we have described the model with
Investment..
r
ys
r0
id
cd
yd=cd + id)
i0
c0
y0
And we are now in a position to return to our
business cycle shocks.
1. Lets revisit a temporary negative productivity
(Supply) shock and ASSUME that the MPk has
not changed
r
ys*
ys
r0
cd
id
i0
yd=cd + id)
c0
y0
Temporary shock so what happens to cd, id &yd ?
1. Now cd falls a little but the id cirve is not
affected since MPk has not changed
r
ys*
cd*
ys
r0
cd
id
i0
yd=cd + id)
c0
y0
So overall aggregate demand, yd, fall a little
1.
So overall aggregate demand, yd, falls a little
r
ys*
cd*
ys
r1
r0
cd
id
i0
yd=cd + id)
c0
yd*
y1 y0
And since Agg D > Agg S at r0
the interest rate must rise…. And output must fall
1. As r rises c falls a little more, BUT i falls a
lot – and in percentage terms, a huge
amount.
ys*
r
cd*
ys
r1
r0
cd
id
i1 i0
yd=cd + id)
c1 c0
yd*
y1 y0
What happens now to c and i?
1.
r
i y c


i
y
c
ys*
cd*
ys
r1
r0
id
cd
yd=cd + id)
yd*
i1 i0
c1 c0
y1 y0
And now the system matches the stylised facts
1. Investment is acting as a buffer, absorbing the
bulk of the fall in output and allowing c to fall
by only a small amount. ys*
r
cd*
ys
r1
r0
cd
id
i1 i0
yd=cd + id)
c1 c0
yd*
y1 y0
But we haven’t yet got our acyclical interest
rate.
r
ys
r0
cd
id
i0
yd=cd + id)
c0
y0
ASSUME now that a temporary negative shock
reduces the MPk in the future ONLY.
r
CASE 2
ys
r0
cd
id
i0
yd=cd + id)
c0
y0
Output today is unaffected. No change in ys
ASSUME now that a temporary negative shock
reduces the MPk in the future ONLY.
r
CASE 2
ys
r0
cd
id
id*
i0
yd=cd + id)
c0
y0
But if MPk in the future is down, id shifts down today
ASSUME now that a temporary negative shock
reduces the MPk in the future ONLY.
r
CASE 2
ys
r0
cd
id
id*
i0
yd=cd + id)
c0
yd*
y0
…and so the yd curve must shift down also
Where is the new equilibrium?
At r0 we have Agg S > Agg D
r
CASE 2
ys
r0
r1
cd
id
id*
i0
yd=cd + id)
c0
yd*
y1 y0
and so r falls! As does output (it’s a recession)
As r falls to r1, consumption must rise and
investment recovers (slightly)
r
CASE 2
ys
r0
r1
cd
id
id*
i1
i0
yd=cd + id)
c0
c1
yd*
y0
y1
The Key Issue for us is that in this recession r
falls!!!!!!!!!!!
r
CASE 2
ys
r0
r1
cd
id
id*
i1
i0
yd=cd + id)
c0
c1
yd*
y0
y1
Note this is a KEYNESIAN
recession
• We have a fall in the expected
value of future capital returns Mpke
• This is Keynes’ Animal Spirits
• And it manifests itself primarily as
a demand shift
In general would expect a recession to have
elements of both cases 1 & 2
r
ys
r0
id
cd
yd=cd + id)
i0
c0
y0
– shock affect both ys today and future
productivity
So now do both cases together!
r
ys*
ys
cd
r0
yd=cd + id)
id
id*
i0
1.
c0
ys shifts in, as does id
y0
2.
The temporary recession also means
that cd shifts in a little
r
ys*
ys
cd
cd*
r0
yd=cd + id)
id
id*
i0
c0
y0
3. So yd falls also. But now the big Q- By how much?
4. By how much does yd fall as id and cd
fall?
r
ys*
ys
cd
cd*
r0
yd=cd + id)
id
id*
i0
c0
y0
This is absolutely key to understanding our results
4. By how much does yd fall?
r
ys*
ys
cd
cd*
r0
yd=cd + id)
id
yd*
id*
i0
c0
y0
If the shift in yd (&id) is smaller than the shift in ys ..
4. By how much does yd fall?
r
ys*
ys
cd
cd*
rup
r0
yd=cd + id)
id
yd*
id*
i0
c0
y0
Then r rises to rup, and y is down to y1
And c falls, and i falls by even more, as r rises
r
ys*
ys
cd
cd*
rup
r0
yd=cd + id)
id
yd*
id*
i1
i0
c1
c0
y1
y0
4.b But if the shift down in yd is bigger
than the shift in ys
r
ys*
ys
cd
cd*
r0
yd=cd + id)
id
yd*
id*
i0
c0
y0
4.b But if the shift down in yd is bigger
than the shift in ys
r
ys*
ys
cd
cd*
r0
rdn
yd=cd + id)
id
yd*
id*
i0
c0
y0
And r falls to rdn
The r falls to rdn, as does y
i falls a little and c?
r
ys*
ys
cd
cd*
r0
rdn
yd=cd + id)
id
yd*
id*
i1
i0
C1?
c0 y1
y0
TIME FOR A BIG SUMMARY
1.
2.
3.
4.
5.
Negative productivity Shock
Causes ys and id to shift in
cd shifts in a little due to PIH
yd shifts in as cd and id shift in
HOW MUCH DOES yd SHIFT IN
TIME FOR A BIG SUMMARY
5. HOW MUCH DOES yd SHIFT IN
6. If the shift is small
(MPk effect is small)
7. AD > AS
8. r rises, y falls
9. c falls a little
10. i falls a lot
TIME FOR A BIG SUMMARY
5. HOW MUCH DOES yd SHIFT IN
6. If the shift is BIG
(MPk effect is big)
7. AS > AD
8. r falls , y falls
9. c may fall (could even rise-intuition?)
10. i falls
In repeated shocks what would
we see?
1. y falls
2. Sometimes r up, sometimes down
(acyclical)
3. c would fall a little
4. i would fall al lot
5. y down, and change in r = 0 on average
L(y,R) = L(-,0), Md down, so P up
6. Hours worked fall if MPL effect strongest
- from earlier in module
So Now We Have a
Theoretical Model Capable
of Explaining All the
Stylised Facts
So Now We Have a Theoretical
Model Capable of Explaining All the
Stylised Facts
In fairness, some results depend on some
effects being greater or less than others
(e.g. hours worked, interest rates etc)
It is an empirical question whether this is
actually the case.
So Now We Have a Theoretical
Model Capable of Explaining All the
Stylised Facts
So we need to build a model economy like
Chapters, 2, 4, 5 and 12,
with realistic parameters for the
production function, tastes for work and
leisure, and investment function etc
and check whether such an economy can
replicate the observed stylised facts.
Non-Assessed Test Results
40.0
30.0
20.0
10.0
0.0
30<
30-39
40-49
50-59
60-69
More
Most common mistake: Not answering all questions
Evaluation and Assessment
• Readings (on reading list):
• Ryan & Mullineux- The Ups and Downs of
Modern Business Cycle Theory in
Reflections on the Development of Modern
Macroeconomics, Snowden & Vane eds
For a contrary view see paper by Dixon in
same volume
Evaluation and Assessment
• Additional readings which I have placed on the
J drive:
• Ryan - Business Cycle Theory: The Real
Business Cycle in Encyclopaedia of
Macroeconomics (Forthcoming 2002)
• Ryan – Business Cycle Theory: The Stylised
Facts Real Business Cycle in Encyclopaedia of
Macroeconomics (Forthcoming 2002)
What follows is no
substitute for reading Ryan
& Mullineux
Origins of the Real Business
Cycle Theory
1. Theoretical Failures & Add ons
2. Lucas Critique
Origins of the Real Business
Cycle Theory
1. Theoretical Failures & Add ons
r
LM
IS
y
1970’s No
Supply side
in ISLM
Model
Demand
Side model
Only
r
LM
IS
y
P1
P0
AD
y1
y0
Then expected
that if y went
down P would fall.
So when observed
P rising and y
falling needed
new construct
r
P1
P0
LM
Added on Supply
IS
which when we
had rational
expectations had
to be vertical
y
AS1
AS0
AD
y1
y0
No real
Microeconomic
Foundations
Origins of the Real Business
Cycle
2. Lucas Critique
Can’t use reduced forms to evaluate policy
e.g. recall macro last year y=c+i+G-T
If c=a+byd where yd is disposable income
and yd=(1-t)y
Then dy
1
dG

1  b(1  t )
40.0
30.0
20.0
10.0
0.0
30<
30-39
40-49
50-59
60-69
More