* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Survey
Document related concepts
Transcript
Final Notes on Growth and Saving
1
Agenda for this week
•
•
•
•
•
•
Paper assignment
Simulation of increased saving experiment
Advanced macro on “optimal economic growth”
An example from economics of global warming
Alternative schools: Real Business Cycles
Debt, deficits, and growth
2
Paper Assignment
The paper should be 3 to 5 pages (double-spaced, printed, plus tables, figures, and references).
It will count as 10 percent of the course grade.
The paper must left in the box outside Ms. King’s office at 28 Hillhouse Avenue before noon on
Thursday, December 10.
Guidelines are that the paper must: (a) be a topic in macroeconomics, (b) consider economic
history or policy, (c) present evidence and data, and (d) be an application of
macroeconomic analysis.
Some examples of topics would be the following:
- Administration X’s theories and policies, and their successes and/or failures
- The demise of the gold standard or Bretton Woods
- The role of the housing price decline in the current recession
- The legacy of Alan Greenspan, Paul Volcker, or Ronald Reagan
- The macroeconomic effects of protectionism in the Great Depression.
You should consult with your Teaching Fellow about your topic to make sure that it makes
sense and to get ideas for sources.
Consult rules on intellectual honesty and attribution, and don’t procrastinate.
See notes on web site for further information.
3
3
Numerical Example of Budget Surplus in
Neoclassical Growth Model
Assumptions:
1. Production is by Cobb-Douglas with CRTS
2. Labor plus labor-augmenting TC:
1.
n = 1.5 % p.a.; h = 1.5 % p.a.
3. Full employment; constant labor force participation rate.
4. Savings assumption:
a. Private savings rate = 18 % of GDP
b. Initial govt. savings rate = minus 2 % of GDP
c. In 1992, govt. changes fiscal policy and runs a surplus of 2 %
of GDP
d. All of higher govt. S goes into national S (i.e., constant
private savings rate)
5.
“Calibrate” to U.S. economy of 1997
4
Impact of Increased Government Saving on Major Variables
1990
1995
2000
2005
2010
35%
Percent change from baseline
30%
25%
20%
15%
Consumption per capita
GDP per capita
Capital per capita
NNP per capita
- Note that takes 10
years to increase C
-Political
implications
- Must C increase?
10%
5%
0%
-5%
5
-10%
Results on Growth Rates:
Growth rates of Potential
1982-1992
1992-2002
2002-2012
2012-2052
2052-2092
-
NNP
NNP per
capita
GDP per
capita
Consumption
per capita
3.02%
3.28%
3.11%
3.03%
3.02%
1.50%
1.75%
1.59%
1.51%
1.50%
1.50%
1.97%
1.69%
1.53%
1.50%
1.50%
1.47%
1.69%
1.53%
1.50%
Modest impact on growth in short run
Consumption down then up
No impact on growth in long run
GDP v NNP (gross v. net; national v. domestic)
6
Return to question of whether can have too
high a savings rate
- Recall question from last time of whether C has to
increase when S increases.
- This involves the question of whether K is above the
“Golden Rule” K.
- Golden Rule = maximum sustainable level of per capita
consumption
- Simple algebra (consider only net output):
Max f(k) – nk → f’(k) – n = 0 → r = n
or real interest rate = growth rate
7
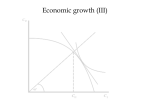
1. Find k** where net interest rate equals n.
2. At that point c is maximized.
This is the golden rule savings rate.
y = f(k)
y
Yale?
c** = (1-s**)f(k**)
(n+δ)k
i = sf(k)
k**
k
8
More general approach: Ramsey-Koopmans model
The Ramsey problem is to determine the optimal savings rate.
Here, we treat that with labor-augmenting technological change
and a specific utility function.
max
{ ct }
t 0
LtU (c t )e t dt
c t C t / Lt (1 st ) F(K t , Et Lt )
dK t / dt st F(K t , Et Lt ) K t
U (c t ) [(c t1 1) /(1 )
We can use different techniques. One is the "calculus of variations,"
which leads to the following "Euler equation":
rt MPK t gt n , where gt rate of growth of per capita consumption
In steady state, t his is:
r * MPK * h n
9
Ramsey-Koopmans model (cont.)
In the polar case of =h=0, this yields the Golden Rule.
However, in cases with or h or >0, get higher r and lower net s.
Conventional discounting:
ρ = 2 % per year; h=2 %; n = 1 %; = 2 r = 5%; s** = 14%
Stern (British economist) argues for low discounting:
ρ = 0.1 %; h=1.3 %; n = 0 %; = 1 r = 1.4 %; s** = 31%
Current US savings rate about 5 - 10 %!
Policy importance:
Say you are worried about the damages from global warming in 2000 yrs.
Say damages are 50 % of output of $50 trillion plus growth
- With conventional discounting, .5*50*exp(200*.02)exp(-.05*200) = $.061
- With Stern discounting, .5*50*exp(200*.013)exp(-.014*200) = $20.5
10
Example of modeling: Yale RICE model
Regional Integrated model of Climate and the Economy
Integrates economic growth, CO2 emissions, climate
change, damages, and economic policy
Relies upon:
- Solow growth model
- Ramsey-Koopmans optimal growth theory
- Samuelson theory of public goods
- wide variety of geophysical theories
- Pigovian theory of externality taxes
11
Results of Solow-Ramsey-Koopmans model
60
GDP (trillions, 2005 US$)
50
40
US
EU
Japan
Russia
China
India
Latin America
30
20
10
0
2005 2015 2025 2035 2045 2055 2065 2075 2085 2095 2105
12
Integration with Climate model and alternative policies
6.0
Temperature
Optimal
Global mean temperature (degrees C)
Baseline
5.0
Lim T<2
Copenhagen trade
4.0
3.0
2.0
1.0
0.0
2005
2025
2045
2065
2085
2105
2125
2145
2165
2185
2205
13
Growth Accounting (not covered in class)
Growth accounting is a widely used technique used to separate out the sources
of growth in a country relies on the neoclassical growth model
Derivation
Start with production function and competitive assumptions. For
simplicity, assume a Cobb-Douglas production function with laboraugmenting technological change:
(1) Yt = At Kt α Lt 1-α
Take logarithms and time derivatives:
(2) ∂ln(Yt)/∂t= gY = gA + α gK + (1 - α) gL
In the C-D, α is the competitive share of K = sh(K); (1 - α) = sh(L).
(3) gY = gA + sh(K) gK + sh(L) gL
From this, we estimate the rate of TC as:
(4) TFP growth = T.C. = gA = gY - sh(K) gK - sh(L) gL
Note that this is a very practical formula. All terms except h are observable.
Can be used to understand the sources of growth in different times and
places.
14
Some applications (not to be covered)
1. Clinton’s growth policy (see above)
2. U.S. growth since 1948
3. China in central planning and reform period
4. Soviet Union growth, 1929 - 1965
The very rapid (measured) growth in the Soviet economy
came primarily from growth in inputs, not from TFP growth.
5. Japanese growth, 1950-75
Japan had very large TFP growth after WWII. Wide variety
of sources, including adoption of foreign
[These are contained in the slides for growth theory.]
15
Classical themes in macroeconomics:
Real Business Cycle Theory
16
Schools of Macroeconomics
longrun
Classical
or non-classical?
(sticky wages
and prices, rational
expectations, etc.
Short run or long run?
(full adjustment of
capital,
expectations, etc.
shortrun
yes
no
yes
Classical
or non-classical?
(sticky wages
and prices, rational
expectations, etc.
no
Neo-classical
growth
model
Marxist theories?
Behavior growth theories?
Malthusian trap models?
Real business cycle (RBC);
supply-side economics;
structural models;
misperceptions models
Keynesian model
(sloping AS,
expectationsaugmented
PC, IS-LM, etc.)
Real Business Cycles
Basic idea: cycles are caused by productivity shocks; these are
propagated by changes in prices and then to labor supply.
Model Details
• Start with neoclassical growth model.
• Remember decomposition of output growth from growth accounting:
gY = α gK + (1-α) gL + θ, where θ = T.C.
• Changes in output come from two sources:
– Technological shocks: θ random.
– Changes in labor force participation: assumes very high
elasticity of labor supply with respect to wages.
• This then generates random output fluctuations, which RBC school
calls business cycles.
RBC recession
Price (P)
AS’
AS
P*
AD
Q*
Real output (Q)
1.12
1.10
Price of GDP
1.08
AS2004:Q4
1.06
1.04
AS2001:Q1
1.02
1.00
9,800 10,000 10,200 10,400 10,600 10,800 11,000
Real GDP
Policy implications of RBC models
• Output shocks are exogenous phenomena (earthquakes, Internet
revolution, terrorist strikes, wars, etc.).
• No role for monetary or fiscal policies in cycle:
– Economy and unemployment are efficient; no need for policies
– Cycles are supply-driven, cannot use AD policies to stabilize output.
– Money is “neutral” (M policy cannot affect real output), so cannot use
M policy
Problems in RBC models
1. Cyclical properties of classical models of the business cycle
- Hard to explain deep recessions and depressions (1930s, 200709) as technological regress.
2. Money and output: is money neutral?
- RBC predicts money neutral
- F/S and Keynesians: much evidence that M is non-neutral
3. Labor market features (such as quits and Beveridge curve)
Verdict: Economists deeply divided.
Personal view: Keynesian approach has not developed a complete
microeconomic justification, but it is most promising approach to
understanding sources and policies for business cycles.
Growth and savings in an open economy?
• For small open economy
– What happens if savings rate increases?
– In this case the marginal investment is abroad!
23
Open economy growth with mobile financial capital ( r = world r = rw)
NX = S - I
S0
r = real
interest rate
r = rw
Original
NX
deficit
I(r)
0
I, S, NX
24
Open economy growth
S1
S0
r = real
interest rate
Higher saving:
1. No change I
2. No change GDP
3. Higher foreign saving
4. Increase GNP, NNP
Final NX
surplus
r = rw
Original
NX
deficit
I(r)
0
I, S, NX
25
y = f(kd)+rkf
yd = f(kd)
(n+δ)k
sy
kd
k
k
26
What if savings in an open economy?
• For small open economy
– What happens if savings rate increases?
– In this case the marginal investment is abroad!
– Therefore, same result, but impact is upon net foreign
assets, investment earnings, and not on domestic capital
stock and domestic income.
– No diminishing returns to investment (fixed r=rw)
– Will show up in NNP not in GDP!
(Most macro models get this wrong.)
• Large open economy like US:
– Somewhere in between small open and closed.
– I.e., some increase in domestic I and some in increase net
foreign assets
27
1. Do Deficits Matter? The Ricardian Theory of the Debt
1. Robert Barro (Chicago/Harvard) introduced a theory in which
deficits do not affect national saving or output.
2. Chicago view of households: They are "clans" or "dynasties" in
which parents have children’s welfare in utility function:
Ui = ui (ci, Ui+1)
where Ui is utility of generation i and
ci is consumption of generation i
3. This implies by substitution:
Ui = ui (ci, ui+1(ci+1, Ui+2)) = vi(ci, ci+1, ci+2, ...)
which is just like an infinitely lived person!
4. Important result: Barro consumers are like a life-cycle model with
infinitely lived agents with perfect foresight:
there will be no impact of anticipated taxes (or deficits) on consumption or on
aggregate demand.
5. Controversial, but empirically questionable. Reasons are myopia,
singles, liquidity constraints, non-altruistic parents.
28