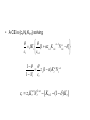Download Real Business Cycles - Villanova University

Real Business Cycles
Motivation
The Model
Solving the Model
Predictions
Fiscal Policy
Readings
• "Understanding Real Business Cycles" by C.
Plosser, Journal of Economic Perspectives 3,
No. 3: 51-77 (Summer 1989)
• “Real Business Cycles: A New Keynesian
Perspective” by N. Gregory Mankiw, Journal of
Economic Perspectives, Vol 3, No 3, pp 79-90
(Summer 1989)
• Williamson, Ch 11.
Motivation
• Prior to RBC theory the mainstream idea was that
aggregate demand caused business cycles (e.g.
Keynesian IS-LM model)
• Can a dynamic competitive equilibrium (CE) model
provide an explanation of business cycles?
• In CE without investment, there is no persistence (HW
assignment #3)
• Investment provides a stronger link of economic
decisions over time.
• RBC model is the CE model with (i) shocks to
productivity and (ii) uncertainty and rational expectations.
• Real Business Cycle (RBC) theory originates
with:
(i) F. Kydland and E. Prescott
- 2004 Nobel Winners in Economics
- “Time to Build and Aggregate Fluctuations”
(Econometricia, 1982)
(ii) J. Long and C. Plosser
“Real Business Cycles” (Journal of Political
Economy, 1983)
• Productivity for the US economy can be
calculated using the Cobb-Douglas PF:
y = f(K,N) = zK0.3N0.7  z = y/K0.3N0.7
• Historically, the growth rate of productivity (z)
fluctuates with the business cycle.
Figure 4.20 The Solow Residual for
the United States
Figure 5.11 Deviations from Trend in Real
GDP and the Solow Residual
Table 3.1 The Production Function of
the United States, 1980–2004
8
• RBC model says that business cycles are
caused by temporary but persistent productivity
shocks:
zt 1  (1  r ) z  rzt   t 1
where 0 < r < 1 is degree of persistence.
• Productivity shocks are the impulse and
investment is the propagation mechanism.
• Rational Expectations: Households/Firms know
all variables up to time t and the random process
for z t and  t.
Numerical Example
• Consider t = 20 periods
• There is a one-time shock to t in period 1 where 1 = 10 and t = 0
for all other time periods:
10
e
t
10
5
0
0
0
0
5
10
t
15
20
20
• Notice the effect on zt depends on the value of r which measures
the amount of persistence for the shock .
22
20
r0
purely temporary
15
z
t
10
5
0
0
0
5
0
r  0.80 
10
15
t
20
20
22
20
temporary but
persistent
15
z
t
10
5
0
0
0
0
5
10
t
15
20
20
r  1  permanent
22
20
15
z
t
10
5
0
0
0
0
5
10
t
15
20
20
Timing
• Households & Firms are infinitely lived
• In each period t:
(i) Kt is known from last period.
zt shock is observed.
(ii) A rational expectation of zt+1 is formed.
(ii) Firms hire labor Ntd and buy capital Kt+1.
(cost of capital = rt + d)
(iii) Households supply labor Nts and consume ct.
(wages wt are paid)
(iv) Markets clear (labor, goods). Firm profits
paid to households.
Households
• In each period t households choose {ct+j,lt+j} to

max Et   j u(ct  j , lt  j )
j 0
subject to
  wt  j N ts j   t  j 
 
ct  j 
Et 
  Et 
j
j 
 j 0 (1  rt  j )

 j 0 (1  rt  j ) 
• FOC for Utility Maximization:
MRS ct ,ct 1
MRS l ,c
uc (ct , lt )

 (1  rt )
Et uc (ct 1 , lt 1 )
ul (ct , lt )

 wt
uc (ct , lt )
Firms
• In each period t firms choose {Ndt,Kt+1} to

max Et 
t j
j
(
1

r
)
j 0
t j
• FOC for Profit Maximization
f N ( K t , Nt )  wt
Et f K ( Kt 1 , Nt 1 )  rt  d
Market Clearing
• Goods
Y  yt  ct  I t  Y  zt F ( K t , N t )
s
d
• Labor
N  N  Nt
d
t
s
t
Social Planner
• Since solution to CE is Pareto Optimal it is equivalent
to the social planner’s problem:

max Et   t u(ct  j , lt  j )
ct , kt
j 0
subject to
ct  I t  yt  zt F ( Kt , Nt )
I t  Kt 1  (1  d ) Kt
Productivity Shocks
• Temporary Positive Shock
Supply 
higher ND and z shifts Ys
right. Decreases r* and shifts NS
left  N* ambiguous but increase
in w.
Demand 
Higher w increases c*  Yd shifts
right. No change in future MPK
 no (direct) effect on I.
Overall 
Increase in y* and decrease in r*
(C and I increases)
• There will be persistence: Higher I today 
Higher future output.
• Future Positive Shock
Supply 
Current z unchanged  Ys
fixed.
Demand 
Increases c* (from PIH) and
increase in I  Yd shifts
right.
Overall 
Increase in y* and increase in r*
Functional Forms
• Cobb-Douglas (log) Utility
u (c, l )  q ln( c)  (1  q ) ln( l )
Cobb-Douglas Technology
f ( K , N )  zF ( K , N )  zK a N 1a
where 0 < q < 1 and 0 < a < 1 are the elasticities
of substitution in utility and production functions.
• A CE is {ct,Nt,Kt+1} solving
q

a 1 a
 Et  [1  azt 1Kt 1 Nt 1  d ]
ct
 ct 1

q
1q
q
 zt (1  a ) K ta N ta
1  N t ct
ct  zt K ta N t1a  [ K t 1  (1  d ) K t ]
Special Case: d  1
• 100% depreciation  It = Kt+1
• Guess:
Nt = N constant
ct  1 yt  f1 zt Kta Nt1a
a
Kt 1  2 yt  f2 zt Kt N
1a
t
• “Method of Undetermined Coefficient” plug into
equilibrium conditions and verify guess by
solving for N, f1, and f2.
• Result:
(1  a )q
NN 
(1  a )(1  q )  (1  a )q
ct  (1  a ) yt
K t 1  I t  ayt
Predictions of Special Case
• Persistent Cycles in GDP
yt 1  zt 1 K ta1 N t11a  zt 1 (ayt )a N
• Volatility of C and I
MODEL
DATA
C,I procyclical
C,I procyclical
Var (ct) < Var (yt)
Var (ct) < Var (yt)
Var (It) < Var (yt)
Var (It) > Var (yt) (X)
Labor Market
Average Productivity: (yt/N) is procyclical,
Real Wages: wt = zFN(Kt,N) procyclical
• Real interest rate r is countercyclical.
• Problem: No fluctuations in N!
• Can be resolved by d < 1:
Substitution effect > income effect
Higher MPK magnifies productivity shock.
• No analytical solution. Need to use numerical
methods.
Form of Solution
• In each period t, the model’s state variables are: K t , z t
• Solution for each period t are functions of the model’s
state variables given K0 , z , and t:
zt 1  (1  r ) z  rzt   t 1
ct  c ( K t , z t )
N t  n( K t , z t )
K t 1  k ( K t , z t )
Effect of One Time Productivity Shock
Steps to Solving RBC Model
(1)
(2)
(3)
(4)
Solve for solutions of c(K,z), n(K,z),
k(K,z)
Calibrate Parameters: d = 0.25, a =
0.3,  = 0.99 (4% annual real interest
rate), persistence r = 0.8, ect.
Simulate Model to Generate Artificial
Data
Compare Artificial Economy with Real
Economy.
Figure 10.3 Small shocks and large cycles
GDP
Consumption
Investment
Employment
Performance of Real Business Cycle Models
Relative Volatility
Data
RBC
Corr with GDP
Data
RBC
C
0.46
0.31
0.78
0.98
I
2.91
3.15
0.71
0.99
N
0.82
0.49
0.82
0.98
(Y/N)
0.58
0.53
0.55
0.99
Corr(N,ω) 0.07
0.93
Variable
Compare with BC Facts
• Explains persistent fluctuations in Y, C, I.
• C and I are procyclical, C is less volatile than Y, I
more volatile than Y.
• N is procyclical but model still understates
volatility.
• Labor productivity (Y/N) is procyclical (too much)
• Price Level is countercyclical (?)
• Correlation between N and productivity (and w)
is close to one (too large).
Figure 11.3 Average Labor Productivity with
Total Factor Productivity Shocks
11-37
Table 11.1 Data Versus Predictions of the
Real Business Cycle Model with Productivity
Shocks
Hours-Wage Correlation
Shortcomings
• Still not enough volatility in N. Need
higher intertemporal substitution effect
relative to income effect.
• N and w correlation too large.
• Money is neutral.
Adding Government Spending
Shocks to RBC Model
• Firms:
yt  f ( Kt , N t )
f N ( Kt , N t )  w t
Et f K ( Kt 1 , Nt 1 )  rt  d
• Households:
 N twt   t  Tt 

ct 
E 
  E 
t
t 
(1  r )


 (1  r ) 
E ( MRS ct ,ct 1 )  1  rt
• Government BC:
and MRS l ,c  wt
t
G
/
(
1

r
)

 t
t
t
t
T
/
(
1

r
)
t
• Market-Clearing:
Labor:
Nd = Ns
Goods:
yt = Ct + It + Gt
Temporary DG
• Supply Side Effects
* Increase in G  Increase in T
* Small decrease in PDV of lifetime income
* Small shift of NS and Ys right
• Demand Side Effects
* Higher G  shifts Yd right by DG/(1-MPC).
* Higher T  small negative income effect
(consumption smoothing)  Yd left by
MPC*DT/(1-MPC).
* Since DT = DG, Shift Yd = DG
• Overall: Shift Yd > Shift Ys  Increase Y* and r*
 lower C and I
• Evidence:
(1) Procyclical G
(2) Wartime government spending and
Interest Rates
(3) G and I
The Growth Rate of U.S. Real Gross
Domestic Product since 1870
Figure 4.5 Gross and net investment,
1929–2002
Government Expenditures &
Investment
RBC Model w/ Government Spending
Shocks
Performance of Real Business Cycle Models
Variable
Data
Relative Volatility
RBC (difference)
C
0.46
0.31
(-0.15)
0.54
(0.08)
I
2.91
3.15
(0.24)
3.08
(0.17)
G
2.14
-----
2.0
(0.14)
N
0.82
0.49
(-0.33)
0.55
(-0.27)
(Y/N)
0.58
0.53
(-0.05)
0.61
(0.03)
0.07
0.93
(0.86)
0.49
(0.42)
Corr(N,ω)
Gov ( difference)
Hours-Wage Correlation
Hours-Wage Correlation
• Suggested Reading:
• G. Hansen and R. Wright
V. Li, “Can Market-Clearing Models Explain U.S.
Labor Market Fluctuations?” Economic Review,
Federal Reserve Bank of St. Louis (July 1999).
RBC Debate: Plosser vs
Mankiw
• Interpretation of Productivity Shocks (Solow Residuals)
*
Labor Hoarding
*
Aggregate Demand Shocks affect
Productivity
• Labor Supply Elasticity of Substitution
• Optimality of Business Cycles
- Stabilization policy
• Cyclical behavior of prices and neutrality of money
Shocks:
– Are prices pro or counter-cyclical?
– Phillips Curve trade-off
• Internal vs External Consistency