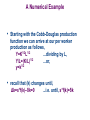Download The Solow Growth Model

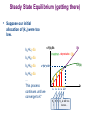
The Solow Growth
Model (Part One)
The steady state level of capital and
how savings affects output and
economic growth.
Model Background
• Previous models such as the closed economy and
small open economy models provide a static view
of the economy at a given point in time. The Solow
growth model allows us a dynamic view of how
savings affects the economy over time.
Building the Model: goods market supply
• We begin with a production function and assume constant
returns.
Y=F(K,L)
so… zY=F(zK,zL)
• By setting z=1/L we create a per worker function.
Y/L=F(K/L,1)
• So, output per worker is a function of capital per worker. We
write this as,
y=f(k)
Building the Model: goods market supply
• The slope of this function
•
is the marginal product
of capital per worker.
MPK = f(k+1)–f(k)
It tells us the change in
output per worker that
results when we increase
the capital per worker by
one.
y
MPK 
change in y
change in k
y=f(k)
Change in y
Change in k
k
Building the Model:
goods market demand
• We begin with per worker consumption and investment.
(Government purchases and net exports are not included in the
Solow model). This gives us the following per worker
national income accounting identity.
y = c+I
• Given a savings rate (s) and a consumption rate
(1–s) we can generate a consumption function.
c = (1–s)y
…which makes our identity,
y = (1–s)y + I …rearranging,
i = s*y
…so investment per worker
equals savings per worker.
Steady State Equilibrium
• The Solow model long run equilibrium occurs at the
point where both (y) and (k) are constant. These are
the endogenous variables in the model.
• The exogenous variable is (s).
Steady State Equilibrium
• By substituting f(k) for (y), the investment per worker
function (i = s*y) becomes a function of capital per worker
(i = s*f(k)).
• To augment the model we define a depreciation rate (δ).
• To see the impact of investment and depreciation on capital
we develop the following (change in capital) formula,
Δk = i – δk
…substituting for (i) gives us,
Δk = s*f(k) – δk
Steady State Equilibrium
•
If our initial allocation of (k)
were too high, (k) would
decrease because depreciation
exceeds investment.
•
s*f(k),δk
If our initial allocation were too
low, k would increase because
investment exceeds
depreciation.
s*f(k*)=δk*
•
•
At the point where both (k) and (y)
are constant it must be the case
that,
Δk = s*f(k) – δk = 0
…or,
s*f(k) = δk
…this occurs at our equilibrium
point k*.
At k* depreciation equals
investment.
klow
δk
s*f(k)
k*
khigh
k
Steady State Equilibrium (getting there)
• Suppose our initial
allocation of (k1) were too
low.
δk
s*f(k),δk
k2=k1+Δk
k3=k2+Δk
k4=k3+Δk
s*f(k)
s*f(k*)=δk*
k5=k4+Δk
…
This process
continues until we
converge to k*
k1
k2 k3 k4 k5 k*
K2 isKstill
is4still
too
K
is5still
is
too
still
tootoo
3K
low low
so…
low
so…
low
so…
so…
k
A Numerical Example
• Starting with the Cobb-Douglas production
function we can arrive at our per worker
production as follows,
Y=K1/2L1/2
…dividing by L,
Y/L=(K/L)1/2
…or,
y=k1/2
• recall that (k) changes until,
Δk=s*f(k)–δk=0
...i.e. until, s*f(k)=δk
A Numerical Example
• Given s, δ, and initial k, we can compute
time paths for our variables as we approach
the steady state.
• Let’s assume s=.4, δ=.09, and k=4.
• To solve for equilibrium set s*f(k)=δk. This
gives us .4*k1/2=.09*k. Simplifying gives us
k=19.7531, so k*=19.7531.
A Numerical Example
• But what it the time path toward k*? To get this
use the following algorithm for each period.
•
•
•
•
•
•
k=4, and y=k1/2 , so y=2.
c=(1–s)y, and s=.4, so c=.6y=1.2
i=s*y, so i=.8
δk =.09*4=.36
Δk=s*y–δk so Δk=.8–.36=.44
so k=4+.44=4.44 for the next period.
A Numerical Example
• Repeating the process gives…
period
k
y
c
i
δk
Δk
1
2
.
10
.
∞
4
4.44
.
8.343...
.
19.75...
2
2.107...
.
2.888...
.
4.44…
1.2
1.264...
.
1.689...
.
2.667...
.8
.842…
.
1.126...
.
1.777...
.36
.399…
.
.713…
.
1.777...
.44
.443…
.
.412…
.
0.000...
A Numerical Example
results
Paths of Variables
•20GraphingTime
our results in Mathematica gives us,
15
10
5
20
40
60
80
100
period
Changing the exogenous variable - savings
• We know that steady state
is at the point where
s*f(k)=δk
• What happens if we
δk
s*f(k),δk
s*f(k*)=δk*
s*f(k)
s*f(k)
s*f(k*)=δk*
increase savings?
• This would increase the
•
slope of our investment
function and cause the
function to shift up.
This would lead to a higher
steady state level of capital.
• Similarly a lower savings
rate leads to a lower steady
state level of capital.
k*
k**
k
Conclusion
• The Solow Growth model is a dynamic model that allows
us to see how our endogenous variables capital per
worker and output per worker are affected by the
exogenous variable savings. We also see how parameters
such as depreciation enter the model, and finally the
effects that initial capital allocations have on the time
paths toward equilibrium.
• In the next section we augment this model to include
changes in other exogenous variables; population and
technological growth.