Download No Slide Title

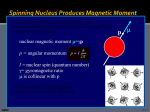
NMR excitation (detecting NMR)
• Last time we saw how an ensemble of spins (of a single type
and I = 1/2) generates an average magnetization, Mo, upon
interaction with an external magnetic field, Bo:
z
z
Mo
x
y
x
y
Bo
Bo
• We also saw that this magnetization is proportional to the
population difference of spins in the low and high energy
levels, and that it is precessing at a frequency wo, the Larmor
frequency of the particular observed spin at a particular Bo
• So far, nothing happened. We need to do something to the
system to observe any kind of signal. What we do is take it
away from this condition and observe how it goes back to
equilibrium. This means affecting the populations...
NMR excitation (continued)
• We need the system to absorb energy. The energy source
is an oscillating electromagnetic radiation generated by
an alternating current:
z
B1 = C * cos (wot)
Mo
x
B1
Bo
y
i
Transmitter coil (y)
• How is that something that has a linear variation can be
thought as circular field? A linear variation in y is the linear
combination of two counter-rotating circular fields:
y
y
y
-wo
x
=
x
+
+wo
x
For part of the period of oscillation:
=
+
=
+
• We go through zero and then it repeats…
=
+
• Only the one vector that rotates at +wo (in the same direction
of the precession of Mo) interacts with the bulk magnetization
Now we throw Mo on the mix
• When the frequency of the alternating current is wo, the
frequency of the right vector of B1 is wo and we achieve a
resonant condition. The alternating magnetic field and Mo
interact, there is a torque generated on Mo, and the
system absorbs energy :
z
Mo
B1
wo
z
x
B1 off…
x
Mxy
(or off-resonance)
y
y
wo
• Since the system absorbed energy, the equilibrium of the
system was altered. We modified the populations of the Na
and Nb energy levels.
• Again, keep in mind that individual spins flipped up or down
(a single quanta), but Mo can have a continuous variation.
Return of Mo to equilibrium (and detection)
• In the absence of the external B1, Mxy will try to go back to Mo
(equilibrium) by restoring the same Na / Nb distributiuon. We’ll
see the physics that rule this phenomenon (relaxation) later.
• Mxy returns to the z axis precessing on the <xy> plane (to
damm hard to draw…):
z
z
x
Mxy
Mo
equilibrium...
x
wo
y
y
• The oscillation of Mxy generates a fluctuating magnetic field
which can be used to generate a current in a coil:
z
x
Mxy
wo
y
Receiver coil (x)
 NMR signal
Laboratory and Rotating frames
• The coordinate system that we used for the previous example
(laboratory frame) is really pathetic. The whole system is
spinning at wo, which makes any kind of analysis impossible.
• Again, an out-of-date example. It would be like trying to read
the label of a long play spinning in a turn-table…
• The solution is to take a coordinate system that moves at wo.
This is like jumping on top of the long play to read the label.
What we effectively do is remove the effect of Bo. If we take
magnetization on the <xy> plane:
z
z
x
Bo
Mxy
y
x
wo
Laboratory Frame
Mxy
y
Rotating Frame
• In this coordinate system, Mxy does not move if we are at the
resonant condition (the w of B1 is exactly the frequency of the
nuclei, wo). If we are slightly off-resonance, the movement of
the vectors is still slow with respect to wo.
Chemical shifts
• If each type of nucleus has its characteristic wo at a certain
magnetic field, why is NMR useful?
• Depending on the chemical environment we have variations
on the magnetic field that the nuclei feels, even for the same
type of nuclei. It affects the local magnetic field.
Beff = Bo - Bloc --- Beff = Bo( 1 - s )
• s is the magnetic shielding of the nucleus. Factors that
affect it include neighboring atoms, aromatic groups, etc., etc.
The polarization of the bonds to the observed nuclei are
also important.
• As a crude example, ethanol looks like this:
HO-CH2-CH3
low
field
high
field
wo
The NMR scale (d, ppm)
• We can use the frequency scale as it is. The problem is that
since Bloc is a lot smaller than Bo, the range is very small
(hundreds of Hz) and the absolute value is very big (MHz).
• We use a relative scale, and refer all signals in the spectrum
to the signal of a particular compound.
d=
w - wref
wref
ppm (parts per million)
• The good thing is that since it is a relative scale, the d in a
100 MHz magnet (2.35 T) is the same as that obtained for
the same sample in a 600 MHz magnet (14.1 T).
• Tetramethyl silane (TMS) is used as
reference because it is soluble in most
organic solvents, is inert, volatile, and has
12 equivalent 1Hs and 4 equivalent 13Cs:
CH 3
H3C
Si
CH 3
CH 3
• Other references can be used, such as the residual solvent
peak, dioxane for 13C, or TSP in aqueous samples for 1H.
Scales for different nuclei
• For protons, ~ 15 ppm:
Acids
Aldehydes
Alcohols, protons a
to ketones
Aromatics
Amides
Olefins
Aliphatic
ppm
15
10
7
5
2
0
TMS
• For carbon, ~ 220 ppm:
C=O in
ketones
Aromatics,
conjugated alkenes
Olefins
Aliphatic CH3,
CH2, CH
ppm
210
150
C=O of Acids,
aldehydes, esters
100
80
50
0
TMS
Carbons adjacent to
alcohols, ketones
Chemical shift in the rotating frame
• We will consider only magnetization in the <xy> plane. We
start with a signal with an wo equal to the w of B1. After some
time passes, nothing changes…
y
y
Time (t)
x
x
• Now, if we are slightly off-resonance (w - wo  0), the Mxy
vector will evolve with time. The angle will be proportional to
the evolution time and w - wo (that’s why we use radians…)
y
y
Time (t)
x
f
w - wo
f = (w - wo) * t
x
Coupling Constants
• The energy levels of a nucleus will be affected by the spin
state of nuclei nearby. The two nuclei that show this are said
to be coupled to each other. This manifests in particular
in cases were we have through bond connectivity:
1
H
13
1
1
H
H
three-bond
C
one-bond
• Energy diagrams. Each spin now has two energy ‘sub-levels’
depending on the state of the spin it is coupled to:
I
bb
S
ab
J (Hz)
ba
S
I
aa
I
S
• The magnitude of the separation is called coupling constant
(J) and has units of Hz.
• Coupling patterns are crucial to identify spin systems in a
molecule and to the determination of its chemical structure.
Couplings in the rotating frame
• We will consider an ensemble of spins I coupled to another
spin S that is exactly at the resonant condition (w of B1 is wo),
and again, only what goes on in the <xy> plane.
• The situation is analogous to what happened with chemical
shift. In this case, since there are two new energy levels for
the spin, we get two counter-rotating vectors. Their evolution
will depend on the magnitude of J, not wo:
y
y
-J/2
t ...
x
x
t=1/J
+J/2
y
t=2/J
y
x
x
f=p*t*J
Take-home message…
a) Under the effect of chemical shifts, components of the total
magnetization of a sample will move faster or slower than
the reference frequency (i.e. the chemical reference, TMS).
b) Under the effect of scalar coupling, an ensemble of spins I
will separate in two counter rotating vectors at speeds of
+ and - J / 2. We have a p involved due to the Hz to radians
conversion.
c) The time we let the system evolve is extremely important.
By varying the evolution time we’ll be able to see different
things related to the sample.
Next class topics
• Instrumentation.
• Continuous Wave (CW) excitation.
• Pulses and Fourier Transformation.
• The free induction decay (FID).
• Data collection, processing, window functions, and
zero-filling.