Download File - Aerosona.Tec

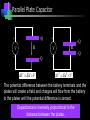
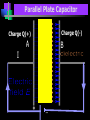
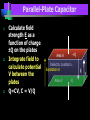
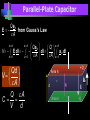
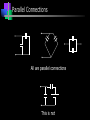
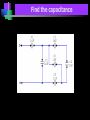
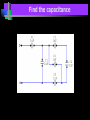
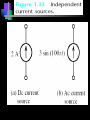
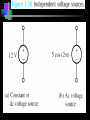
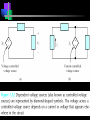
Capacitance
Basic Electrical Quantities
Capacitance
A capacitor is constructed of two parallel
conducting plates separated by an
insulator called dielectric
 The conducting surfaces can be
rectangular or circular
 The purpose of the capacitor is to store
electrical energy by electrostatic stress in
the dielectric
Some Capacitors
conductor
insulator
ELECTRICAL SCIENCE
Capacitance : Definition

Take two chunks of conductor




Separated by insulator
Apply a potential V between
them
Charge will appear on the
conductors, with Q+ = +CV on
the higher-potential and Q- = CV on the lower potential
conductor
C depends upon both the
“geometry” and the nature of the
material that is the insulator
Q+ = +CV
+++++++++++
+++++++++++
+++++++++++
ELECTRICAL SCIENCE
V
V
0
Parallel Plate Capacitor
When it is connected to a voltage
source, there is temporary flow of
electrons from plate A to plate B
 A capacitor has a capacitance of 1 farad
(F) if 1 coulomb (C) of charge is deposited
on the plates by a potential difference of 1
volt across its plates
 The farad is named after Michael Faraday,
a nineteenth century English chemist and
physicist
Capacitance
Capacitance is a measure of a capacitor’s
ability to store charge on its plates
 A capacitor has a capacitance of one farad
(F) if one coulomb (C) of charge is deposited
on the plates by a potential difference of one
volt across its plates
 The farad is named after Michael Faraday, a
nineteenth century English chemist and
physicist
Capacitance

Suppose we give Q coulomb of charge
to one of the two plates and if a P.D. of
V volts is established between the two
plates, then the capacitance is
Q
Charge
C 
V Potential Difference
 Hence, Capacitance is the charge
required per unit Potential Difference
Parallel Plate Capacitor
+Q
+
V
E
-
V
-Q
V  Ed  V
+
+Q
E
-Q
-
V   Ed   V
The potential difference between the battery terminals and the
plates will create a field and charges will flow from the battery
to the plates until the potential difference is zeroed.
Capacitance is inversely proportional to the
distance between the plates.
Capacitance
The farad is generally too large a
measure of capacitance for most practical
applications
 So microfarad (106 ) or picofarad
(1012 ) is more commonly used
 Different capacitors for the same voltage
across their plates will acquire greater or
lesser amounts of charge on their plates
 Hence, the capacitors have greater or
lesser capacitance
Parallel Plate Capacitor
Charge Q(-)
Charge Q(+)
A
B
I
+
_
Capacitance
 Dielectric – Insulator of the capacitor
 The purpose of the dielectric is to create
an electric field to oppose the electric field
setup by free charges on the parallel plates
 Di for “opposing” and electric for
“electric field”
Capacitance
With different dielectric materials
between the same two parallel plates,
different amounts of charge will deposit
on the plates
 Permittivity – The ratio of the flux
density to the electric field intensity in
the dielectric. A measure of how easily
the dielectric will “permit” the
establishment of flux lines within the
dielectric
Parallel-Plate Capacitor
1.
2.
3.
Calculate field
strength E as a
function of charge
±Q on the plates
Integrate field to
calculate potential
V between the
plates
Q=CV, C = V/Q
Area A
+Q
Dielectric constant e
Separation d
Area A
-Q
E
V
Parallel-Plate Capacitor
Qaz
E
from Gauss's Law
eA
 Qaz 
 Q  z d
V    E.dl     
 .dl  
  a z .dl
 e A  z 0
z 0
z 0  e A 
z d
z d
 Qd 
V 

 eA 
Q eA
C 
V
d
+Q
Area A
e
d
Area A
dl
âz
E
-Q
Capacitance in Series &
Parallel
Basic Electrical Quantities
Series Combination
V  V1  V2
Q  Q1  Q2
V1 
Q1 Q

C1 C1
V2 
Q2 Q

C2 C2
V 
Q
Q Q
 
Ceq C1 C2
1
1
1
 
Ceq C1 C2
For series capacitors
n
1
1

Ceq j 1 C j
Parallel Combination
Q  Q1  Q2
V  V1  V2
Q1  C1V1  C1V
Q2  C2 V2  C2 V
Q  Ceq V  C1V1  C2 V2
 C1V  C2 V
Ceq  C1  C2
For parallel capacitors Ceq 
n
C
j 1
j
Parallel Connections
All are parallel connections
This is not
Mixed Combination of Capacitors
Find the capacitance
Series and Parallel
Key ideas:
1.For capacitors in series, the charges are
all the same.
2.For capacitors in parallel, the potential
differences are all the same.
Mixed Combination of Capacitors
Find the capacitance
Inductance


Whenever a coil of wire is connected to a
battery through a rheostat and effort is
made to increase the current and hence
flux through it, it is always opposed by
the instantaneous production of counter
emf. The energy required to oppose this is
supplied by the battery
Similarly if the current is decreased then
again is delayed due to production of
counter emf
Inductance

This property of the coil due to which it
opposes any increase or decrease of
current or flux through it is known as
inductance or Self inductance
N
L=
I
where
N= turns in a coil
 = flux produced
I= current produced in a coil
If NΦ=1 Wb-turn and I= 1
ampere, then L= 1 Henry
Hence a coil is said to
have self-inductance of
one Henry if a current of
one ampere when flowing
through it produces flux
linkages of one Wb-turn in
it
Coefficient of Inductance




It is defined as the Weber-turns per
ampere in the coil
It is quantitatively measured in terms of
coefficient of self induction
Symbol (L), Unit H (Henry)
The property is analogous to inertia in a
material body
Electrical Energy
Sources
Classification of Sources




Voltage Source
Current Source
Further sub classified as


Ideal or Non-ideal
Dependent or Independent
Voltage Source

An ideal voltage
source is a source of
voltage with zero
internal resistance
(a perfect battery)

Supply the same
voltage regardless of
the amount of
current drawn from
it
Voltage Source


An non-ideal or real
or practical voltage
source has a small
but finite resistance
The terminal voltage
delivered is less by
an amount equaling
the voltage drop
caused by the
internal resistance
EAB  Es  ir
If r=0, then
the source
becomes Ideal
Voltage Source
Independent Voltage Source


An ideal voltage source is shown
to be connected to an arbitrary
network
The defining equation is
vt (t )  vs (t ) for any i(t )



The voltage source is completely
specified by its voltage for all t
It does not depend on the
connected network in any
manner
Such ideal voltage source is also
called an Independent Voltage
source
i(t) +
+
vs(t)
v(t)
-
-
Arbitrary
Network


Current Source
An ideal current source
is capable of producing
a specified current
through it regardless of
what is connected to it
The current supplied is
independent of the
voltage at the source
terminals
Current Source

An non-ideal or real
or practical current
source has a large
but finite resistance
E AB
i  Is 
R
If r=infinite,
then the
source
becomes Ideal
current Source
Independent Current Source


An ideal current source is shown
to be connected to an arbitrary
network
The defining equation is
i(t) +
i(t )  is (t ) for any v(t )



The current source is completely
specified by its current is(t) for
all t
It does not depend on the
connected network in any
manner
Such ideal current source is also
called an Independent current
source
+
is(t)
v(t)
-
-
Arbitrary
Network