Download Oscillators_PartB (Chp 5)

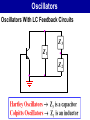
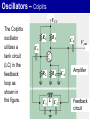
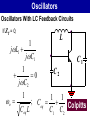
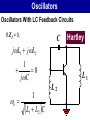
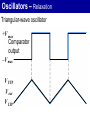
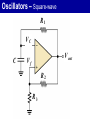
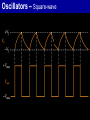
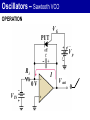
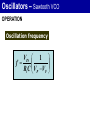
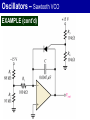
Oscillators
2. LC Oscillators
Oscillators
Oscillators With LC Feedback Circuits
For frequencies above 1 MHz, LC feedback
oscillators are used.
We will discuss the Colpitts, Hartley and
crystal-controlled oscillators.
Transistors are used as the active device in
these types.
Oscillators
Oscillators With LC Feedback Circuits
Z3
Z1
Z2
Oscillators – Colpitts
V CC
The Colpitts
oscillator
utilizes a
tank circuit
(LC) in the
feedback
loop as
shown in
the figure.
R1
R3
C5
V out
C3
R2
R4
C1 L C2
C4
Amplifier
Feedback
circuit
Oscillators – Colpitts
LC feedback oscillators use resonant circuits in the feedback path.
A popular LC oscillator is the Colpitts oscillator. It uses two
series capacitors in the resonant circuit. The feedback voltage is
developed across C1.
Vf
The effect is that the tank
circuit is “tapped”.
Usually C1 is the larger
capacitor because it
develops the smaller
voltage.
Av
Vout
L
Out
In
I
C1
C2
Vf
Vout
Oscillators
Oscillators With LC Feedback Circuits
If ZT = 0;
1
jL1 
jC1
L
C1
1
C
2

0
jC2
1
1
1
o 
; Ceq 

Colpitts
Ceq L
C1 C2
Oscillators – Colpitts
Total capacitance (CT ) is ;
1
1
1


CT C1 C2
CT 
C1C 2
C1  C 2
The resonant frequency can be determined by the formula below.
1
fr 
2 LCT
Oscillators – Colpitts
Conditions for oscillation and start up

Vf
Vf
Vout
Av
IX c1 C2


IX c 2 C1
1
C1
Av  
 C2
V out
L
Out C 1
Vf
I
C2
V out
In
Oscillators – Colpitts
If Q > 10, this formula gives good results.
Recall that the total capacitance of two series capacitors is the
product-over-sum of the individual capacitors. Therefore,
fr 
1
 CC 
2π L  1 2 
 C1  C2 
Zin
Vout
For Q < 10, a correction for Q is
L
1
fr 
2π LCT
Q2
Q2  1
C1
C2
Oscillators – Hartley
V CC
The Hartley
oscillator is similar
to the Colpitts.
The tank circuit
has two inductors
and one capacitor
R1
R3 C
2
C1
C4
V out
R2
R4
L1 C5 L2
C3
Amplifier
Feedback
circuit
Oscillators – Hartley
The Hartley oscillator is similar to the Colpitts oscillator,
except the resonant circuit consists of two series
inductors (or a single tapped inductor) and a parallel
capacitor. The frequency for Q > 10 is
1
fr 

2π LTC 2π
One advantage of a
Hartley oscillator is
that it can be tuned
by using a variable
capacitor
in
the
resonant circuit.
1
 L1  L2  C
Vf
Vout
Av
C
Out
L1
L2
In
Oscillators
Oscillators With LC Feedback Circuits
If ZT = 0;
C
Hartley
jL1  jL2
1

0
j C
1
o 
L1  L2 C
L1
L2
Oscillators – Hartley
The calculation of the resonant frequency is the same.
1
fr 
2 LT C
L1

L2
LT  L1  L2
1
L2
Av  
 L1
Oscillators – Crystal
The crystal-controlled oscillator is the most stable and
accurate of all oscillators. A crystal has a natural
frequency of resonance. Quartz material can be cut or
shaped to have a certain frequency.
Quartz
wafer
XTAL
Cm
Ls
Cs
Rs
(a) Typical
packaged
crystal
(b) Basic
(b) Symbol
construction
(without case)
(b) Electrical
equivalent
Oscillators – Crystal
V CC
Since crystal has
natural resonant
frequencies of 20 MHz
or less, generation of
higher frequencies is
attained by operating
the crystal in what is
called the overtone
mode
R1
R3
C2
V out
R2
R4
XTAL C C
C1
Oscillators
3. Relaxation Oscillators
Oscillators – Relaxation
Relaxation oscillators make use of an RC timing
and a device that changes states to generate a
periodic waveform (non-sinusoidal).
1. Triangular-wave
2. Square-wave
3. Sawtooth
Oscillators – Relaxation
Triangular-wave oscillator
Triangular-wave oscillator circuit is a combination
of a comparator and integrator circuit.
Comparator
A square wave
can be taken
as an output
here.
C
R1
V out
R2
Integrator
R3
Oscillators – Relaxation
Triangular-wave oscillator
+V max
Comparator
output
-V max
V UTP
V out
V LTP
Oscillators – Relaxation
Triangular-wave oscillator
1  R2 
 
fr 
4CR1  R3 
VUTP
 R3 
 Vmax  
 R2 
VLTP
 R3 
 -Vmax  
 R2 
Oscillators – Relaxation
For the triangular wave generator, the frequency is found from:
1  R2 
fr 
 
4 R 1 C  R3 
What is the frequency of the circuit shown here?
fr 

1  R2 
 
4 R 1 C  R3 
1
 22 kW 


4  82 kW 10 nF   10 kW 
C
–
R1
82 kW
+
Comparator
R2
22 kW
R3
= 671 Hz
10
– nF
10 kW
Vout
+
Integrator
Oscillators – Relaxation
Normally, the triangle wave generator uses fast comparators to
avoid slew rate problems. For non-critical applications, a 741 will
work nicely for low frequencies (<2 kHz). The circuit here is one
you can construct easily in lab. (The circuit is the same as Example
16-4 but with a larger C.)
The waveforms
are:
Vout2
C
Square wave
–
741
+
–
10 kW
R2
33 kW
R3
Both channels: 5 V/div
250 ms/div
0.1 mF
R1
10 kW
741
+
Vout1
Triangle
wave
Oscillators – Square-wave
A square wave relaxation oscillator is like the
Schmitt trigger or Comparator circuit.
The charging and discharging of the capacitor
cause the op-amp to switch states rapidly and
produce a square wave.
The RC time constant determines the frequency.
Oscillators – Square-wave
R1
VC
C
V out
Vf
R2
R3
Oscillators – Square-wave
Oscillators – Sawtooth voltage controlled
oscillator (VCO)
Sawtooth VCO circuit
is a combination of a
Programmable
Unijunction Transistor
(PUT) and integrator
circuit.
Ri
VG
PUT
Vp
-
I
0V
V IN
+
V out
Oscillators – Sawtooth VCO
OPERATION
Initially, dc input = -VIN
• Vout = 0V, Vanode < VG
• The circuit is like an integrator.
• Capacitor is charging.
• Output is increasing positive going ramp.
Oscillators – Sawtooth VCO
OPERATION
VG
PUT
Vp
-
Ri
I
0V
V IN
+
V out
0
Oscillators – Sawtooth VCO
OPERATION
When Vout = VP
•
•
Vanode > VG , PUT turns ‘ON’
The capacitor rapidly
discharges.
•
Vout drop until Vout = VF.
•
Vanode < VG , PUT turns ‘OFF’
VP – maximum peak value
VF – minimum peak value
Oscillators – Sawtooth VCO
OPERATION
Oscillation frequency
VIN  1 


f 
Ri C  VP - VF 
Oscillators – Sawtooth VCO
EXAMPLE
In the following circuit, let VF = 1V.
a) Find;
(i) amplitude;
(ii) frequency;
b) Sketch the output waveform
Oscillators – Sawtooth VCO
EXAMPLE (cont’d)
Oscillators – Sawtooth VCO
EXAMPLE – Solution
a) (i) Amplitude
R4
10
 V  
15  7.5 V
VG 
R3  R4
10  10
VP  VG  7.5 V
and
So, the peak-to-peak amplitude is;
VP - VF  7.5 -1  6.5 V
VF  1 V
Oscillators – Sawtooth VCO
EXAMPLE – Solution
a) (ii) Frequency
VIN  1

f 
Ri C  VP - VF



R2
- V   -1.92 V
VIN 
R1  R2
Oscillators – Sawtooth VCO
EXAMPLE – Solution
a) (ii) Frequency
1.92
1


f 


100k 0.0047μ   7.5V - 1V 
 628 Hz
Oscillators – Sawtooth VCO
EXAMPLE – Solution
b) Output waveform
1
1
T 
 2 ms
f 628
7.5 V
V out
1V
2 ms
t
Oscillators
The 555 timer
as an oscillator
Oscillators
The 555 Timer As An Oscillator
The 555 timer is an integrated circuit that can be
used in many applications. The frequency of
output is determined by the external components
R1, R2, and C. The formula below shows the
relationship.
144
fr 
R1  2 R2 Cext
Oscillators
The 555 Timer As An Oscillator
Duty cycles can be adjusted by values of R1 and
R2. The duty cycle is limited to 50% with this
arrangement. To have duty cycles less than 50%,
a diode is placed across R2. The two formulas
show the relationship;
Duty Cycle > 50 %
 R1  R2 
100%
Duty cycle  
 R1  2 R2 
Oscillators
The 555 Timer As An Oscillator
Duty Cycle < 50 %
 R1 
100%
Duty cycle  
 R1  R2 
Oscillators
The 555 Timer As An Oscillator
Oscillators
The 555 Timer As An Oscillator
The 555 timer
may be
operated as a
VCO with a
control voltage
applied to the
CONT input
(pin 5).
Oscillators
Summary
 Sinusoidal oscillators operate with positive
feedback.
 Two conditions for oscillation are 0º feedback
phase shift and feedback loop gain of 1.
 The initial startup requires the gain to be
momentarily greater than 1.
 RC oscillators include the Wien-bridge, phase
shift, and twin-T.
 LC oscillators include the Colpitts, Clapp, Hartley,
Armstrong, and crystal.
Oscillators
Summary (cont’d)
 The crystal actually uses a crystal as the LC tank
circuit and is very stable and accurate.
 A voltage controlled oscillator’s (VCO) frequency
is controlled by a dc control voltage.
 A 555 timer is a versatile integrated circuit that can
be used as a square wave oscillator or pulse
generator.
END CHAPTER 5