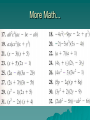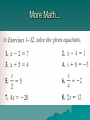Download Sound

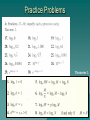
Acoustics
Week 1:
*Fundamentals of Sound
*Sound Levels and the
Decibel
Fundamentals of Sound




Sound can be defined as a wave motion in air or other elastic
media (stimulus) or as that excitation of the hearing
mechanism that results in the perception of sound (sensation).
Frequency is a characteristic of periodic waves measured in
hertz (cycles per second), readable on an oscilloscope or
frequency counter. The ear perceives a different pitch for a
quiet tone than a loud one. The pitch of a low-frequency tone
goes down, while the pitch of a high-frequency tone goes up
as intensity increases. We cannot equate frequency and pitch,
but they are analogous.
The same situation exists between intensity and loudness.
The relationship between the two is not linear.
Similarly, the relationship between waveform (or spectrum)
and perceived quality (or timbre) is complicated by the
functioning of the hearing mechanism.
Sine Waves

The sine wave is a
basic waveform
closely related to
simple harmonic
motion. Vibration
or oscillation is
possible because of
the elasticity of the
spring and the
inertia of the
weight. Elasticity
and inertia are two
things all media
must possess to be
capable of
conducting sound.
Sine Wave Language

The easiest value to read
is the peak-to-peak value
(of voltage, current, sound
pressure, etc.). If the
wave is symmetrical, the
peak-to-peak value is
twice the peak value.
Another common way to
measure the sine wave is
using RMS (Root Mean
Square) values. The other
two scales of
measurement used are
peak and average. The
picture to the right shows
four different ways that a
sine wave’s amplitude can
be measured and the
equations used for
conversions.
Propagation of Sound




If an air particle is displaced from its
original position, elastic forces of the
air tend to restore it to its original
position. Because of the inertia of the
particle, it overshoots the resting
position.
Sound is readily conducted in gases,
liquids, and solids such as air, water,
steel, etc., which are all elastic
media.
Without a medium, sound cannot be
propagated. Outer space is an almost
perfect vacuum; no sound can be
conducted due to the absence of air.
Particles of air propagating a sound
wave do not move far from their
undisplaced positions.
Forms of Particle Motion


There is more
than a million
molecules in a
cubic inch of air.
The molecules
crowded together
represent areas of
compression and
the sparse areas
represent
rarefactions.
Sound in Free Space



The intensity of sound
decreases as the
distance to the source is
increased.
Doubling the distance
reduces the intensity to
1/4 the initial value,
tripling the distance
yields 1/9, increasing
the distance four times
yields 1/16 the initial
intensity.
The inverse square
law states that the
intensity of sound in a
free field is inversely
proportional to the
square of the distance
from the source.
Wavelength, Period, & Frequency

The wavelength is the distance a wave travels in the
time it takes to complete one cycle. The period is the
time it takes a wave to complete one cycle. The
frequency is the number of cycles per second (Hertz).
Wavelength and Frequency
Formulas for calculating wavelength
and frequency. The speed of sound in
air is about 1,130 feet per second at
normal temperature and pressure.
Two graphical approaches for an easy
solution to the above equations.
Complex Waves

The sine wave with
the lowest frequency
(f1) is called the
fundamental, the one
with twice the
frequency (f2) is called
the second harmonic,
and the one three
times the frequency
(f3) is the third
harmonic. Harmonics
are whole number
multiples of the
fundamental
frequency.
Phase

Phase is the
time
relationship
between
waveforms.
Each waveform
is lagging the
previous by 90
degrees.
Combinations of Waveforms

Combinations of
waveforms that are
not in phase. The
difference in
waveshapes is due
entirely to the
shifting of the
phase of the
harmonics with
respect to the
fundamental.
Harmonics and Octaves
Spectrum


The audio or frequency
spectrum of the human
ear is about 20 Hz to
20 kHz. The spectrum
tells how the energy of
the signal is distributed
in frequency. For the
ideal sine wave, all the
energy is concentrated
at one frequency. All
other types of
waveforms have more
than one frequency
present.
The diagram shows
various types of
waveforms and their
harmonic content. The
sine, triangle, and
square waves are
known as period
waves due to their
cyclic pattern.
Sound Levels and the Decibel



Levels in decibels make it easy to handle the extremely wide
range of sensitivity in human hearing.
The threshold of hearing matches the ultimate lower limit of
perceptible sound in air.
A level in decibels is a convenient way of handling the billion
fold range of sound pressures to which the ear is sensitive
without getting bogged down in a long string of zeros.
Ratios vs. Difference




Ratios of pressure seem to describe loudness changes
better than difference in pressure.
Ernst Weber (1834), Gustaf Fechner (1860), Hermann
von Helmholtz (1873), and other researchers pointed
out the importance of ratios.
Ratios of stimuli come closer to matching up with
human perception than do differences of stimuli.
Ratios of powers, intensities, sound pressure, voltage,
or anything else are unitless. This is important
because logarithms can be taken only of unitless
numbers.
Handling Numbers

Here are three different ways that numbers can be expressed
Handling Numbers, cont’d.
Back to Basics: Math

The study of acoustics requires a knowledge of some basic algebra.
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
More Math...
Exponents: A Review
Exponents, cont’d.
Exponents, cont’d.
Exponents, cont’d.
Exponents, cont’d.
Exponents, cont’d.
Exponents, cont’d.
Exponents, cont’d.
Practice Problems
Logarithms
Logarithms
Logarithms
Practice Problems
Practice Problems
Theorem 1
Decibels


A level is a logarithm of a ratio of two like-power
quantities.
A level in decibels is ten times the logarithm to
the base 10 of the ratio of two power quantities.
Decibels


Sound pressure is proportional to (sound power)2.
The squaring of the sound power results in the
equation SPL = 20 log (p1/p2) instead of 10 log.
Sound Pressure Level (SPL)

Sound pressure
is usually the
most accessible
parameter to
measure in
acoustics, as
voltage is for
electronic
circuits. For this
reason, the
Equation (2-3)
form is more
often
encountered in
day-to-day
technical work.
Reference Levels


A sound level meter is used to
read sound pressure levels. A
sound level meter reading is a
certain sound pressure level, 20
log (p1/p2). For sound in air, the
standard reference pressure is
20 μPa (micropascal). The μPa is
a very minute sound pressure
and corresponds closely to the
threshold of human hearing.
The equations to the right show
how to convert SPL (in dB) to
μPa.
Log-to-Exponent Conversion

Here’s another
quick look at the
math used to
convert logs to
exponents:
Acoustic Reference Levels
Acoustic Reference Levels

Greek prefixes
used for the
powers of 10:
Pascals vs. Decibels


Doubling of acoustic
power is an increase
of 3 dB (10 log 2 =
3.01).
Doubling of acoustic
pressure is an
increase of 6 dB (20
log 2 = 6.02)
Pascals vs. Decibels
Decibel Level Examples

Here are some examples of decibel level
conversions:
Decibel Level Examples
Examples, cont’d.
Examples, cont’d.
Reflected Sound

The equations below show how to calculate
Reflection Delay and Reflection Level.
Examples, cont’d.
Examples, cont’d.
Examples, cont’d.
Ratios and Octaves

An octave is defined as a 2:1 ratio of two
frequencies. The ratio 3:2 is a fifth and 4:3 is a
fourth.
Examples
Examples, cont’d.
Measuring Sound Pressure Level

Sound level meters usually offer a selection of weighting networks
designated A, B, and C. Network selection is based on the general level of
sounds to be measured. For SPLs of 20 – 55 dB, use network A. For 55 –
85 dB use network B, and for 85 – 140 dB, use network C.
Equal Loudness Contours
The Precedence (Haas) Effect
SPL Changes With Distance

The Inverse
Square Law
says that
the intensity
of sound is
inversely
proportional
to the
square of
the distance
from the
point
source.
Inverse Distance Law

The Inverse
Square Law of
intensity
becomes the
Inverse
Distance Law
for sound
pressure.
Sound
pressure level
is reduced 6
dB for each
doubling of
distance.
Critical Distance

The Critical
Distance is
that
distance at
which the
direct sound
pressure is
equal to the
reverberant
sound
pressure.