Download Digital Systems: Hardware Organization and Design

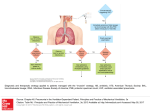
Signal and Systems
Introduction to Signals and
Systems
Introduction to Signals and
Systems
 Introduction to Signals and
Systems as related to Engineering
 Modeling of physical signals by
mathematical functions
 Modeling physical systems by
mathematical equations
 Solving mathematical equations
when excited by the input
functions/signals.
23 May 2017
Veton Këpuska
2
Modeling
 Engineers model two distinct physical
phenomena:
1. Signals are modeled by mathematical
functions.
2. Physical systems are modeled by
mathematical equations.
23 May 2017
Veton Këpuska
3
What are Signals?
23 May 2017
Veton Këpuska
4
Signals
 Signals, x(t), are typically real
functions of one independent variable
that typically represents time; t.
 Time t can assume all real values:
-∞ < t < ∞,
 Function x(t) is typically a real
function.
23 May 2017
Veton Këpuska
5
Example of Signals: Speech
23 May 2017
Veton Këpuska
6
Example of Signals EKG:
23 May 2017
Veton Këpuska
7
Example of Signals: EEC
23 May 2017
Veton Këpuska
8
Categories of Signals
 Signals can be:
1. Continuous, or
2. Discrete:



23 May 2017
T – sampling rate
f – sampling
frequency – 1/T
 – radial
sampling
frequency – 2f=
2/T
Veton Këpuska
9
Signal Processing
 Signals are often
corrupted by noise.
s(t) = x(t)+n(t)
Deterministic
signal
 Want to ‘filter’ the
measured signal s(t) to
remove undesired noise
effects n(t).
 Need to retrieve x(t).
Corrupting,
stochastic
noise signal
Signal Processing
23 May 2017
Veton Këpuska
10
What is a System?
23 May 2017
Veton Këpuska
11
Modeling Examples
 Human Speech Production is driven
by air (input signal) and produces
sound/speech (output signal)
 Voltage (signal) of a RLC circuit
 Music (signal) produced by a musical
instrument
 Radio (system) converts radio
frequency (input signal) to sound
(output signal)
23 May 2017
Veton Këpuska
12
Speech Production
 Human vocal tract as a system:
 Driven by air (as input signal)
 Produces Sound/Speech (as output signal)
 It is modeled by Vocal tract transfer
function:
 Wave equations,
 Sound propagation in a uniform acoustic tube
 Representing the vocal tract with simple
acoustic tubes
 Representing the vocal tract with multiple
uniform tubes
23 May 2017
Veton Këpuska
13
Anatomical Structures for
Speech Production
23 May 2017
Veton Këpuska
14
Uniform Tube Model
cos   l  x  c 
u  x, t  
U g    e jt
cos   l c 
 c sin   l  x  c 
p  x, t   j
U g    e jt
A
cos   l c 
 Volume velocity, denoted as u(x,t), is defined as the
rate of flow of air particles perpendicularly through a
specified area.
 Pressure, denoted as p(x,t), and
u(0, t )  U g ()e
23 May 2017
Veton Këpuska
jt
15
RLC Circuit
L
R
i(t)
C
v(t)
t
di (t )
1
L
 Ri (t )   i ( )d  v(t )
dt
C 





Voltage, v(t) input signal
Current, i(t) output signal
Inductance, L (parameter of the system)
Resistance, R (parameter of the system)
Capacitance, C (parameter of the system)
23 May 2017
Veton Këpuska
16
Newton’s Second Law in Physics
2
d x(t )
f (t )  M
dt 2
 The above equation is the model of a
physical system that relates an object’s
motion: x(t), object’s mass: M with a force
f(t) applied to it:
 f(t), and x(t) are models of physical signals.
 The equation is the model of the physical
system.
23 May 2017
Veton Këpuska
17
What is a System?
 A system can be a collection of
interconnected components:
 Physical Devices and/or
 Processors
 We typically think of a system as
having terminals for access to the
system:
 Inputs and
 Outputs
23 May 2017
Veton Këpuska
18
Example:
 Single Input/Single Output (SISO) System
Electrical
Network
Vin
+
Vout
-
+
-
 Multiple Input/Multiple Output (MIMO) System
x1 (t)
x2 (t)
System
…
…
xp (t)
23 May 2017
y1 (t)
y2 (t)
yp (t)
Veton Këpuska
19
Example:
 Alternate Block Diagram Representation of a
Multiple Input/Multiple Output (MIMO) System
x(t)
System
 x1 t  
 x t 
2


xt  
  


 x p t  p1
23 May 2017
y(t)
 y1 t 
 y t 
2


y t  
  


 yq t 
Veton Këpuska
q1
20
System Modeling
Physical
System
Mathematical
Model
Model
Analysis
Design
Procedure
Model
Simulation
23 May 2017
Veton Këpuska
21
Model Types
1. Input-Output Description
 Frequency-Domain Representations:
 Transfer Function - Typically used on ideal
Linear-Time-Invariant Systems
 Fourier Transform Representation
 Time-Domain Representations
 Differential/Difference Equations
 Convolution Models
2. State-Space Description
 Time-Domain Representation
23 May 2017
Veton Këpuska
22
Model Types
1. Continuous Models
2. Discrete Models
23 May 2017
Veton Këpuska
23
End
23 May 2017
Veton Këpuska
24