Download Course description

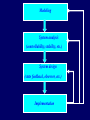
Linear System Theory
Instructor: Zhenhua Li
Associate Professor
[email protected]
Mobile：18660166181
School of Control Science and Engineering, Shandong University
Course description
Electric Motor

Computer
Amplifier
Voltage
This course is about control
An example: Control an electric motor
We want to spin a motor at a given angular
velocity. We can apply a fixed voltage to it, and
never check to see if it is rotating properly.
Called open loop. Power
Electric
Motor
Angular
Velocity
Course description
What if there is a changing load on the motor?
– Our output velocity will change!
speed w
no torque at max speed
torque t
stall torque
Course description
Closing the loop
Let’s measure the actual angular velocities.
Now we can compensate for changes in load by
Computer
Power
Amplifier
Voltage
feeding back some information.
Electric
Motor
Tachometer
Angular
Velocity
Course description
Classic Feedback Diagram
Command
input
x(t)
Error
e(t)
External
Disturbance
d(t)
Actuator
command
u(t)
Controller
Power
Amplification
Sensor
Reading
b(t)
Sensor
Actuator
or
Plant
System
ouput
y(t)
Course description
Laplace Transform of Classic
Feedback System
Command
input
X(s)
Error
E(s)
Controller
C(s)
Actuator
command
U(s)
External
Disturbance
D(s)
Actuator
A(s)
Sensor
Reading
B(s)
Sensor
S(s)
System
ouput
Y(s)
Course description
This course is the Transition from classical control to
modern control
by introducing the notion of state space
Linear control systems
Linear system theory
Nonlinear control
Robust control
Optimal control
Adaptive control
Course organization
Time: Wednesday 2:00 pm−3:50 pm
 Instructor: Dr. Zhenhua Li
– (Office)
– (Email) [email protected]
– (Phone) 18660166181
– (Office hours) Tuesday 4 pm−7 pm;
visits at other times are also welcome

Course organization
Time: Wednesday 2:00 pm−3:50 pm
 Instructor: Dr. Zhenhua Li
 Text book
– Chi-Tsong Chen, Linear System Theory and Design, 3rd
Edition, Oxford University Press, Oxford, UK, 1999.
 Lecture notes
– http://www.???
 Email list
– Important or emergent notice will be sent to you via emails
– Please provide me an email address that is most convenient
with you

Course organization






Time: Wednesday 5:20 pm-7:50 pm
Instructor: Dr. Zhi-Hong Mao
Text book
Lecture notes
Email list
Course evaluation
– Homework and class participation: 30% (late
homework will not be accepted)
– Final exam: 70%
Contents
Chapter 1 Mathematical Descriptions of Systems
Chapter 2 Controllability and Observability of
Linear Dynamical Equations
Chapter 3 Canonical Form and Irreducible Realization of
Linear Time-invariant Systems
Chapter 4 Pole Placement and Decoupling by
State Feedback
Chapter 5 Static Output Feedback and Estimators
Chapter 6 Stability Analysis of Linear Systems
Introduction
I. Control System Design Steps
The design of the controller that can alter or modify
the behavior and response of a plant to meet certain
performance required can be a tedious and challenging
problem. “Plant” here means any process characterized
by a certain number of inputs u and outputs yc, as
shown below.
u
yc
For example, we consider the following physical system,
which is usually complex, i.e., it may consist of various of
mechanical, electronic, hydraulic parts, etc. The design
of u is in general not a straightforward work, because the
plant process is usually complex.
If we know nothing about the system, what we can do is
to take a series of typical input signals and observe its
corresponding outputs. For instance,
u
yc
t
t
t
u
yc
t
Thought the physical system may be very complex, from
the above responses, the system can be described
approximately by the following first-order system:
dyc
1
T
 a yc  u  Y c (s ) 
U (s )
dt
Ts a
If the system does not meet our requirements, the
traditional way is to design a compensator, or a feedback
or simply adjust the parameter of the system. This design
method has been successfully applied to controller design
of many systems.
However, if a high performance is required for a system,
the above-mentioned traditional design method may not
give satisfactory results. Consequently, the internal states
of the system should be analyzed, that is, the state-space
description should be considered.
The following control steps are often followed by most
control engineers in designing the control law u.
Step 1. Modeling
The task of control engineer in this step is to understand
the processing mechanism of the plant. By taking a given
input signal u(t) and measuring the output response y(t),
he or she can describe the plant in the form of some
mathematical equations. These equations constitute the
mathematical model of the plant.
Step 2. System Analysis based on the Model
The analysis is twofold: qualitative analysis and
quantitative analysis. Qualitative analysis includes
stability, controllability and observability, etc., while
the quantitative analysis needs to compute the response
with the help of a computer.
Step 3. Controller Design based on the model
If the system cannot achieve the asked performance,
we have to design a controller or change the control low.
Generally speaking, system controller design is a more
complex issue.
Step 4. Implementation
In this step, a controller designed in Step 3, which is
shown to meet the performance requirements for the
plant model and is robust with respect to possible
plant model uncertainties, is ready to be applied to the
unknown plant.
Another important aspect of implementation is the
final adjustment, or as often called the tuning, of the
controller to improve performance by compensating
for the plant model uncertainties that are not
accounted for during the design process.
Modeling
System analysis
(controllability, stability, etc.)
System design
(state feedback, observer, etc.)
Implementation
II. Linear systems
Many physical systems can be treated as linear systems
with finite dimension at their operating points due to the
following reasons:
1. Linear systems can be handled by using some
powerful mathematical tools;
2. Linear systems in most cases can faithfully describe
the behavior of the controlled plants.
As a matter of fact, linear system theory is the cornerstone
of modern control theory.