Download Lecture 7: High-level power reduction and management

High-level Power Reduction and
Management
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
2
General Observations
 Not all components need to be active all the time
 Energy-efficient computations achieved by selectively turning off
(or reducing the performance of) system components when they
are idle
 Issues:
■ Controls to support power management
● Frequency control (clock gating)
● Voltage control (power shutdown)
■ Identify when circuits (or parts) can be idle
■ Location of controls
● Hardware
● Software (Hybrid)
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
3
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
4
Gated Clock Architecture
 Block Fa is controlled by primary inputs, state, and primary
outputs
STATE
Combinational
Logic
IN
OUT
GCLK
fa
L
&
CLK
 Latch L takes care of filtering glitches
■ L is transparent when clock is inactive
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
5
Gated Clock Architecture : Redundant Clocking
Detection
 Idea [Ohnishi97]:
■ Redundant clockings activate registers unnecessarily
■ Use application profiles to detect redundant clockings
● Difference in the numbers of incoming and outgoing data of a
register
■ Gated clock scheme designed using this information
 Redundant behaviors of a register
■ Unused data latching: Data not transferred to a destination
■ Unchanged data latching: Register re-stores data already present
from source
■ Redundant data holding: Register re-stores data already present
from itself.
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
6
Redundant Clocking Detection
 Identify the redundant behaviors for register X during the 10
clock cycle snapshot shown.
Courtesy: [Ohnishi97]
 # Unused data latching(X) or
AUU (X )
= 8-6=2
 # Unchanged data latching(X) or AUC ( X ) = 8 - 5 = 3
 # Redundant data holding(X) or AHOLD (X ) = 10 – 8 = 2
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
7
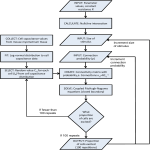
Algorithm
 Algorithm for redundant clocking detection and gated clock
architecture definition
1. Register data transfer condition extraction
● Analyze RTL HDL of circuit to extract data transfer
conditions
● Conditions under which data transfers to/from register
happened
2. Profiling
● Count the number of times these conditions become
true during RTL simulation
● Estimate the number of redundant behaviors of each
register from these counts
3. Register grouping algorithm applied and gated clock
introduced for each group
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
8
Register Data Transfer Conditions
 Data Transfer Graph (DTG) captures data transfer condition between
registers (denoted C RT (vi , v j ) )
Example
Courtesy: [Ohnishi97]
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
9
Register Data Transfer Conditions
 Three types of data transfer conditions
CLAT (vi )
Data transfer condition between
register i and one or more source
registers of i
m
C LAT (vi )   CRT (vr , vi )
r 1
CUSED (vi )
Data transfer condition between
register i and one or more destination
registers of i
n
CUSED (vi )   C RT (vi , vr )
r 1
CCHG (vi )
Data transfer condition to one or
more source registers of i
k
CCHG (vi )   C LAT (vr )
r 1
Copyright Agarwal & Srivaths, 2007
Courtesy: [Ohnishi97]
Low-Power Design and Test, Lecture 7
10
Profiling
 Count the number of times CLAT (vi ) , CUSED (vi ), and CCHG (vi )
become true during RTL simulation
■ Call these numbers ALAT (vi ) , AUSED (vi ), and ACHG (vi )
 We can now determine
AHOLD (vi )  ACK (vi )  ALAT (vi )
AUU (vi )  ALAT (vi )  AUSED (vi )
AUC (vi )  ALAT (vi )  ACHG (vi )
 Recall our initial example!
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
11
Register Grouping Algorithm
1.
Record clock cycle in which each register behaves redundantly as follows:
■ Calculate AHOLD  AUU AUC in every cycle for each register
■ If ( AHOLD  AUU  AUC ) cyclet  ( AHOLD  AUU  AUC ) cyclet 1
record t (redundant clocking detected in cycle t)
2.
Greedy grouping of registers
foreach reg i
i,j do not belong to any group
{
Add i to new Group Gi;
foreach reg j
{
#redundancy_similarity= #clock_cycles in which i,j behave redundantly.
if (#redundancy_similarity > threshold)
Add j to Gi;
}
}
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
12
Register Grouping Algorithm
3. Calculate the total redundant power for each group
4. Select groups whose total redundant powers are more than a
given threshold power
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
13
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
14
Pre-computation
 Duplicate part of logic to precompute circuit output values one
cycle before they are required
 Use these values to reduce the
total amount of switching in the
circuit in the next cycle
Original Circuit
(n input, single output)
Circuit with Pre-computation
 Circuit Embodiments
■ g1, g0 : Predictor functions
g1  1  f  1
g0  1  f  0
■ LE = 0; when either g1 or g0
evaluates to 1
Courtesy: [Macii98]
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
15
Pre-computation
 An Example [Devadas95]
■ N-bit comparator
■ Pre-computation circuit based
on the behavior of the
comparison operation
● If the MSBs of C and D are
not equal, C>D can be
evaluated just using the
MSBs
● Otherwise, the rest of the
bits (of C and D) are also
needed.
■ Therefore, LE is given by
LE  C (n  1)  D(n  1)
Copyright Agarwal & Srivaths, 2007
Comparator Circuit
XNOR
Comparator Circuit
with pre-computation
Low-Power Design and Test, Lecture 7
16
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
17
Guarded Evaluation
 Operand Isolation: Use transparent latches as a mechanism for shutting
down redundant switching
■ Latches enabled when useful computation needs to be done
 Guarded Evaluation [Tiwari98]
■ Identifies where transparent latches must be placed
■ Identifies which signals control enable/disable of these latches
Courtesy: [Macii98]
Original Circuit
Copyright Agarwal & Srivaths, 2007
Circuit with Guard
Logic
Low-Power Design and Test, Lecture 7
18
Guarded Evaluation
 An Example RTL Circuit: Dual-operation ALU
■ Ctrl=0 (1) : SHIFT (ADD) operation performed
■ Clock gating will not work here!
REG B
REG A
REG B
REG A
Guard
Logic
SHIFTER
ctrl
ctrl
ADDER
SHIFTER
ctrl
0
ADDER
1
ctrl
0
1
ALU with
Guard Logic
ALU
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
19
Background: Observability Don’t Cares
 Well known concept in logic synthesis
 ODC set of a Boolean variable x: Conditions on the Primary
Inputs such that x is not observable at the Primary Outputs.
 Example: AND gate with inputs x,y and output z
■ x is not observable when y is 0
■ x is not observable when z is not observable
ODC ( x)  y  ODC ( z )
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
20
Guarded Evaluation
 Exploit observability don’t care set
ODCz
■ Set of PI assignments to X so
that the value at z has no
effect at POs.
■ Then the guard logic control
signal s must satisfy the
logical condition
s  ODC z
Circuit with Guard Logic
(Pure Guarded Evaluation)
■ Further,
tl ( s)  te (Y )
Earliest time an input to F can change
Latest settling time of s to 1
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
21
Guarded Evaluation
 Extended Guarded Evaluation
■ Larger set of conditions under
which we can shut off logic
s  ( x  ODC z )
■ Shutdown conditions now include
additionally
● PI assignments not in ODCz
● But, for whom, z=1
Copyright Agarwal & Srivaths, 2007
z
w
s
Low-Power Design and Test, Lecture 7
22
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
23
Behavior-level Power Reduction Techniques
 Recall the equation for dynamic power consumption
Pdyn
1
2
 CVdd * a * f
2
 Two key approaches for reducing power:
■ Use performance speed-up transformations, and trade-off
performance for power through voltage scaling
● How will this work?
■ Reduce the effective capacitance being switched
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
24
Trading off performance for power consumption
benefits
 Exploit voltage and frequency scaling to trade-off performance
gains for significant power consumption savings
 When voltage and frequency
scaling is performed, we can
calculate the power consumption
benefits by determining the new
operating voltage
■ Let Topt be the shortened
execution time due to the use of
performance optimization
■ Assume that the voltage scaled
circuit takes the same time
(TORIG) to complete as the
original circuit
Copyright Agarwal & Srivaths, 2007
Vdd
Topt
TORIG
Vdd
Vddnew
Low-Power Design and Test, Lecture 7
Topt
TORIG
25
Trading off performance for power consumption
benefits
 We have first the following equations for Topt and Torig
Topt  N cyc *1 / f orig
Torig  N cyc *1 / f new
Topt / Torig  f new / f orig
 Dependency of frequency on circuit voltage is given below
f  (Vdd  Vt ) 2 / Vdd
 We therefore have the following equation below for calculating
Vddnew
Topt / Torig  ((Vddnew  Vt ) 2 /(Vdd  Vt ) 2 ) * (Vdd / Vddnew )
Topt / Torig  Vdd new / Vdd
Use Vddnew to calculate final power consumption!
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
26
Performance Optimization Transformations on an
Example Behavior [Chandraskan95]
 Example Behavior of an IIR Filter
YN  X N  A *YN 1
 Behavior Data Flow
XN
YN
+
*
 Design Characteristics
D
A
Copyright Agarwal & Srivaths, 2007
•
•
•
•
•
Vdd = 5V
Critical path Length = 2
Throughput = 2*N
Capacitance = 1 unit
Power = 25 units
Low-Power Design and Test, Lecture 7
27
Transformation (1): Loop Unrolling
 We can unroll the recursive equation once, and get the following
YN 1  X N 1  A *YN 2
YN  X N  A *YN 1
 Behavior Data Flow
XN
 Design Characteristics
YN
+
2D
A
X N 1
* *
+
Copyright Agarwal & Srivaths, 2007
A
•
•
•
•
•
Vdd = 5V
Critical path Length = 2
Throughput = 2*N
Capacitance = 1 unit
Power = 25 units
YN 1
No Low-Power
change
in performance/power!
Design and Test, Lecture 7
28
Transformation (2): Distributivity and Constant
Propagation
 We can apply distributive law and constant propagation
YN 1  X N 1  A *YN 2
YN  X N  A * X N 1  A * YN  2
2
 Behavior Data Flow
XN
+
YN
+
2D
*
A2
A2
X N 1
 Design Characteristics
*
*
+
Copyright Agarwal & Srivaths, 2007
•
•
•
•
•
Vdd = 5V
Critical path Length = 3
Throughput = 3*(N/2)
Capacitance = 1.5 units
Power = 25 units
A
YN 1
Low-Power
• Vdd = 3.75V How?
• Critical path Length = 3
• Throughput = 2*N
• Capacitance = 1.5 units
• Power
= 20
units7
Design
and Test,
Lecture
Voltage
Scaling
29
Transformation (3): Pipelining
 Let us assume we will now process two samples in parallel at any given time
Non-pipelined
operation
……………..
op1
op2
op3
op4
op1
Pipelined
operation
……………..
op2
op3
Copyright Agarwal & Srivaths, 2007
op4
Low-Power Design and Test, Lecture 7
30
Transformation (3): Pipelining
 Behavior Data Flow with Pipelining
■ Observe that the critical path length reduces to 2
XN
+
D
2D
*
A2
A2
X N 1
YN
+
*
D
*
+
A
YN 1
 Design Characteristics
•
•
•
•
•
Vdd = 2.9V How?
Critical path Length = 2
Throughput = 2*N
Capacitance = 1.5 units
Power = 12.5 units (2X reduction)
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
31
Transformation (3): Pipelining
Source: [Chandraskan95]
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
32
Common Case Computation: A PowerOptimization Technique [Lakshminarayana99]
 Recall Amdahl’s law !
 Idea
■ Identify
computations or
sequence of
computations in
behavior that
occur most
frequently
■ Design separate
circuit that
implements
common-case
behavior efficiently
Copyright Agarwal & Srivaths, 2007
Generic Architecture
ORIGINAL
CIRCUIT
Common-case
Detection &
execution
circuit
Activity of energy
optimized circuit
Low-Power Design and Test, Lecture 7
33
CCC: Example [Lakshminarayana99]
GCD Behavior
STG annotated with state and
state transition probabilities
from simulation profiles
while (x != y) {
if (x > y) {
x := x - y;
} else {
y := y - x;
}
}
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
34
CCC: Example [Lakshminarayana99]
Identified
common case behavior
if (x != y) {
if (x > y) {
x := x -y;
}}
if (x != y) {
if (x > y) {
x := x -y;
}}
if (x != y) {
if (x > y) {
x := x -y;
}}
if (x != y) {
if (x > y) {
x := x -y;
}}
Tempx := x - 4y;
if (Tempx > 0) {
x := Tempx;
}
y
x
Common Case
Execution
Copyright Agarwal & Srivaths, 2007
Simplified
common
case behavior
2
Common Case
Detection
0
Low-Power Design and Test, Lecture 7
35
CCC: Results
 Performance improvement of more than 4X!
 Can be traded-off for power savings
■ Average power consumption reduction: 59%
 Average area overhead: 23%
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
36
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Basic Concept
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
37
Operation Reduction: Distributivity
[Chandrakasan95]
 Reducing operations reduces the switched capacitance
2nd order polynomial example
X 2  A* X  B
can be rewritten as
X
X * ( X  A)  B
A
*
+
X
X
+
A
*
+
*
X
B
+
B
X
 One lesser multiplication!
 Same throughput
 No change to the critical path
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
38
Operation Reduction: Distributivity
[Chandrakasan95]
 Reducing operations reduces the switched capacitance
■ Can also increase the critical path (can mean higher voltage
to realize the same throughput)
3rd order polynomial example
X 3  A* X 2  B * X  C
X * ( X * ( X  A)  B)  C
can be rewritten as
A
X
*
X
*
+
+
*
X
A
+
X
+
X
B
+
*
*
B
*
C
#Operations=7
Critical path=4
Copyright Agarwal & Srivaths, 2007
#Operations=5
Critical path=5
Low-Power Design and Test, Lecture 7
X
+
C
39
Strength Reduction and Common Sub-Expression
 Strength Reduction
■ Exploit dissimilarity in energy consumption between operations
■ E.g, Conversion of multiplications with constants into shift-add operations
 Common Sub-Expression
■ Identify common computations between two computational threads and re-use
to reduce the number of operations
 Example: 4-tap FIR Filter [Mehendale95]
Yn  i 0 Ai * X ni
3
X n2
X n1
Xn
Ao
A2
A1
*
X n 3
Coefficients Value
A3
*
*
+
+
Copyright Agarwal & Srivaths, 2007
*
+
Yn
A0
(0.0111011)2
A1
(0.0101011)2
A2
(1.0110011)2
A3
(1.1001010)2
2’s complement
Low-Power Design and Test, Lecture
7
40
fixed-point
arithmetic
Strength Reduction and Common Sub-Expression
 Step 1. Apply Strength Reduction
■ Replace multiplication by equivalent Shift and Add from the binary
representation of the coefficients
Yn  i 0 Ai * X ni  A0 * X 3  A1 * X 2  A2 * X1  A3 * X 0
3
A0 (0.0111011)2
A0 * X 3  2 8 * ( X 3  X 3  1  X 3  3  X 3  4  X 3  5)
A2 (1.0110011)2
A2 * X 1  28 * ( X 1  X 1  1  X 1  4  X 1  5  X 1  7)
#Adds
#Subs
#Shifts
15
2
15
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
41
Strength Reduction and Common Sub-Expression
 Step 2. Identify common sub-expressions across coefficients
■ Two coefficients that have 1 in more than one bit location
A0 * X 3  2 8 * ( X 3  X 3  1  X 3  3  X 3  4  X 3  5)
A2 * X 1  28 * ( X 1  X 1  1  X 1  4  X 1  5  X 1  7)
■ Compute (X1 + X3) = X13 separately
■ Similarly, compute (X0 + X2) = X02 separately
#Adds
#Subs
#Shifts
11
2
10
■ Similarly, Compute (X13 + X13 << 1) = X13_01 separately
#Adds
#Subs
#Shifts
10
2
9
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
42
Outline
 General Observations
 RTL Power Management Techniques
■ Gated Clock Architecture
■ Precomputation
■ Guarded Evaluation
 Behavior-Level Power Reduction Techniques
■ Performance Speedup Techniques
● Algebraic Transformations
● Common Case Computation
■ Switched Capacitance Reduction
● Algebraic Transformations
 Power Supply Gating
■ Power Switches
■ Isolation Cells
■ Retention Flip-Flops
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
43
Power Supply Gating
 Basic Concept:
■ Switches placed on-chip to turn off
power supply when circuit (parts) are
idle.
 Benefits:
■ Leakage power reduction
 Challenges
■ IR drop leads to timing closure issues
■ Simultaneous switching of gating cells
 Two styles of power gating
■ Fine-grained power gating
● Power gating logic part of library
cells
■ Coarse-grained power gating
● Power gating cells part of power
Courtesy [Cadence-PowerMgmtDesignLine06]
grid
network
Low-Power Design and Test, Lecture 7
Copyright Agarwal & Srivaths, 2007
44
Power Supply Gating: An Example [OMAP-ISSCC05]
90nm OMAP2420 SoC
Power Switch used in OMAP
 5 power domains in OMAP SoC enabled by power gating
 Power switches gate VDD, consists of
■ Weak PMOS: Sinks low current for power restore
■ Strong PMOS: Deliver current for normal operation
 2-pass power turn-on mechanism to prevent current surges
■ Weak switches turned on first to almost fully restore VDD(local), and then the strong
switches are turned on to support normal operation
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
45
Power Supply Gating: An Example [OMAPISSCC05]
 Leakage currents
compared between
■ All power domains ON
■ WkUp domain only ON
 Nearly 40X reduction seen
at room temperature
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
46
Isolation Cells
 Special cells used at the interfaces between blocks which are
shut-down and blocks which are on.
 Prevents the outputs of shut-down modules from floating
 Types of Isolation Cells
■ Sets the output to a known value (0 or 1)
■ Sets the output to the last valid value
 Cells and their enables need to be always ON.
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
47
Data Retention
 Things to do before we power down
■ Save state of the module(s) being shut down
 Options [Zyuban02]
■ For processors, OS can save relevant state to local memory
and read back
● Save/restore overheads (time, energy consumption)
■ Use scan to save complete state
■ Keep all latches on a separate power supply and just power
down logic
■ Provide each latch with a shadow latch called retention latch
(each retention latch is on a separate power supply)
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
48
Data Retention
Integrated Scan Retention
Courtesy: [Zyuban-ISLPED02]
Save and Restore Operations
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
49
References

Survey Papers
■ [Devadas95] S. Devadas, S. Malik: A Survey of Optimization Techniques Targeting Low Power VLSI Circuits. DAC 1995:
242-247
■ [Macii98] E. Macii, M. Pedram, F. Somenzi: High-level power modeling, estimation, and optimization. IEEE Trans. on CAD
of Integrated Circuits and Systems 17(11): 1061-1079 (1998)
■
[Chandrakasan95a] A. P. Chandrakasan, M. Potkonjak, R. Mehra, J. Rabaey, and R. Brodersen, ``Optimizing power using
transformations,'' IEEE Trans. Computer-Aided Design, vol. 14, pp. 12--31, Jan. 1995.

RTL Power Management
■ [Ohnishi97] M. Ohnishi, A. Yamada, H. Noda, and T. Kambe, ``A Method of Redundant Clocking Detection and Power
Reduction at the RTL level,'' in Proc. Int. Symp. Low Power Electronics & Design (ISLPED), pp. 131-136, Aug. 1997.
■ [Tiwari98] V. Tiwari, S. Malik, P. Ashar: Guarded evaluation: pushing power management to logic synthesis/design. IEEE
Trans. on CAD of Integrated Circuits and Systems (TCAD) 17(10): 1051-1060 (1998)

Behavioral Power Optimization
■ [Mehendale95] M. Mehendale, S. D. Sherlekar, G. Venkatesh, “Synthesis of multiplier-less FIR filters with minimum number
of additions”. ICCAD 1995: 668-671
■ [Lakshminarayana99] G. Lakshminarayana, A. Raghunathan, K. S. Khouri, N. K. Jha, S. Dey: Common-Case Computation:
A High-Level Technique for Power and Performance Optimization. DAC 1999: 56-61

Power Supply Gating
■ [Cadence-PowerMgmtDesignLine06] Anand Iyer, “Demystify power gating and stop leakage cold”, Power Management
DesignLine, 03/03/06
■ [Zyuban02] V. Zyuban, S. V. Kosonocky: Low power integrated scan-retention mechanism. ISLPED 2002: 98-102
■ [OMAP-ISSCC05] P. Royannez, H. Mair, F. Dahan, M. Wagner et. al.; "90nm Low Leakage SoC Design Techniques for
Wireless Applications"; ISSCC'05, Feb 2005
Copyright Agarwal & Srivaths, 2007
Low-Power Design and Test, Lecture 7
50