Download ee221_3

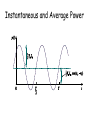
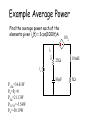
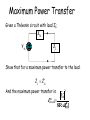
Circuits II
EE221
Unit 3
Instructor: Kevin D. Donohue
Instantaneous, Average, RMS, and
Apparent Power, and, Maximum Power
Transfer, and Power Factors
Power Definitions/Units:



Work is in units of newton-meters or joules
same as energy.
1 joule is work done for 1 ampere passed
through 1 ohm for 1 second, or work done
by a force of 1 Newton applied over 1
meter.
Power is a measure of the rate at which
work is done and is in units ofjoules per
seconds, 746 Watts in one horsepower.
Power Conversion


Electric motors and generators convert
electrical power to mechanical power and
vise versa.
Other devices exist that convert electric
power to light, heat, sound, …. and vise
versa
Instantaneous and Average Power

The instantaneous power is the power absorbed by an
element at an instance of time. In an electric circuit
this is given by:
P(t)v(t)i(t)
where i(t) is the current through the element and v(t) is
the voltage drop over the element.

Average Power over some time interval T is given by:
T
1
P

v
(t)i(t)dt
AV
T0

If the i and v product is periodic, then PAV can be
reduced to the integration over a single period. For
random/non-periodic signals T goes to infinity.
Instantaneous Power


Instantaneous power is simply computed by the
product of 2 functions. For sinusoidal problems,
trig identities or phasors can be used to simplify
the products and result in easier formulae for
average power.
Example: Write a Matlab script that plots the
instantaneous power of a cosine voltage across an
impedance load. Write the script so the voltage
waveform and impedance can be easily changed
and instantaneous power replotted.
Matlab Scripts


A script is a series of Matlab command line
instructions typed in a text file and stored
with an *.m extension. This is referred to
as an mfile.
To run these commands change your
current directory associated with the
Matlab work space to the one containing
the mfile. Then type the base name of the
file in the Matlab command line.
Matlab Scripts


For this example comments are included in
the script, and are identified by text
following a “%” character.
The functions plot and cos are used in this
script. Type help plot or help cos to get a
full description of these functions in the
Matlab workspace.
Matlab Scripts
% This script will plot the instantaneous power absorbed
% by an impedance load with a sinusoidal voltage over it.
% Set the parameters of the Voltage signal
f = 1000; % Frequency of signal in Hz
ph = 30; % Phase of signal in degrees
A=2;
% amplitude of signal
%Set impedance value
zm = 8; % Impedance magnitude
zp = -40; % Impedance phase in degrees
% Create a time axis of 2 periods over which to plot the power
tp = 1/f; % Determine period
t = 2*tp*[0:5000]/5000; % Make a 5001 point time axis (row vector) over 2 periods
Matlab Scripts
% Create a vector of points for voltage
v = A*cos(2*pi*f*t + pi*ph/180);
% Create a vector of points for the current (adjust magnitude and phase
% based on impedance
i = (A/zm)*cos(2*pi*f*t + pi*(ph-zp)/180);
% Take an element by element product to get power
p = v.*i;
% Plot it
plot(t,p)
title(['Instantaneous Power '] )
xlabel(['Seconds'])
ylabel(['Watts'])
Result
Instantaneous Power
0.6
0.5
0.4
Watts
0.3
0.2
0.1
0
-0.1
0
0.2
0.4
0.6
0.8
1
1.2
Seconds
1.4
1.6
1.8
2
-3
x 10
What is the meaning of negative instantaneous power?
Average Power in Periodic Signals
Given a sinusoidal voltage and current in a device:
v
(
t)
A

t

)
vcos(
v
i(
t)
A

t

icos(
i)
Show:
1
P

A


AV A
v
icos(
v
i)
2
Average Power in Periodic Signals
Given a phasor representation of a voltage and
current in a device:
Vˆ  Avv
Iˆ  A
i
i
Show:


1 ˆ
* 1
P

R̂e
V
I
A
A
cos(

)
AV
v
i
v
i
2
2
Instantaneous and Average Power
Conservation of Power
In a given circuit the average power absorb (denoted
by positive values) equals the power delivered
(denoted by negative values).
For a circuit with N elements the sum of all power is
zero:
0
N
P
i
i1
Note: These are all real
or average power values.
Passive Sign Convention
It is assumed that positive charge
entering the positive terminal of
an element implies power
absorbed by the element.
Therefore, charge leaving the
positive terminal of an element
implies power supplied or
delivered by the element.
If the words absorbed or supplied
are not given with a power value,
power absorbed will be assumed.
(A negative sign will imply power
supplied).
I
V
I
V
Example Average Power
Find the average power each of the
elements given is(t) = 3cos(1000t)A
10ia
ia
25Ω
10mH
is
80µF
P25Ω=34.61W
PL=PC=0
P5Ω=21.13W
PCCVS=-5.54W
Pis=-50.19W
5Ω
Maximum Power Transfer
Given a Thévenin circuit with load ZL:
Zth
Vth
ZL
Show that for a maximum power transfer to the load:
Zˆ L  Zˆth*
And the maximum power transfer is:
2
ˆ
V
th
P

max
ˆ*]
8Re[
Z
th
Example Maximum Power
Find the impedance of the load Z to result in the
maximum power transfer, and find the resulting
power. Assume vs(t) = 110cos(377t) V
40µF
8Ω
vs
Z=2.87-75.88
Ith=1.6583.12A
Vth = 4.71 159V
Pz=3.98W
12Ω
7.5mH
Z
Root Mean Square (RMS) Values

The RMS value of a
periodic current or
voltage is its DC
equivalent value for
delivering average
power to a resistor.
2
12
i
(
t
)
2
P

Ri
(
t
)
dt

R
dt

RI
AV
rm
T
T
T
T


Irms

1 2
i (t)dt
T
T

2
2
2
1
v
(
t
) 1
v
(
t
) V
rms
P

dt

dt

AV
T
T
TR R
T R

V

rms

1 2
v(
t)dt
T
T

RMS Formula for Sinusoids
The RMS value for a
sinusoid of any
frequency or phase is
its amplitude divided
by square root of 2.
Irms

1 2 2
Acos
(
t)dt
TT

2
A
j(
t))
exp(
j(
t))
exp(

Irms

dt

T T
2


2

2
A
exp(
dt
Irms

j2(
t))
2exp(
0
)exp(
j2
(
t))
4
TT

2
2
A
A
exp(
dt
Irms

2dt

j2
(
t))
exp(
j2(
t))
4
TT
4
TT

2
A
A
I
 2
T

0

rms
4
T
2

Apparent Power and Power Factor
Apparent power (S) for
sinusoidal waveforms is the
product of the RMS voltage and
current magnitudes without
regard to their phase offsets.
It is in units of Volt-Amps (VA).
The cosine of their phase
difference is the power factor
(pf).
1 1

v
(
t)
A

t

)
vcos(
v
i(
t)
A

t

icos(
i)
Vˆ  Avv
Iˆ  A


i
i


*
ˆ
P

R̂e
V
I
A
A
cos(

)

V
I
cos

)
AV 
v
i
v
i
rms
rms
v
i
2 2
S  Vrms I rms
(apparent power)
PAV  S cos( v   i ) (real power)
Q  S sin( v   i )
(reactive power)
pf  cos( v   i ) (power factor)
Sˆ  Vrms I rms exp  j ( v   i )  (complex power)
Leading and Lagging
The sign of phase difference between the
voltage and current is related to the angle
of the impedance of the load. The terms
leading and lagging are used to describe
this property:




0

pf
leading
(Capac
e
Loa




0

pf
lagging
(Induc
Loa




0

(Only
Real
Load)
v
i
v
i
v
i