* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Power inverter wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Power over Ethernet wikipedia , lookup
Audio power wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Electrification wikipedia , lookup
Power factor wikipedia , lookup
Electrical substation wikipedia , lookup
Electric power system wikipedia , lookup
Stray voltage wikipedia , lookup
Buck converter wikipedia , lookup
History of electric power transmission wikipedia , lookup
Power electronics wikipedia , lookup
Three-phase electric power wikipedia , lookup
Power engineering wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Voltage optimisation wikipedia , lookup
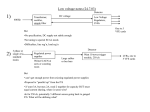
Branch Outage Simulation for Contingency Studies Dr.Aydogan OZDEMIR, Visiting Associate Professor Department of Electrical Engineering, Texas A&M University, College Station TX 77843 Tel : (979) 862 88 97 , Fax : (979) 845 62 59 E-mail : [email protected] Aydoğan Özdemir was born in Artvin, Turkey, on January 1957. He received the B.Sc., M.Sc. and Ph.D. degrees in Electrical Engineering from Istanbul Technical University, Istanbul, Turkey in 1980, 1982 and 1990, respectively. He is an associate professor at the same University. His current research interests are in the area of electric power system with emphasis on reliability analysis, modern tools (neural networks, fuzzy logic, genetic algorithms etc.) for power system modeling, analysis and control and high-voltage engineering. He is a member of National Chamber of Turkish Electrical Engineering and IEEE. Power System Security Power system security is the ability of the system to withstand one or more component outages with the minimal disruption of service or its quality. Outages of component(s) Overstress on the other components No limit violation limit violation(s) operation of protective devices and switching of the unit(s) partial or total loss of load POWER SYSTEM SECURITY monitoring contingency analysis security constrained opf Monitoring : Data collection and state estimation The objective of steady state contingency analysis is to investigate the effects of generation and transmission unit outages on MW line flows and bus voltage magnitudes. START SET SYSTEM MODEL TO INITIAL CONDITIONS SIMULATE AN OUTAGE OF A GENERATOR OR A BRANCH N SELECT A NEW OUTAGE LIMIT VIOLATION Y ALARM MESSAGE N LAST OUTAGE Y END Real-time applications require fast and reliable computation methods due to the high number of possible outages in a moderate power system. However, there is a well-known conflict between the accuracy of the method applied and the calculation speed. Exact solution Full AC power flow for each outage not feasible for real-time applications. Check the limit violations approximate methods to quickly identify conceivable contingencies real-time applications AC power flows only for critical contingencies. Check the limit violations APPROXIMATE CONTINGENCY ANALYSIS Contingency ranking contingencies are ranked in an approximate order of a scalar performance index, PI. contingencies are tested beginning with the most severe one and proceeding down to the less severe ones up to a threshold value. Masking effect causes false orderings and misclassifications. Contingency screening Explicit contingency screening is performed for all contingencies, following an approximate solution (DC load flow, one iteration load flow, linear distribution or sensitivity factors etc.) Contingency screening is performed in the near vicinity of the outages (local solutions) Hybrid methods utilizing both the ranking and the screening outage of a branch or a generation unit MW line flow overloads DC load flows Sensitivity factors voltage magnitude violations both involves more complicated models and better computation algorithms LINE OUTAGE SIMULATION An outage of a line can either be simulated by setting its impedance, yij = 0 or by injecting hypothetical powers at both ends of the line. The latter method is preferred to preserve the original base case bus admittance matrix. i i S ij 0 yi 0 0 yij 0 Sij=0 S ji 0 y j0 0 Z-Matrix techniques Modification of ZBUS is required for each outage Sji=0 j j i S ij 0 S si S ji 0j yij yi 0 y j0 S sj Determination of the hypothetical sources so that all the reactive power circulates through the outaged line while maintaining the same voltage magnitude changes in the system SIMULATION FOR MW LINE FLOW PROBLEM DC LOAD FLOW : ΔP BΔδ , [B']ij 1/ xij , [B']ii 1/ xik , xij Re al{1/ yij } k outage of a line connected between busses i and j ΔP [0 0.. 0 Psi 0... Psi 0..0]T ; Psi Re al{S si } Δδ X[0 0 ..0 1 0 0.. 1..0 0]T Psi , X [B ] 1 The new real power flow through the line connected between busses n and m can be derived and approximated as, 1 ~ Pnm Pnm Pnm Pnm ([X]nn [X]mm - 2[X]nm ) Psi xlm See “Power Generation, Operation and Control by Wood and Wollenberg” for details SIMULATION FOR VOLTAGE MAGNITUDE PROBLEM Linear models are not sufficient for most outages Reactive power flows can not be isolated from bus voltage phase angles Involves more complicated models and better computation algorithms i Qij QijT Q Tji Q Li Qji j Q Lj b Qij Im ag{Vi*. yij .V j } [Vi2 ViV j cos ji ] bij ViV j gij sin ji Vi2 i0 2 Transferring reactive power QijT [Vi2 V j2 ]bij / 2 ViV j gij sin ji QTji QijT assumed to flow through the line Loss reactive power QLi [Vi2 V j2 2ViV j cos ji ] QLj QLi bij b (Vi2 V j2 ) i 0 2 4 assumed to allocated at the busses Can be split up into two parts, Line outage simulation by hypothetical reactive power sources QijT i Q 0 ij Qsi QijT QLi QLi QijT QLi Q ji 0 j Qsi QijT QLi For a tap changing transformer, cross flow through the equivalent impedance is considered to be the transferring reactive power, where shunt flows can be considered as the loss reactive powers. bus i a :1 bus i bij bus j 1 1 ( 1)bij a a QijT QLi bij QTji QLj bus j 1 (1 )bij a Transferring reactive power is sensitive both to bus voltage magnitudes and bus voltage phase angles. However, loss reactive power is dominantly determined by bus voltage phase angles and has a weak coupling with bus voltage magnitudes. Therefore, transferring reactive powers are enough for a reasonable accuracy. Hypothetical reactive power injections to bus i and bus j, will result in a change in net reactive bus powers Qi and Qj. This in turn, will result in a change in system state variables with respect to pre-outage values. This change must be equivalent to the changes when the line is outaged. Load bus reactive powers do not satisfy the nodal power balance equation due to the errors in load bus voltage magnitudes calculated from linear models. Therefore, part of the fictitious reactive generation flows through the neighboring paths instead circulating through the outaged branch. These reactive power mismatches can mathematically be expressed as, * Qi Im ag V Y V i ik k Q ik Q ij Q si Q Di k j k * Q j Im ag V Y V j jk k Q jk Q ji Qsj Q Dj k i k where Qi and QDi are the net reactive power and the reactive demand at load bus i, is the complex voltage at bus i and Yik is the element of bus admittance matrix. The superscript * denotes the conjugate of a complex quantity. Calculated load bus voltage magnitudes need to be modified in a way to minimize the bus reactive power mismatches at both ends of the outaged line. This can be accomplished a local optimization formulation 1. Select an outage of a branch, numbered k and connected between busses i and j. 2. Calculate bus voltage phase angles by using linearized MW flows. l l ( X li X lj ) Pk Pk , l=2,3,…, NB Pij 1 ( X ii X jj 2 X ij ) / x k where X is the inverse of the bus suseptance matrix, Pij is the pre-outage active power flow through the line and xk is the reactance of the line. 3. Calculate intermediate loss reactive powers, ~ ~ Q Li Q Lj 4. Minimize reactive power mismatches at busses i and j, while satisfying linear reactive power flow equations. Mathematically, this corresponds to a constrained optimization process as, Minimize (Qi Qij Q Di ) ( Q j Q ji Q Dj ) T wrt Qij Subject to g q (V ) Q BV ~ Qij QijT QLi ~ Q ji QijT QLi reactive power flows through the outaged line SOLUTION OF THE CONSTRAINED OPTIMIZATION PROBLEM After having formulated the outage simulation as a constrained optimization problem, minimization can be achieved by solution of the partial differential equations of the augmented Lagrangian function L(QijT , V, (Qi Qij QDi ) 2 ( Q j Q ji QDj ) 2 [B 1Q V] with respect to QijT , V and . Note that V does not need to include all the load bus voltage magnitudes; instead only busses i, j and their first order neighbors are enough for optimization cycle. Drawback : Convergence to local maximum Single direction search SOLUTION BY GENETIC ALGORITHMS Evolutionary algorithms are stochastic search methods that mimic the metaphor of natural biological evolution. Genetic Algorithms (GAs) are perhaps the most widely known types of evolutionary computation methods today. GAs operate on a population of potential solutions applying the principle of survival of the fittest procedure better and better approximation to a solution. At each generation, a new set of better approximations is created by selecting individuals according to their fitness in the problem domain. This process leads to the evolution of populations of individuals that are better suited to their environment than the individuals that they were created from. Generate initial population evaluate objective function GENERATE NEW POPULATION selection crossover mutation N optimization criteria met Y best individuals result For the details of the processes see “Cheng, Genetic Algorithms&Engineering Optimization by M. Gen, R., New York: Wiley, 2000 “. Such a single population GA is powerful and performs well on a broad class of optimization problems. BASE CASE LOAD FLOW SELECT AN OUTAGE bounded network CALCULATE BUS VOLTAGE PHASE ANGLES i j outaged branch Minimize Qij Q ji wrt QijT subject to V X Q CALCULATE THE REMAINING QUANTITIES END NUMERICAL EXAMPLES IEEE 14-Bus test System G G 3 2 G 1 5 4 G 8 7 G 6 11 10 9 Base case control variables : PG2 = 0.4 p.u. PG3 = PG6 = PG8 = 0.0 p.u. V1 = 1.06 p.u. V2 = 1.045 p.u. V3 = 1.01 p.u. V6 = 1.07 p.u. V8 = 1.09 p.u. B9 = 0.19 p.u. t4-7 = 0.978 t4-9 = 0.969 t5-6 = 0.932 12 13 14 Q7-9 = 27.24 Mvar Q5-6 = 12.42 MVar Post-Outage Voltage Magnitudes for IEEE-14 Bus Test System Bus Outage of Line 7-9 Outage of transformer 5-6 No VLF [pu] VPF [pu] V [%] VLF [pu] VPF [pu] V [%] 1 1.060 1.060 0.0 1.060 1.060 0.0 2 1.045 1.045 0.0 1.045 1.045 0.0 3 1.010 1.010 0.0 1.010 1.010 0.0 4 1.015 1.015 0.0 1.015 1.023 0.8 5 1.016 1.018 0.2 1.025 1.032 0.7 6 1.070 1.070 0.0 1.070 1.070 0.0 7 1.066 1.068 0.1 1.055 1.055 0.0 8 1.090 1.090 0.0 1.090 1.090 0.0 9 0.988 0.993 0.5 1.046 1.038 0.8 10 0.994 0.999 0.5 1.043 1.036 0.7 11 1.027 1.030 0.3 1.053 1.049 0.4 12 1.050 1.051 0.1 1.052 1.054 0.2 13 1.040 1.041 0.1 1.049 1.048 0.1 14 0.992 0.996 0.4 1.028 1.024 0.4 Maximum error: 0.5 % Maximum error: 0.8 % Post-outage reactive power flows for IEEE-14 Bus Test Systems Line l=m 1-2 Outage of Line 7-9 Outage of transformer 5-6 QPF QDF QPF QDF Q Q [MVa [Mvar [MVar] [Mvar] [Mvar] [Mvar] r] ] -20.3 -20.2 0.07 -21.6 -21.1 0.53 1-5 5.4 4.4 2-3 3.6 3.6 2-4 0.2 -0.1 2-5 2.8 1.7 3-4 5.3 5.0 4-5 12.0 9.0 4-7 -14.1 -14.8 4-9 13.2 12.9 5-6 12.8 13.8 6-11 14.6 12.9 6-12 3.7 3.5 6-13 13.0 12.0 7-9 0.98 0.02 0.27 1.15 0.33 3.02 0.70 0.32 0.97 1.73 0.20 0.96 86.7 9-10 -5.5 -4.8 9-14 -2.6 -1.9 10-11 -11.3 -10.2 12-13 1.9 1.6 13-14 8.3 7.4 7-8 -14.5 -13.3 0.71 0.70 1.11 0.34 0.85 1.21 1.3 3.3 -1.6 -1.3 3.7 8.6 -5.1 3.0 19.5 5.1 15.1 9.6 -8.2 -4.6 -14.9 3.4 12.4 -21.2 -1.3 3.3 -5.8 -4.2 -0.1 14.0 -0.8 6.4 42.6 19.9 4.7 15.5 17.7 -8.9 -5.5 -15.5 3.5 12.2 -21.2 2.64 0.03 4.15 2.90 3.81 5.35 4.31 3.35 0.41 0.36 0.42 8.12 0.66 0.88 0.64 0.06 0.24 0.04 IEEE 57-Bus Test System 5 G 4 3 G G 2 1 16 2 G 45 18 6 19 15 17 14 13 20 21 12 G 46 47 44 48 26 50 24 49 23 38 22 2 39 37 25 40 56 57 41 11 36 27 28 7 29 35 30 33 31 32 34 53 54 52 42 43 55 8 G G 9 10 51 First one is the outage of the line connected between bus-12 and bus-13, whose preoutage reactive power flow is 60.27 Mvar. Second case is the outage of a transformer with turns ratio 0.895 connected between bus-13 and bus-49, whose pre-outage reactive power flows is 33.7 Mvar. Post-Outage Voltage Magnitudes for outage of the line connected between bus 12 and bus V Bus No Voltage magnitudes [p.u.] pre-outage VPF VDF 13 0.979 0.955 0.953 0.0019 14 0.970 0.953 0.951 0.0018 20 0.964 0.955 0.953 0.0016 46 1.060 1.042 1.040 0.0023 47 1.033 1.016 1.014 0.0016 48 1.028 1.011 1.009 0.0020 49 1.036 1.019 1.017 0.0024 threshold error = 0.0015 p.u. Post-Outage Reactive Power Flows for outage of the line connected between bus 12 and bus 13 Reactive Power Flow [MVar] Line pre-outage l-m Qlm Qml 1-2 1-15 3-15 50-51 75.00 -84.12 33.74 -23.95 -18.26 13.73 -4.16 6.51 QPF Qlm QDF Qml Qlm Qml 74.84 -83.94 75.01 84.14 45.29 -34.96 46.26 35.22 0.54 -5.15 0.87 -5.26 -9.43 9.92 -9.23 9.78 threshold error = 0.2 MVar. Q [MVar] 0.17 0.97 0.33 0.20 0.20 0.26 0.11 0.14 Post-Outage Voltage Magnitudes for outage of the transformer connected between bus 13 and bus 49 Bus No 11 13 21 48 49 50 51 Voltage magnitudes [p.u.] pre-outage VPF VDF 0.974 0.976 0.977 0.979 0.985 0.987 1.009 0.982 0.980 1.028 0.997 0.995 1.036 0.978 0.972 1.024 0.980 0.977 1.052 1.038 1.036 threshold error = 0.0015 p.u. V 0.0011 0.0016 0.0017 0.0016 0.0056 0.0032 0.0018 Post-Outage Reactive Power Flows for outage of the transformer connected between bus 12 and bus 13 Reactive Power Flow [MVar] Line l-m 3-15 12-13 15-45 14-46 47-48 48-49 50-51 10-51 pre-outage Qlm Qml -18.26 13.73 60.27 -64.01 -0.79 2.15 27.32 -25.39 12.36 -12.26 -7.40 6.95 -6.16 6.51 12.47 -11.81 QPF QDF Qlm Qml Qlm Qml -15.59 11.01 -17.09 12.53 52.49 -56.76 50.06 -54.46 7.67 -5.67 9.33 -7.36 42.82 -39.29 45.93 -42.24 24.76 -24.41 22.71 -22.27 5.93 -6.10 4.31 -4.20 -13.25 14.53 -11.84 13.35 21.06 -19.83 23.24 -21.98 threshold error = 1.0 MVar. Q [MVar] 1.50 2.43 1.66 3.11 2.05 1.62 1.41 2.18 1.52 2.30 1.69 2.95 2.14 1.90 1.18 2.15