* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch9-12
Mathematics of radio engineering wikipedia , lookup
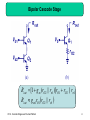
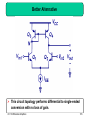
Negative resistance wikipedia , lookup
Standing wave ratio wikipedia , lookup
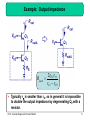
Electronic engineering wikipedia , lookup
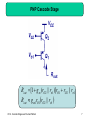
Audio crossover wikipedia , lookup
Power electronics wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
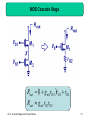
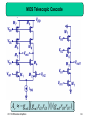
Switched-mode power supply wikipedia , lookup
Schmitt trigger wikipedia , lookup
Index of electronics articles wikipedia , lookup
Equalization (audio) wikipedia , lookup
RLC circuit wikipedia , lookup
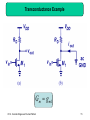
Wilson current mirror wikipedia , lookup
Public address system wikipedia , lookup
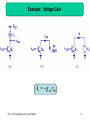
Phase-locked loop wikipedia , lookup
Current mirror wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Radio transmitter design wikipedia , lookup
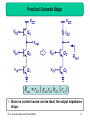
Regenerative circuit wikipedia , lookup
Positive feedback wikipedia , lookup
Instrument amplifier wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
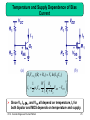
Rectiverter wikipedia , lookup
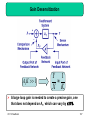
Operational amplifier wikipedia , lookup
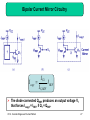
Opto-isolator wikipedia , lookup
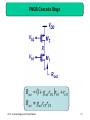
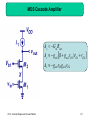
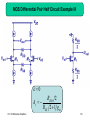
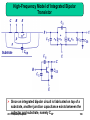
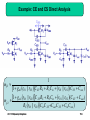
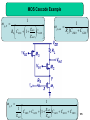
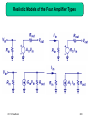
Fundamentals of Microelectronics II CH9 CH10 CH11 CH12 Cascode Stages and Current Mirrors Differential Amplifiers Frequency Response Feedback 1 Chapter 9 Cascode Stages and Current Mirrors 9.1 Cascode Stage 9.2 Current Mirrors 2 Boosted Output Impedances Rout1 1 g m RE || r rO RE || r Rout 2 1 g m RS rO RS CH 9 Cascode Stages and Current Mirrors 3 Bipolar Cascode Stage Rout [1 g m (rO 2 || r 1 )]rO1 rO 2 || r 1 Rout g m1rO1 rO 2 || r 1 CH 9 Cascode Stages and Current Mirrors 4 Maximum Bipolar Cascode Output Impedance Rout , max g m1rO1r 1 Rout , max 1rO1 The maximum output impedance of a bipolar cascode is bounded by the ever-present r between emitter and ground of Q1. CH 9 Cascode Stages and Current Mirrors 5 Example: Output Impedance RoutA 2rO 2 r 1 r 1 rO 2 Typically r is smaller than rO, so in general it is impossible to double the output impedance by degenerating Q2 with a resistor. CH 9 Cascode Stages and Current Mirrors 6 PNP Cascode Stage Rout [1 g m (rO 2 || r 1 )]rO1 rO 2 || r 1 Rout g m1rO1 rO 2 || r 1 CH 9 Cascode Stages and Current Mirrors 7 Another Interpretation of Bipolar Cascode Instead of treating cascode as Q2 degenerating Q1, we can also think of it as Q1 stacking on top of Q2 (current source) to boost Q2’s output impedance. CH 9 Cascode Stages and Current Mirrors 8 False Cascodes Rout 1 1 1 g m1 || rO 2 || r 1 rO1 || rO 2 || r 1 g m2 g m2 Rout g m1 1 rO1 1 2rO1 g m2 g m2 When the emitter of Q1 is connected to the emitter of Q2, it’s no longer a cascode since Q2 becomes a diode-connected device instead of a current source. CH 9 Cascode Stages and Current Mirrors 9 MOS Cascode Stage Rout 1 g m1rO 2 rO1 rO 2 Rout g m1rO1rO 2 CH 9 Cascode Stages and Current Mirrors 10 Another Interpretation of MOS Cascode Similar to its bipolar counterpart, MOS cascode can be thought of as stacking a transistor on top of a current source. Unlike bipolar cascode, the output impedance is not limited by . CH 9 Cascode Stages and Current Mirrors 11 PMOS Cascode Stage Rout 1 g m1rO 2 rO1 rO 2 Rout g m1rO1rO 2 CH 9 Cascode Stages and Current Mirrors 12 Example: Parasitic Resistance Rout (1 g m1rO 2 )(rO1 || RP ) rO 2 RP will lower the output impedance, since its parallel combination with rO1 will always be lower than rO1. CH 9 Cascode Stages and Current Mirrors 13 Short-Circuit Transconductance iout Gm vin vout 0 The short-circuit transconductance of a circuit measures its strength in converting input voltage to output current. CH 9 Cascode Stages and Current Mirrors 14 Transconductance Example Gm g m1 CH 9 Cascode Stages and Current Mirrors 15 Derivation of Voltage Gain vout iout Rout Gm vin Rout vout vin Gm Rout By representing a linear circuit with its Norton equivalent, the relationship between Vout and Vin can be expressed by the product of Gm and Rout. CH 9 Cascode Stages and Current Mirrors 16 Example: Voltage Gain Av g m1rO1 CH 9 Cascode Stages and Current Mirrors 17 Comparison between Bipolar Cascode and CE Stage Since the output impedance of bipolar cascode is higher than that of the CE stage, we would expect its voltage gain to be higher as well. CH 9 Cascode Stages and Current Mirrors 18 Voltage Gain of Bipolar Cascode Amplifier Gm g m1 Av g m1rO1 g m1 (rO1 || r 2 ) Since rO is much larger than 1/gm, most of IC,Q1 flows into the diode-connected Q2. Using Rout as before, AV is easily calculated. CH 9 Cascode Stages and Current Mirrors 19 Alternate View of Cascode Amplifier A bipolar cascode amplifier is also a CE stage in series with a CB stage. CH 9 Cascode Stages and Current Mirrors 20 Practical Cascode Stage Rout rO3 || g m2 rO 2 (rO1 || r 2 ) Since no current source can be ideal, the output impedance drops. CH 9 Cascode Stages and Current Mirrors 21 Improved Cascode Stage Rout g m3 rO3 (rO 4 || r 3 ) || g m2 rO 2 (rO1 || r 2 ) In order to preserve the high output impedance, a cascode PNP current source is used. CH 9 Cascode Stages and Current Mirrors 22 MOS Cascode Amplifier Av Gm Rout Av g m1 (1 g m 2 rO 2 )rO1 rO 2 Av g m1rO1 g m 2 rO 2 CH 9 Cascode Stages and Current Mirrors 23 Improved MOS Cascode Amplifier Ron g m 2 rO 2 rO1 Rop g m3 rO 3 rO 4 Rout Ron || Rop Similar to its bipolar counterpart, the output impedance of a MOS cascode amplifier can be improved by using a PMOS cascode current source. CH 9 Cascode Stages and Current Mirrors 24 Temperature and Supply Dependence of Bias Current R2V CC ( R1 R2 ) VT ln(I1 I S ) 1 W R2 I1 n Cox VDD VTH 2 L R1 R2 2 Since VT, IS, n, and VTH all depend on temperature, I1 for both bipolar and MOS depends on temperature and supply. CH 9 Cascode Stages and Current Mirrors 25 Concept of Current Mirror The motivation behind a current mirror is to sense the current from a “golden current source” and duplicate this “golden current” to other locations. CH 9 Cascode Stages and Current Mirrors 26 Bipolar Current Mirror Circuitry I copy I S1 I S , REF I REF The diode-connected QREF produces an output voltage V1 that forces Icopy1 = IREF, if Q1 = QREF. CH 9 Cascode Stages and Current Mirrors 27 Bad Current Mirror Example I Without shorting the collector and base of QREF together, there will not be a path for the base currents to flow, therefore, Icopy is zero. CH 9 Cascode Stages and Current Mirrors 28 Bad Current Mirror Example II Although a path for base currents exists, this technique of biasing is no better than resistive divider. CH 9 Cascode Stages and Current Mirrors 29 Multiple Copies of IREF I copy , j IS, j I S , REF I REF Multiple copies of IREF can be generated at different locations by simply applying the idea of current mirror to more transistors. CH 9 Cascode Stages and Current Mirrors 30 Current Scaling I copy , j nI REF By scaling the emitter area of Qj n times with respect to QREF, Icopy,j is also n times larger than IREF. This is equivalent to placing n unit-size transistors in parallel. CH 9 Cascode Stages and Current Mirrors 31 Example: Scaled Current CH 9 Cascode Stages and Current Mirrors 32 Fractional Scaling I copy 1 I REF 3 A fraction of IREF can be created on Q1 by scaling up the emitter area of QREF. CH 9 Cascode Stages and Current Mirrors 33 Example: Different Mirroring Ratio Using the idea of current scaling and fractional scaling, Icopy2 is 0.5mA and Icopy1 is 0.05mA respectively. All coming from a source of 0.2mA. CH 9 Cascode Stages and Current Mirrors 34 Mirroring Error Due to Base Currents I copy nI REF 1 1 n 1 CH 9 Cascode Stages and Current Mirrors 35 Improved Mirroring Accuracy I copy nI REF 1 1 2 n 1 Because of QF, the base currents of QREF and Q1 are mostly supplied by QF rather than IREF. Mirroring error is reduced times. CH 9 Cascode Stages and Current Mirrors 36 Example: Different Mirroring Ratio Accuracy I copy1 I REF 15 4 2 I copy 2 10I REF 15 4 2 CH 9 Cascode Stages and Current Mirrors 37 PNP Current Mirror PNP current mirror is used as a current source load to an NPN amplifier stage. CH 9 Cascode Stages and Current Mirrors 38 Generation of IREF for PNP Current Mirror CH 9 Cascode Stages and Current Mirrors 39 Example: Current Mirror with Discrete Devices Let QREF and Q1 be discrete NPN devices. IREF and Icopy1 can vary in large magnitude due to IS mismatch. CH 9 Cascode Stages and Current Mirrors 40 MOS Current Mirror The same concept of current mirror can be applied to MOS transistors as well. CH 9 Cascode Stages and Current Mirrors 41 Bad MOS Current Mirror Example This is not a current mirror since the relationship between VX and IREF is not clearly defined. The only way to clearly define VX with IREF is to use a diodeconnected MOS since it provides square-law I-V relationship. CH 9 Cascode Stages and Current Mirrors 42 Example: Current Scaling Similar to their bipolar counterpart, MOS current mirrors can also scale IREF up or down (I1 = 0.2mA, I2 = 0.5mA). CH 9 Cascode Stages and Current Mirrors 43 CMOS Current Mirror The idea of combining NMOS and PMOS to produce CMOS current mirror is shown above. CH 9 Cascode Stages and Current Mirrors 44 Chapter 10 Differential Amplifiers 10.1 General Considerations 10.2 Bipolar Differential Pair 10.3 MOS Differential Pair 10.4 Cascode Differential Amplifiers 10.5 Common-Mode Rejection 10.6 Differential Pair with Active Load 45 Audio Amplifier Example An audio amplifier is constructed above that takes on a rectified AC voltage as its supply and amplifies an audio signal from a microphone. CH 10 Differential Amplifiers 46 “Humming” Noise in Audio Amplifier Example However, VCC contains a ripple from rectification that leaks to the output and is perceived as a “humming” noise by the user. CH 10 Differential Amplifiers 47 Supply Ripple Rejection v X Av vin vr vY vr v X vY Av vin Since both node X and Y contain the ripple, their difference will be free of ripple. CH 10 Differential Amplifiers 48 Ripple-Free Differential Output Since the signal is taken as a difference between two nodes, an amplifier that senses differential signals is needed. CH 10 Differential Amplifiers 49 Common Inputs to Differential Amplifier v X Av vin vr vY Av vin vr v X vY 0 Signals cannot be applied in phase to the inputs of a differential amplifier, since the outputs will also be in phase, producing zero differential output. CH 10 Differential Amplifiers 50 Differential Inputs to Differential Amplifier v X Av vin vr vY Av vin vr v X vY 2 Av vin When the inputs are applied differentially, the outputs are 180° out of phase; enhancing each other when sensed differentially. CH 10 Differential Amplifiers 51 Differential Signals A pair of differential signals can be generated, among other ways, by a transformer. Differential signals have the property that they share the same average value to ground and are equal in magnitude but opposite in phase. CH 10 Differential Amplifiers 52 Single-ended vs. Differential Signals CH 10 Differential Amplifiers 53 Differential Pair With the addition of a tail current, the circuits above operate as an elegant, yet robust differential pair. CH 10 Differential Amplifiers 54 Common-Mode Response VBE 1 VBE 2 I C1 I C 2 I EE 2 V X VY VCC CH 10 Differential Amplifiers I EE RC 2 55 Common-Mode Rejection Due to the fixed tail current source, the input commonmode value can vary without changing the output commonmode value. CH 10 Differential Amplifiers 56 Differential Response I I C1 I EE IC2 0 V X VCC RC I EE VY VCC CH 10 Differential Amplifiers 57 Differential Response II I C 2 I EE I C1 0 VY VCC RC I EE V X VCC CH 10 Differential Amplifiers 58 Differential Pair Characteristics None-zero differential input produces variations in output currents and voltages, whereas common-mode input produces no variations. CH 10 Differential Amplifiers 59 Small-Signal Analysis I EE I C1 I 2 I EE IC2 I 2 Since the input to Q1 and Q2 rises and falls by the same amount, and their bases are tied together, the rise in IC1 has the same magnitude as the fall in IC2. CH 10 Differential Amplifiers 60 Virtual Ground VP 0 I C1 g m V I C 2 g m V For small changes at inputs, the gm’s are the same, and the respective increase and decrease of IC1 and IC2 are the same, node P must stay constant to accommodate these changes. Therefore, node P can be viewed as AC ground. CH 10 Differential Amplifiers 61 Small-Signal Differential Gain 2 g m VRC Av g m RC 2V Since the output changes by -2gmVRC and input by 2V, the small signal gain is –gmRC, similar to that of the CE stage. However, to obtain same gain as the CE stage, power dissipation is doubled. CH 10 Differential Amplifiers 62 Large Signal Analysis I C1 IC2 CH 10 Differential Amplifiers Vin1 Vin 2 I EE exp VT Vin1 Vin 2 1 exp VT I EE Vin1 Vin 2 1 exp VT 63 Input/Output Characteristics Vout1 Vout 2 Vin1 Vin 2 RC I EE tanh 2VT CH 10 Differential Amplifiers 64 Linear/Nonlinear Regions The left column operates in linear region, whereas the right column operates in nonlinear region. CH 10 Differential Amplifiers 65 Small-Signal Model CH 10 Differential Amplifiers 66 Half Circuits vout1 vout 2 g m RC vin1 vin 2 Since VP is grounded, we can treat the differential pair as two CE “half circuits”, with its gain equal to one half circuit’s single-ended gain. CH 10 Differential Amplifiers 67 Example: Differential Gain vout1 vout 2 g m rO vin1 vin 2 CH 10 Differential Amplifiers 68 Extension of Virtual Ground VX 0 It can be shown that if R1 = R2, and points A and B go up and down by the same amount respectively, VX does not move. CH 10 Differential Amplifiers 69 Half Circuit Example I Av g m1 rO1 || rO3 || R1 CH 10 Differential Amplifiers 70 Half Circuit Example II Av g m1 rO1 || rO3 || R1 CH 10 Differential Amplifiers 71 Half Circuit Example III Av CH 10 Differential Amplifiers RC 1 RE gm 72 Half Circuit Example IV Av CH 10 Differential Amplifiers RC RE 1 2 gm 73 MOS Differential Pair’s Common-Mode Response V X VY VDD I SS RD 2 Similar to its bipolar counterpart, MOS differential pair produces zero differential output as VCM changes. CH 10 Differential Amplifiers 74 Equilibrium Overdrive Voltage VGS VTH equil I SS W n Cox L The equilibrium overdrive voltage is defined as the overdrive voltage seen by M1 and M2 when both of them carry a current of ISS/2. CH 10 Differential Amplifiers 75 Minimum Common-mode Output Voltage VDD I SS RD VCM VTH 2 In order to maintain M1 and M2 in saturation, the commonmode output voltage cannot fall below the value above. This value usually limits voltage gain. CH 10 Differential Amplifiers 76 Differential Response CH 10 Differential Amplifiers 77 Small-Signal Response VP 0 Av g m RD Similar to its bipolar counterpart, the MOS differential pair exhibits the same virtual ground node and small signal gain. CH 10 Differential Amplifiers 78 Power and Gain Tradeoff In order to obtain the source gain as a CS stage, a MOS differential pair must dissipate twice the amount of current. This power and gain tradeoff is also echoed in its bipolar counterpart. CH 10 Differential Amplifiers 79 MOS Differential Pair’s Large-Signal Response I D1 I D 2 4 I SS 1 W 2 n Cox Vin1 V in 2 Vin1 Vin 2 W 2 L n Cox L CH 10 Differential Amplifiers 80 Maximum Differential Input Voltage Vin1 Vin 2 max 2 VGS VTH equil There exists a finite differential input voltage that completely steers the tail current from one transistor to the other. This value is known as the maximum differential input voltage. CH 10 Differential Amplifiers 81 Contrast Between MOS and Bipolar Differential Pairs MOS Bipolar In a MOS differential pair, there exists a finite differential input voltage to completely switch the current from one transistor to the other, whereas, in a bipolar pair that voltage is infinite. CH 10 Differential Amplifiers 82 The effects of Doubling the Tail Current Since ISS is doubled and W/L is unchanged, the equilibrium overdrive voltage for each transistor must increase by 2 to accommodate this change, thus Vin,max increases by 2 as well. Moreover, since ISS is doubled, the differential output swing will double. CH 10 Differential Amplifiers 83 The effects of Doubling W/L Since W/L is doubled and the tail current remains unchanged, the equilibrium overdrive voltage will be lowered by 2 to accommodate this change, thus Vin,max will be lowered by 2 as well. Moreover, the differential output swing will remain unchanged since neither ISS nor RD has changed CH 10 Differential Amplifiers 84 Small-Signal Analysis of MOS Differential Pair I D1 I D 2 4 I SS 1 W W n Cox Vin1 Vin 2 n Cox I SS Vin1 Vin 2 W 2 L L n Cox L When the input differential signal is small compared to 4ISS/nCox(W/L), the output differential current is linearly proportional to it, and small-signal model can be applied. CH 10 Differential Amplifiers 85 Virtual Ground and Half Circuit VP 0 Av g m RC Applying the same analysis as the bipolar case, we will arrive at the same conclusion that node P will not move for small input signals and the concept of half circuit can be used to calculate the gain. CH 10 Differential Amplifiers 86 MOS Differential Pair Half Circuit Example I 0 1 Av g m1 || rO 3 || rO1 g m3 CH 10 Differential Amplifiers 87 MOS Differential Pair Half Circuit Example II 0 g m1 Av g m3 CH 10 Differential Amplifiers 88 MOS Differential Pair Half Circuit Example III 0 RDD 2 Av RSS 2 1 g m CH 10 Differential Amplifiers 89 Bipolar Cascode Differential Pair Av g m1 g m3 rO1 || r 3 rO3 rO1 CH 10 Differential Amplifiers 90 Bipolar Telescopic Cascode Av g m1 g m3 rO3 rO1 || r 3 || g m5 rO5 (rO7 || r 5 ) CH 10 Differential Amplifiers 91 Example: Bipolar Telescopic Parasitic Resistance R1 R1 Rop rO 5 1 g m 5 rO 7 || r 5 || rO 7 || r 5 || 2 2 Av g m1 g m 3 rO 3 (rO1 || r 3 ) || Rop CH 10 Differential Amplifiers 92 MOS Cascode Differential Pair Av g m1rO3 g m3 rO1 CH 10 Differential Amplifiers 93 MOS Telescopic Cascode Av g m1 g m3 rO3 rO1 || ( g m5 rO5 rO7 ) CH 10 Differential Amplifiers 94 Example: MOS Telescopic Parasitic Resistance Rop rO 5 || [ R1 1 g m5 rO 7 rO 7 ] Av g m1 ( Rop || rO 3 g m3 rO1 ) CH 10 Differential Amplifiers 95 Effect of Finite Tail Impedance Vout ,CM Vin ,CM RC / 2 REE 1 / 2 g m If the tail current source is not ideal, then when a input CM voltage is applied, the currents in Q1 and Q2 and hence output CM voltage will change. CH 10 Differential Amplifiers 96 Input CM Noise with Ideal Tail Current CH 10 Differential Amplifiers 97 Input CM Noise with Non-ideal Tail Current CH 10 Differential Amplifiers 98 Comparison As it can be seen, the differential output voltages for both cases are the same. So for small input CM noise, the differential pair is not affected. CH 10 Differential Amplifiers 99 CM to DM Conversion, ACM-DM Vout RD VCM 1 / g m 2 REE If finite tail impedance and asymmetry are both present, then the differential output signal will contain a portion of input common-mode signal. CH 10 Differential Amplifiers 100 Example: ACM-DM ACM DM R C 1 2[1 g m3 ( R1 || r 3 )]rO 3 R1 || r 3 g m1 CH 10 Differential Amplifiers 101 CMRR CMRR ADM ACM DM CMRR defines the ratio of wanted amplified differential input signal to unwanted converted input common-mode noise that appears at the output. CH 10 Differential Amplifiers 102 Differential to Single-ended Conversion Many circuits require a differential to single-ended conversion, however, the above topology is not very good. CH 10 Differential Amplifiers 103 Supply Noise Corruption The most critical drawback of this topology is supply noise corruption, since no common-mode cancellation mechanism exists. Also, we lose half of the signal. CH 10 Differential Amplifiers 104 Better Alternative This circuit topology performs differential to single-ended conversion with no loss of gain. CH 10 Differential Amplifiers 105 Active Load With current mirror used as the load, the signal current produced by the Q1 can be replicated onto Q4. This type of load is different from the conventional “static load” and is known as an “active load”. CH 10 Differential Amplifiers 106 Differential Pair with Active Load The input differential pair decreases the current drawn from RL by I and the active load pushes an extra I into RL by current mirror action; these effects enhance each other. CH 10 Differential Amplifiers 107 Active Load vs. Static Load The load on the left responds to the input signal and enhances the single-ended output, whereas the load on the right does not. CH 10 Differential Amplifiers 108 MOS Differential Pair with Active Load Similar to its bipolar counterpart, MOS differential pair can also use active load to enhance its single-ended output. CH 10 Differential Amplifiers 109 Asymmetric Differential Pair Because of the vastly different resistance magnitude at the drains of M1 and M2, the voltage swings at these two nodes are different and therefore node P cannot be viewed as a virtual ground. CH 10 Differential Amplifiers 110 Thevenin Equivalent of the Input Pair vThev g mN roN (vin1 vin 2 ) RThev 2roN CH 10 Differential Amplifiers 111 Simplified Differential Pair with Active Load vout g mN (rON || rOP ) vin1 vin 2 CH 10 Differential Amplifiers 112 Proof of VA << Vout vout vA 2 g mP rOP A I vout I g m4v A rO 4 CH 10 Differential Amplifiers 113 Chapter 11 Frequency Response 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 Fundamental Concepts High-Frequency Models of Transistors Analysis Procedure Frequency Response of CE and CS Stages Frequency Response of CB and CG Stages Frequency Response of Followers Frequency Response of Cascode Stage Frequency Response of Differential Pairs Additional Examples CH 10 Differential Amplifiers 114 Chapter Outline CH 11 10 Frequency Differential Response Amplifiers 115 High Frequency Roll-off of Amplifier As frequency of operation increases, the gain of amplifier decreases. This chapter analyzes this problem. CH 11 10 Frequency Differential Response Amplifiers 116 Example: Human Voice I Natural Voice Telephone System Natural human voice spans a frequency range from 20Hz to 20KHz, however conventional telephone system passes frequencies from 400Hz to 3.5KHz. Therefore phone conversation CH 11 10 Frequency Differential Response Amplifiers differs from face-to-face conversation. 117 Example: Human Voice II Path traveled by the human voice to the voice recorder Mouth Air Recorder Path traveled by the human voice to the human ear Mouth Air Ear Skull Since the paths are different, the results will also be different. CH 11 10 Frequency Differential Response Amplifiers 118 Example: Video Signal High Bandwidth Low Bandwidth Video signals without sufficient bandwidth become fuzzy as they fail to abruptly change the contrast of pictures from complete white into complete black. CH 11 10 Frequency Differential Response Amplifiers 119 Gain Roll-off: Simple Low-pass Filter In this simple example, as frequency increases the impedance of C1 decreases and the voltage divider consists of C1 and R1 attenuates Vin to a greater extent at the output. CH 11 10 Frequency Differential Response Amplifiers 120 Gain Roll-off: Common Source Vout 1 g mVin RD || C s L The capacitive load, CL, is the culprit for gain roll-off since at high frequency, it will “steal” away some signal current and shunt it to ground. CH 11 10 Frequency Differential Response Amplifiers 121 Frequency Response of the CS Stage Vout Vin g m RD RD2 C L2 2 1 At low frequency, the capacitor is effectively open and the gain is flat. As frequency increases, the capacitor tends to a short and the gain starts to decrease. A special frequency isFrequency ω=1/(R CH 11 10 Differential Response Amplifiers 122 DCL), where the gain drops by 3dB. Example: Figure of Merit F .O.M . 1 VT VCC C L This metric quantifies a circuit’s gain, bandwidth, and power dissipation. In the bipolar case, low temperature, supply, and load capacitance mark a superior figure of merit. CH 11 10 Frequency Differential Response Amplifiers 123 Example: Relationship between Frequency Response and Step Response H s j 1 R12C12 2 1 t Vout t V0 1 exp u t R1C1 The relationship is such that as R1C1 increases, the bandwidth drops and the step response becomes slower. CH 11 10 Frequency Differential Response Amplifiers 124 Bode Plot s s 1 1 z1 z 2 H ( s ) A0 s s 1 1 p1 p2 When we hit a zero, ωzj, the Bode magnitude rises with a slope of +20dB/dec. When we hit a pole, ωpj, the Bode magnitude falls with a slope ofResponse -20dB/dec CH 11 10 Frequency Differential Amplifiers 125 Example: Bode Plot p1 1 RD C L The circuit only has one pole (no zero) at 1/(RDCL), so the slope drops from 0 to -20dB/dec as we pass ωp1. CH 11 10 Frequency Differential Response Amplifiers 126 Pole Identification Example I p1 p2 1 RS Cin Vout Vin CH 11 10 Frequency Differential Response Amplifiers 1 1 RD C L g m RD 2 p21 1 2 p2 2 127 Pole Identification Example II p1 1 1 RS || Cin gm CH 11 10 Frequency Differential Response Amplifiers p2 1 RD C L 128 Circuit with Floating Capacitor The pole of a circuit is computed by finding the effective resistance and capacitance from a node to GROUND. The circuit above creates a problem since neither terminal ofFrequency CF isResponse grounded. CH 11 10 Differential Amplifiers 129 Miller’s Theorem ZF Z1 1 Av ZF Z2 1 1 / Av If Av is the gain from node 1 to 2, then a floating impedance ZF can be converted to two grounded impedances Z1 and Z2. CH 11 10 Frequency Differential Response Amplifiers 130 Miller Multiplication With Miller’s theorem, we can separate the floating capacitor. However, the input capacitor is larger than the original floating capacitor. We call this Miller multiplication. CH 11 10 Frequency Differential Response Amplifiers 131 Example: Miller Theorem 1 in RS 1 g m RD C F CH 11 10 Frequency Differential Response Amplifiers out 1 1 C F RD 1 g m RD 132 High-Pass Filter Response Vout Vin R1C1 R12C1212 1 The voltage division between a resistor and a capacitor can be configured such that the gain at low frequency is reduced. CH 11 10 Frequency Differential Response Amplifiers 133 Example: Audio Amplifier Ci 79.6nF CL 39.8nF Ri 100K g m 1 / 200 In order to successfully pass audio band frequencies (20 Hz-20 KHz), large input and output capacitances are needed. CH 11 10 Frequency Differential Response Amplifiers 134 Capacitive Coupling vs. Direct Coupling Capacitive Coupling Direct Coupling Capacitive coupling, also known as AC coupling, passes AC signals from Y to X while blocking DC contents. This technique allows independent bias conditions between stages. Direct coupling does not. CH 11 10 Frequency Differential Response Amplifiers 135 Typical Frequency Response Lower Corner CH 11 10 Frequency Differential Response Amplifiers Upper Corner 136 High-Frequency Bipolar Model C Cb C je At high frequency, capacitive effects come into play. Cb represents the base charge, whereas C and Cje are the junction capacitances. CH 11 10 Frequency Differential Response Amplifiers 137 High-Frequency Model of Integrated Bipolar Transistor Since an integrated bipolar circuit is fabricated on top of a substrate, another junction capacitance exists between the collector and substrate, namely CCS. CH 11 10 Frequency Differential Response Amplifiers 138 Example: Capacitance Identification CH 11 10 Frequency Differential Response Amplifiers 139 MOS Intrinsic Capacitances For a MOS, there exist oxide capacitance from gate to channel, junction capacitances from source/drain to substrate, and overlap capacitance from gate to CH 11 10 Frequency Differential Response Amplifiers source/drain. 140 Gate Oxide Capacitance Partition and Full Model The gate oxide capacitance is often partitioned between source and drain. In saturation, C2 ~ Cgate, and C1 ~ 0. They are in parallel with the overlap capacitance to form CGS and CGD. CH 11 10 Frequency Differential Response Amplifiers 141 Example: Capacitance Identification CH 11 10 Frequency Differential Response Amplifiers 142 Transit Frequency gm 2f T CGS gm 2f T C Transit frequency, fT, is defined as the frequency where the current gain from input to output drops to 1. CH 11 10 Frequency Differential Response Amplifiers 143 Example: Transit Frequency Calculation 2fT 3 n VGS VTH 2 2L L 65nm VGS VTH 100mV n 400cm 2 /(V .s ) fT 226GHz CH 11 10 Frequency Differential Response Amplifiers 144 Analysis Summary The frequency response refers to the magnitude of the transfer function. Bode’s approximation simplifies the plotting of the frequency response if poles and zeros are known. In general, it is possible to associate a pole with each node in the signal path. Miller’s theorem helps to decompose floating capacitors into grounded elements. Bipolar and MOS devices exhibit various capacitances that limit the speed of circuits. CH 11 10 Frequency Differential Response Amplifiers 145 High Frequency Circuit Analysis Procedure Determine which capacitor impact the low-frequency region of the response and calculate the low-frequency pole (neglect transistor capacitance). Calculate the midband gain by replacing the capacitors with short circuits (neglect transistor capacitance). Include transistor capacitances. Merge capacitors connected to AC grounds and omit those that play no role in the circuit. Determine the high-frequency poles and zeros. Plot the frequency response using Bode’s rules or exact analysis. CH 11 10 Frequency Differential Response Amplifiers 146 Frequency Response of CS Stage with Bypassed Degeneration Vout g m RD RS Cb s 1 s VX RS Cb s g m RS 1 In order to increase the midband gain, a capacitor Cb is placed in parallel with Rs. The pole frequency must be well below the lowest signal frequency to avoid the effect of degeneration. CH 11 10 Frequency Differential Response Amplifiers 147 Unified Model for CE and CS Stages CH 11 10 Frequency Differential Response Amplifiers 148 Unified Model Using Miller’s Theorem CH 11 10 Frequency Differential Response Amplifiers 149 Example: CE Stage RS 200 I C 1mA 100 C 100 fF C 20 fF CCS 30 fF p ,in 2 516MHz p ,out 2 1.59GHz The input pole is the bottleneck for speed. CH 11 10 Frequency Differential Response Amplifiers 150 Example: Half Width CS Stage W 2X p ,in p ,out CH 11 10 Frequency Differential Response Amplifiers 1 C g R C RS in 1 m L XY 2 2 2 1 Cout 2 C XY RL 1 2 g R 2 m L 151 Direct Analysis of CE and CS Stages gm | z | C XY | p1 | 1 RThev Cin RL C XY Cout 1 g m RL C XY RThev 1 g m RL C XY RThev RThev Cin RL C XY Cout | p 2 | RThev RL Cin C XY Cout C XY Cin Cout Direct analysis yields different pole locations and an extra zero. CH 11 10 Frequency Differential Response Amplifiers 152 Example: CE and CS Direct Analysis p1 1 1 g m1 rO1 || rO 2 C XY RS RS Cin rO1 || rO 2 (C XY Cout ) 1 g m1 rO1 || rO 2 C XY RS RS Cin rO1 || rO 2 (C XY Cout ) p2 RS rO1 || rO 2 Cin C XY Cout C XY Cin Cout CH 11 10 Frequency Differential Response Amplifiers 153 Example: Comparison Between Different Methods RS 200 CGS 250 fF CGD 80 fF CDB 100 fF g m 150 1 0 RL 2 K Dominant Pole Miller’s Exact p ,in 2 571MHz p ,in 2 264MHz p ,in 2 249MHz p ,out 2 428MHz p ,out 2 4.53GHz p ,out 2 4.79GHz CH 10 Differential Amplifiers CH 11 Frequency Response 154 154 Input Impedance of CE and CS Stages 1 1 Z in || r Z in CGS 1 g m RD CGD s C 1 g m RC C s CH 11 10 Frequency Differential Response Amplifiers 155 Low Frequency Response of CB and CG Stages Vout g m RC Ci s s 1 g m RS Ci s g m Vin As with CE and CS stages, the use of capacitive coupling leads to low-frequency roll-off in CB and CG stages (although a CB stage is shown above, a CG stage is similar). CH 11 10 Frequency Differential Response Amplifiers 156 Frequency Response of CB Stage p, X 1 1 RS || C X gm C X C p ,Y rO CH 11 10 Frequency Differential Response Amplifiers 1 RL CY CY C CCS 157 Frequency Response of CG Stage 1 p , Xr O 1 RS || C X gm C X CGS CSB p ,Y rO 1 RL CY CY CGD CDB Similar to a CB stage, the input pole is on the order of fT, so rarely a speed bottleneck. CH 11 10 Frequency Differential Response Amplifiers 158 Example: CG Stage Pole Identification p, X 1 1 RS || C SB1 CGD1 g m1 CH 11 10 Frequency Differential Response Amplifiers p ,Y 1 1 C DB1 CGD1 CGS 2 C DB 2 g m2 159 Example: Frequency Response of CG Stage RS 200 CGS 250 fF CGD 80 fF C DB 100 fF g m 150 p , X 2 5.31GHz 0 p ,Y 2 442MHz 1 Rd 2 K CH 10 Differential Amplifiers CH 11 Frequency Response 160 160 Emitter and Source Followers The following will discuss the frequency response of emitter and source followers using direct analysis. Emitter follower is treated first and source follower is derived easily by allowing r to go to infinity. CH 11 10 Frequency Differential Response Amplifiers 161 Direct Analysis of Emitter Follower Vout Vin C 1 s gm 2 as bs 1 CH 11 10 Frequency Differential Response Amplifiers RS C C C C L C C L a gm C RS b RS C 1 gm r CL gm 162 Direct Analysis of Source Follower Stage Vout Vin CGS 1 s gm 2 as bs 1 CH 11 10 Frequency Differential Response Amplifiers RS CGD CGS CGDC SB CGS C SB a gm CGD C SB b RS CGD gm 163 Example: Frequency Response of Source Follower RS 200 C L 100 fF CGS 250 fF CGD 80 fF C DB 100 fF g m 150 1 0 CH Differential Response Amplifiers CH 10 11 Frequency p1 2 1.79GHz j 2.57GHz p 2 2 1.79GHz j 2.57GHz 164 164 Example: Source Follower Vout Vin CGS 1 s gm 2 as bs 1 RS CGD1CGS1 (CGD1 CGS1 )(C SB1 CGD 2 C DB 2 ) a g m1 CGD1 C SB1 C GD 2 C DB 2 b RS CGD1 g m1 CH 11 10 Frequency Differential Response Amplifiers 165 Input Capacitance of Emitter/Source Follower rO C / CGS Cin C / CGD 1 g m RL CH 11 10 Frequency Differential Response Amplifiers 166 Example: Source Follower Input Capacitance 1 Cin CGD1 CGS1 1 g m1 rO1 || rO 2 CH 11 10 Frequency Differential Response Amplifiers 167 Output Impedance of Emitter Follower V X RS r C s r RS IX r C s 1 CH 11 10 Frequency Differential Response Amplifiers 168 Output Impedance of Source Follower V X RS CGS s 1 I X CGS s g m CH 11 10 Frequency Differential Response Amplifiers 169 Active Inductor The plot above shows the output impedance of emitter and source followers. Since a follower’s primary duty is to lower the driving impedance (RS>1/gm), the “active inductor” characteristic on the right is usually observed. CH 11 10 Frequency Differential Response Amplifiers 170 Example: Output Impedance rO V X rO1 || rO 2 CGS 3 s 1 IX CGS 3 s g m3 CH 11 10 Frequency Differential Response Amplifiers 171 Frequency Response of Cascode Stage Av , XY g m1 1 g m2 C x 2C XY For cascode stages, there are three poles and Miller multiplication is smaller than in the CE/CS stage. CH 11 10 Frequency Differential Response Amplifiers 172 Poles of Bipolar Cascode p, X 1 RS || r 1 C 1 2C 1 p ,out CH 11 10 Frequency Differential Response Amplifiers p ,Y 1 1 CCS1 C 2 2C1 g m2 1 RL CCS 2 C 2 173 Poles of MOS Cascode p, X 1 g m1 CGD1 RS CGS1 1 g m2 p ,Y CH 11 10 Frequency Differential Response Amplifiers p ,out 1 RL C DB 2 CGD 2 1 1 g m2 g m2 C DB1 CGS 2 1 g m1 CGD1 174 Example: Frequency Response of Cascode RS 200 CGS 250 fF CGD 80 fF C DB 100 fF g m 150 1 p , X 2 1.95GHz 0 p ,Y 2 1.73GHz RL 2 K p ,out 2 442MHz CH Differential Response Amplifiers CH 10 11 Frequency 175 175 MOS Cascode Example p, X 1 g m1 CGD1 RS CGS1 1 g m2 p ,Y 1 C DB1 CGS 2 CH 11 10 Frequency Differential Response Amplifiers g m2 1 g m2 1 g m1 p ,out 1 RL C DB 2 CGD 2 CGD1 CGD3 C DB 3 176 I/O Impedance of Bipolar Cascode 1 Z in r 1 || C 1 2C1 s CH 11 10 Frequency Differential Response Amplifiers Z out 1 RL || C 2 CCS 2 s 177 I/O Impedance of MOS Cascode 1 Z in g m1 CGS1 1 g CGD1 s m2 CH 11 10 Frequency Differential Response Amplifiers Z out 1 RL || CGD2 C DB 2 s 178 Bipolar Differential Pair Frequency Response Half Circuit Since bipolar differential pair can be analyzed using halfcircuit, its transfer function, I/O impedances, locations of poles/zeros are the same as that of the half circuit’s. CH 11 10 Frequency Differential Response Amplifiers 179 MOS Differential Pair Frequency Response Half Circuit Since MOS differential pair can be analyzed using halfcircuit, its transfer function, I/O impedances, locations of poles/zeros are the same as that of the half circuit’s. CH 11 10 Frequency Differential Response Amplifiers 180 Example: MOS Differential Pair p, X p ,Y p ,out CH 11 10 Frequency Differential Response Amplifiers 1 RS [CGS1 (1 g m1 / g m 3 )CGD1 ] 1 g m3 CGD1 C DB1 CGS 3 1 g m1 1 RL C DB 3 CGD3 1 g m3 181 Common Mode Frequency Response Vout g R R C 1 m D SS SS VCM RSS CSS s 2 g m RSS 1 Css will lower the total impedance between point P to ground at high frequency, leading to higher CM gain which degrades the CM rejection ratio. CH 10 Differential Amplifiers CH 11 Frequency Response 182 182 Tail Node Capacitance Contribution Source-Body Capacitance of M1, M2 and M3 Gate-Drain Capacitance of M3 CH 11 10 Frequency Differential Response Amplifiers 183 Example: Capacitive Coupling Rin2 RB 2 || r 2 1RE L1 1 2 542 Hz r 1 || RB1 C1 CH 10 Differential Amplifiers CH 11 Frequency Response L 2 1 22.9 Hz RC Rin2 C2 184 184 Example: IC Amplifier – Low Frequency Design Rin2 CH 11 10 Frequency Differential Response Amplifiers RF 1 Av 2 L1 g m1 RS1 1 2 42.4MHz RS 1C1 L 2 1 2 6.92MHz RD1 Rin2 C2 185 Example: IC Amplifier – Midband Design vX g m1 RD1 || Rin2 3.77 vin CH 10 Differential Amplifiers CH 11 Frequency Response 186 186 Example: IC Amplifier – High Frequency Design p1 2 (308 MHz ) p 2 2 (2.15 GHz ) p3 1 RL 2 (1.15CGD 2 C DB 2 ) 2 (1.21 GHz ) CH 10 Differential Amplifiers CH 11 Frequency Response 187 187 Chapter 12 Feedback 12.1 General Considerations 12.2 Types of Amplifiers 12.3 Sense and Return Techniques 12.4 Polarity of Feedback 12.5 Feedback Topologies 12.6 Effect of Finite I/O Impedances 12.7 Stability in Feedback Systems 188 Negative Feedback System A negative feedback system consists of four components: 1) feedforward system, 2) sense mechanism, 3) feedback network, and 4) comparison mechanism. CH 12 Feedback 189 Close-loop Transfer Function A1 Y X 1 KA1 CH 12 Feedback 190 Feedback Example Y X A1 R2 1 A1 R1 R2 A1 is the feedforward network, R1 and R2 provide the sensing and feedback capabilities, and comparison is provided by differential input of A1. CH 12 Feedback 191 Comparison Error E X E 1 A1 K As A1K increases, the error between the input and fed back signal decreases. Or the fed back signal approaches a good replica of the input. CH 12 Feedback 192 Comparison Error R1 Y 1 X R2 CH 12 Feedback 193 Loop Gain X 0 VN KA1 Vtest When the input is grounded, and the loop is broken at an arbitrary location, the loop gain is measured to be KA1. CH 12 Feedback 194 Example: Alternative Loop Gain Measurement VN KA1Vtest CH 12 Feedback 195 Incorrect Calculation of Loop Gain Signal naturally flows from the input to the output of a feedforward/feedback system. If we apply the input the other way around, the “output” signal we get is not a result of the loop gain, but due to poor isolation. CH 12 Feedback 196 Gain Desensitization A1 K 1 Y 1 X K A large loop gain is needed to create a precise gain, one that does not depend on A1, which can vary by ±20%. CH 12 Feedback 197 Ratio of Resistors When two resistors are composed of the same unit resistor, their ratio is very accurate. Since when they vary, they will vary together and maintain a constant ratio. CH 12 Feedback 198 Merits of Negative Feedback 1) Bandwidth enhancement 2) Modification of I/O Impedances 3) Linearization CH 12 Feedback 199 Bandwidth Enhancement Closed Loop Open Loop As Negative Feedback A0 1 s 0 A0 1 KA0 Y s s X 1 1 KA0 0 Although negative feedback lowers the gain by (1+KA0), it also extends the bandwidth by the same amount. CH 12 Feedback 200 Bandwidth Extension Example As the loop gain increases, we can see the decrease of the overall gain and the extension of the bandwidth. CH 12 Feedback 201 Example: Open Loop Parameters A0 g m RD 1 Rin gm CH 12 Feedback Rout RD 202 Example: Closed Loop Voltage Gain vout vin CH 12 Feedback g m RD R2 1 g m RD R1 R2 203 Example: Closed Loop I/O Impedance R2 1 1 Rin g m RD g m R1 R2 CH 12 Feedback Rout RD R2 1 g m RD R1 R2 204 Example: Load Desensitization W/O Feedback Large Difference g m RD g m RD / 3 CH 12 Feedback With Feedback Small Difference g m RD g m RD R2 R2 1 g m RD 3 g m RD R1 R2 R1 R2 205 Linearization Before feedback After feedback CH 12 Feedback 206 Four Types of Amplifiers CH 12 Feedback 207 Ideal Models of the Four Amplifier Types CH 12 Feedback 208 Realistic Models of the Four Amplifier Types CH 12 Feedback 209 Examples of the Four Amplifier Types CH 12 Feedback 210 Sensing a Voltage In order to sense a voltage across two terminals, a voltmeter with ideally infinite impedance is used. CH 12 Feedback 211 Sensing and Returning a Voltage Feedback Network R1 R2 Similarly, for a feedback network to correctly sense the output voltage, its input impedance needs to be large. R1 and R2 also provide a mean to return the voltage. CH 12 Feedback 212 Sensing a Current A current is measured by inserting a current meter with ideally zero impedance in series with the conduction path. The current meter is composed of a small resistance r in parallel with a voltmeter. CH 12 Feedback 213 Sensing and Returning a Current Feedback Network RS 0 Similarly for a feedback network to correctly sense the current, its input impedance has to be small. RS has to be small so that its voltage drop will not change Iout. CH 12 Feedback 214 Addition of Two Voltage Sources Feedback Network In order to add or substrate two voltage sources, we place them in series. So the feedback network is placed in series with the input source. CH 12 Feedback 215 Practical Circuits to Subtract Two Voltage Sources Although not directly in series, Vin and VF are being subtracted since the resultant currents, differential and single-ended, are proportional to the difference of Vin and VF. CH 12 Feedback 216 Addition of Two Current Sources Feedback Network In order to add two current sources, we place them in parallel. So the feedback network is placed in parallel with the input signal. CH 12 Feedback 217 Practical Circuits to Subtract Two Current Sources Since M1 and RF are in parallel with the input current source, their respective currents are being subtracted. Note, RF has to be large enough to approximate a current source. CH 12 Feedback 218 Example: Sense and Return R1 and R2 sense and return the output voltage to feedforward network consisting of M1- M4. M1 and M2 also act as a voltage subtractor. CH 12 Feedback 219 Example: Feedback Factor CH 12 Feedback iF K g mF vout 220 Input Impedance of an Ideal Feedback Network To sense a voltage, the input impedance of an ideal feedback network must be infinite. To sense a current, the input impedance of an ideal feedback network must be zero. CH 12 Feedback 221 Output Impedance of an Ideal Feedback Network To return a voltage, the output impedance of an ideal feedback network must be zero. To return a current, the output impedance of an ideal feedback network must be infinite. CH 12 Feedback 222 Determining the Polarity of Feedback 1) Assume the input goes either up or down. 2) Follow the signal through the loop. 3) Determine whether the returned quantity enhances or opposes the original change. CH 12 Feedback 223 Polarity of Feedback Example I Vin CH 12 Feedback I D1 , I D 2 Vout ,Vx Negative Feedback I D 2 , I D1 224 Polarity of Feedback Example II Vin CH 12 Feedback I D1 ,V A Vout ,Vx Negative Feedback I D1 ,V A 225 Polarity of Feedback Example III I in CH 12 Feedback I D1 ,VX Vout , I D 2 Positive Feedback I D1 ,VX 226 Voltage-Voltage Feedback Vout A0 Vin 1 KA0 CH 12 Feedback 227 Example: Voltage-Voltage Feedback Vout Vin CH 12 Feedback g mN ( rON || rOP ) R2 1 g mN ( rON || rOP ) R1 R2 228 Input Impedance of a V-V Feedback Vin Rin (1 A0 K ) I in A better voltage sensor CH 12 Feedback 229 Example: V-V Feedback Input Impedance Vin R2 1 1 g m RD I in g m R1 R2 CH 12 Feedback 230 Output Impedance of a V-V Feedback Rout VX I X 1 KA0 A better voltage source CH 12 Feedback 231 Example: V-V Feedback Output Impedance Rout , closed CH 12 Feedback R1 1 1 R2 g mN 232 Voltage-Current Feedback CH 12 Feedback V out RO I in 1 KRO 233 Example: Voltage-Current Feedback Vout g m 2 RD1 RD 2 g m 2 RD1 RD 2 I in 1 RF CH 12 Feedback 234 Input Impedance of a V-C Feedback Rin VX IX 1 R0 K A better current sensor. CH 12 Feedback 235 Example: V-C Feedback Input Impedance Rin , closed CH 12 Feedback 1 . g m1 1 g m 2 RD1 RD 2 1 RF 236 Output Impedance of a V-C Feedback Rout VX IX 1 R0 K A better voltage source. CH 12 Feedback 237 Example: V-C Feedback Output Impedance Rout , closed CH 12 Feedback RD 2 g m 2 RD1 RD 2 1 RF 238 Current-Voltage Feedback I out Gm Vin 1 KG m CH 12 Feedback 239 Example: Current-Voltage Feedback Laser I out g m1 g m3 rO 3 || rO 5 |closed Vin 1 g m1 g m3 rO 3 || rO 5 RM CH 12 Feedback 240 Input Impedance of a C-V Feedback V in Rin (1 KG m ) I in A better voltage sensor. CH 12 Feedback 241 Output Impedance of a C-V Feedback VX Rout (1 KG m ) IX A better current source. CH 12 Feedback 242 Example: Current-Voltage Feedback I out g m1 g m 2 RD |closed Vin 1 g m1 g m 2 RD RM Laser 1 Rin |closed (1 g m1 g m 2 RD RM ) g m1 Rout CH 12 Feedback 1 |closed (1 g m1 g m 2 RD RM ) g m2 243 Wrong Technique for Measuring Output Impedance If we want to measure the output impedance of a C-V closed-loop feedback topology directly, we have to place VX in series with K and Rout. Otherwise, the feedback will be disturbed. CH 12 Feedback 244 Current-Current Feedback CH 12 Feedback I out AI I in 1 KAI 245 Input Impedance of C-C Feedback Rin VX I X 1 KAI A better current sensor. CH 12 Feedback 246 Output Impedance of C-C Feedback VX Rout (1 KAI ) IX A better current source. CH 12 Feedback 247 Example: Test of Negative Feedback Laser I in CH 12 Feedback VD1 , I out VP , I F Negative Feedback VD1 , I out 248 Example: C-C Negative Feedback Laser g m 2 RD AI |closed 1 g m 2 R D ( RM / R F ) 1 1 Rin |closed . g m1 1 g m 2 RD ( RM / RF ) Rout |closed rO 2 [1 g m 2 RD ( R M / RF )] CH 12 Feedback 249 How to Break a Loop The correct way of breaking a loop is such that the loop does not know it has been broken. Therefore, we need to present the feedback network to both the input and the output of the feedforward amplifier. CH 12 Feedback 250 Rules for Breaking the Loop of Amplifier Types CH 12 Feedback 251 Intuitive Understanding of these Rules Voltage-Voltage Feedback Since ideally, the input of the feedback network sees zero impedance (Zout of an ideal voltage source), the return replicate needs to be grounded. Similarly, the output of the feedback network sees an infinite impedance (Zin of an ideal voltage sensor), the sense replicate needs to be open. Similar ideas apply to the other types. CH 12 Feedback 252 Rules for Calculating Feedback Factor CH 12 Feedback 253 Intuitive Understanding of these Rules Voltage-Voltage Feedback Since the feedback senses voltage, the input of the feedback is a voltage source. Moreover, since the return quantity is also voltage, the output of the feedback is left open (a short means the output is always zero). Similar ideas apply to the other types. CH 12 Feedback 254 Breaking the Loop Example I Av , open g m1 RD || R1 R2 Rin , open 1 / g m1 CH 12 Feedback Rout , open RD || R1 R2 255 Feedback Factor Example I K R2 /( R1 R2 ) Av , closed Av , open /(1 KAv , open ) Rin , closed Rin , open (1 KAv , open ) Rout , closed Rout , closed /(1 KAv , open ) CH 12 Feedback 256 Breaking the Loop Example II Av ,open g mN rON || rOP || R1 R2 Rin ,open Rout ,open rON || rOP || R1 R2 CH 12 Feedback 257 Feedback Factor Example II K R2 /( R1 R2 ) Av , closed Av , open /(1 KAv , open ) Rin , closed CH 12 Feedback Rout , closed Rout , open /(1 KAv , open ) 258 Breaking the Loop Example IV Vout RF RD1 |open . g m 2 RD 2 || RF 1 I in RF g m1 Rin , open CH 12 Feedback 1 || RF g m1 Rout , open RD 2 || RF 259 Feedback Factor Example IV K 1 / RF Vout Vout Vout |closed |open /(1 K |open ) I in I in I in Rin , closed Rin , open Vout /(1 K |open ) I in Rout , closed Rout , open CH 12 Feedback Vout /(1 K |open ) I in 260 Breaking the Loop Example V I out g m3 rO 3 || rO 5 g m1rO1 |open Vin rO1 RL RM Rin ,open Rout ,open rO1 RM CH 12 Feedback 261 Feedback Factor Example V K RM ( I out / Vin |closed ) ( I out / Vin |open ) /[1 K ( I out / Vin ) |open ] Rin , closed Rout , closed Rout , open [1 K ( I out / Vin ) |open ] CH 12 Feedback 262 Breaking the Loop Example VI I out g m1 RD |open Vin R L RM 1 / g m 2 Rin ,open 1 / g m1 CH 12 Feedback Rout ,open (1 / g m 2 ) RM 263 Feedback Factor Example VI K RM ( I out / Vin |closed ) ( I out / Vin |open ) /[1 K ( I out / Vin ) |open ] Rin , closed Rin , open [1 K ( I out / Vin ) |open ] Rout , closed Rout , open [1 K ( I out / Vin ) |open ] CH 12 Feedback 264 Breaking the Loop Example VII AI , open Rin , open g m 2 rO 2 ( R F RM ) R D . 1 rO 2 RL RM || RF R F RM g m1 1 || ( RF RM ) g m1 Rout , open rO 2 RF || RM CH 12 Feedback 265 Feedback Factor Example VII K RM /( RF RM ) AI ,closed AI ,open /(1 KAI ,open ) Rin ,closed Rin ,open /(1 KAI ,open ) CH 12 Feedback Rout ,closed Rout ,open (1 KAI ,open ) 266 Breaking the Loop Example VIII Vout RF RD |open [ g m 2 ( RF || RM )] I in RF 1 / g m1 Rin , open 1 || RF g m1 Rout , open RF || RM CH 12 Feedback 267 Feedback Factor Example VIII K 1 / RF (Vout / I in ) |closed (Vout / I in ) |open /[1 K (Vout / I in ) |open ] Rin ,closed Rin ,open /[1 K (Vout / I in ) |open ] Rout ,closed Rout ,open /[1 K (Vout / I in ) |open ] CH 12 Feedback 268 Example: Phase Response As it can be seen, the phase of H(jω) starts to drop at 1/10 of the pole, hits -45o at the pole, and approaches -90o at 10 times the pole. CH 12 Feedback 269 Example: Three-Pole System For a three-pole system, a finite frequency produces a phase of -180o, which means an input signal that operates at this frequency will have its output inverted. CH 12 Feedback 270 Instability of a Negative Feedback Loop Y H ( s) (s) X 1 KH ( s ) Substitute jω for s. If for a certain ω1, KH(jω1) reaches -1, the closed loop gain becomes infinite. This implies for a very small input signal at ω1, the output can be very large. Thus the system becomes unstable. CH 12 Feedback 271 “Barkhausen’s Criteria” for Oscillation | KH ( j1 ) | 1 KH ( j1 ) 180 CH 12 Feedback 272 Time Evolution of Instability CH 12 Feedback 273 Oscillation Example This system oscillates, since there’s a finite frequency at which the phase is -180o and the gain is greater than unity. In fact, this system exceeds the minimum oscillation requirement. CH 12 Feedback 274 Condition for Oscillation Although for both systems above, the frequencies at which |KH|=1 and KH=-180o are different, the system on the left is still unstable because at KH=-180o, |KH|>1. Whereas the system on the right is stable because at KH=-180o, |KH|<1. CH 12 Feedback 275 Condition for Stability GX PX ωPX, (“phase crossover”), is the frequency at which KH=-180o. ωGX, (“gain crossover”), is the frequency at which |KH|=1. CH 12 Feedback 276 Stability Example I | H p | 1 K 1 CH 12 Feedback 277 Stability Example II 0.5 | H p | 1 K 0.5 CH 12 Feedback 278 Marginally Stable vs. Stable Marginally Stable CH 12 Feedback Stable 279 Phase Margin Phase Margin = H(ωGX)+180 The larger the phase margin, the more stable the negative feedback becomes CH 12 Feedback 280 Phase Margin Example PM 45 CH 12 Feedback 281 Frequency Compensation Phase margin can be improved by moving ωGX closer to origin while maintaining ωPX unchanged. CH 12 Feedback 282 Frequency Compensation Example Ccomp is added to lower the dominant pole so that ωGX occurs at a lower frequency than before, which means phase margin increases. CH 12 Feedback 283 Frequency Compensation Procedure 1) We identify a PM, then -180o+PM gives us the new ωGX, or ωPM. 2) On the magnitude plot at ωPM, we extrapolate up with a slope of +20dB/dec until we hit the low frequency gain then we look “down” and the frequency we see is our new dominant pole, ωP’. CH 12 Feedback 284 Example: 45o Phase Margin Compensation PM p 2 CH 12 Feedback 285 Miller Compensation Ceq [1 g m5 (rO 5 || rO 6 )]Cc To save chip area, Miller multiplication of a smaller capacitance creates an equivalent effect. CH 12 Feedback 286