* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Nonlinear Dynamics of Soil Moisture and Mineral Nitrogen
Survey
Document related concepts
Transcript
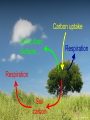
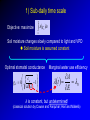
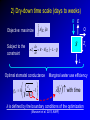
Eco-hydrological optimality to link water use and carbon gains by plants Manzoni S.1,2, G. Vico2, S. Palmroth3, G. Katul3,4, and A. Porporato3,4 1Physical 2Crop Production Ecology and Ecology Dept., SLU, Uppsala 3Nicholas 4Civil Geography and Quaternary Geology, Stockholm Univ. School of the Environment, Duke Univ., USA and Environmental Engineering, Duke Univ., USA PHOTO BY S. MANZONI Carbon uptake Food, fiber, biofuels… Respiration Respiration Soil carbon PHOTO BY S. MANZONI Stomatal conductance as a “compromise between the need to provide a passage for assimilation and the prevention of excessive transpiration” (Cowan and Troughton, 1971, Planta) Carbon uptake Transpiration A E Rainfall Soil moisture PHOTO BY S. MANZONI How do plants respond to altered climatic conditions? Can we optimize agroecosystem management to balance productivity and resource use? Can we breed crops towards more efficient resource use? Regulation of water transport Stomatal closure limits evaporation from the leaves gc LAI gc(P) -ψP gP E -ψP Manzoni et al. (2013) Adv. Water Res. Lens (2011), New Phytologist Plant xylem limits transport of liquid water to the leaves Water use strategies involve tradeoffs 1) High transpiration allows plants to grow faster → competitive advantage (Eagleson, 2002, Rodriguez-Iturbe and Porporato 2004) BUT: high transpiration lowers soil moisture faster → earlier water stress? 2) Stomatal closure reduces desiccation risk (Cowan, 1982) BUT: lower stomatal conductance decreases C uptake → carbon starvation? Tradeoffs require ‘balanced’ solutions Hypothesis: Water use strategies are optimal in a given environment (idea pioneered by Givnish, Cowan and Farquhar) 1) Objective: maximize photosynthesis (A) 2) Control: stomatal conductance to CO2 (gC) 3) Constraint: soil water is limited Process-based optimal control problem Optimality at different time scales Water use strategies vary with the temporal scale of interest, because environmental drivers fluctuate at different scales Data from Fazenda Tamandua, Brazil 1) Sub-daily, at ~constant soil moisture 2) One dry-down (days-weeks) R 3) Several years and longer: stochastic soil moisture Stomatal controls on transpiration and photosynthesis Stomatal cavity From the xylem C fixation wi ci Guard cells gc E wa A ca The water flux is driven by the atmospheric evaporative demand E agC wi wa agC D The CO2 flux is driven by the gradient between atmospheric and internal CO2 concentrations A gC ca ci k Qci Biochemical C fixation Stomatal controls on transpiration and photosynthesis Downward concavity! The water flux is driven by the atmospheric evaporative demand E agC wi wa agC D A(gc) E(gc) gc g C kca A g C k gC The CO2 flux is driven by the gradient between atmospheric and internal CO2 concentrations A gC ca ci k Qci Biochemical C fixation 1) Sub-daily time scale T Objective: maximize Ag dt c 0 Soil moisture changes slowly compared to light and VPD Soil moisture is assumed constant Optimal stomatal conductance ca g C k 1 aD Marginal water use efficiency A t 0 E λ is constant, but undetermined! (classical solution by Cowan and Farquhar; Hari and Mäkelä) λ = constant at given soil moisture Palmroth et al., 1999, Oecologia Correct scaling gc and E vs. vapor pressure deficit D Katul et al., 2009, PCE Proportionality of gc and A (see also Hari et al., 2000, Aus. J. Plant Phys.) 2) Dry-down time scale (days to weeks) R E T Objective: maximize Ag dt Q c 0 Subject to the constraint ds nZ r R E g c L Q dt s Zr L Optimal stomatal conductance Marginal water use efficiency ca g C k 1 aD t with time λ is defined by the boundary conditions of the optimization (Manzoni et al. 2013, AWR) (Manzoni et al., 2011, Functional Ecol) λ increases with decreasing water availability -ψ gc -ψ λ/λww λww Water use efficiency λ ww e a aΨ Water stress λ increases as drought progresses across species, ecosystems, and climates 3) Optimal water use in stochastic environments SPAC model gc LAI gc Ψ90,s Transpiration – moisture curve depends on plant hydraulic traits gP ψ50 E -ψP -ψP s → p(s) depends on the ds R E L Q E(s) curve and hence also Constraint: nZ r dt on plant hydraulic traits Stochastic rainfall 3) Optimal water use in stochastic environments → p(s) depends on the ds R E L Q E(s) curve and hence also Constraint: nZ r dt on plant hydraulic traits → Plant strategies optimize the long-term mean C uptake Objective: maximize A As ps ds 0 → Focus on stomatal and xylem conductances: What is the optimal shape of gc(P) and gP(P)? ψ50 <A> gP Optimal water use explains plant trait coordination A -ψP Observations are consistent with prediction of coordinated stomatal closure and cavitation occurrence Ψ90,s gc LAI gc -ψP Conclusions 1. Sub-daily time scale: optimization explains stomatal responses to air humidity and photosynthesis-transpiration relations 2. Dry-down time scale: plants optimally down-regulate water losses as soils dry 3. Long term: coordination among plant hydraulic traits emerges as an optimal evolutionary strategy