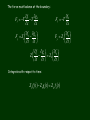Download Reflection and Transmission

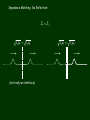
Reflection and Transmission
What force must be applied at end of a string to launch a pulse?
F
THERE ARE TWO FORCES TO CONSIDER !!!!!!
Force on a string segment Dx:
(from when we derived the wave equation)
As Dx goes to zero, Fy and mass go to zero, but acceleration of the string
segment remains finite.
It had better – we need a force to move the string to get a wave equation !
T
Vertical force at the string end:
Fy  T sin  
(Tension force at end)
The Impedance Creed
The string end is an interface.
It has no width. It has no mass.
There is no limit to apply.
It cannot have a net force applied to it.
A net force would be equivalent to an infinite stress.
A net force at the end would rip the string.
The driver must therefore balance this force.
If
y = f(x-vt):
Force needed is proportional to
the transverse velocity, like a
damping force!
Constant of proportionality is the
characteristic impedance:
Z  T
The change in impedance at an interface determines the
amounts of reflection and transmission.
Z1  T1
f1  x  vt 
g1  x  vt 
Z 2  T 2
f 2  x  vt 
The string must be continuous at the boundary:
f1 t   g1 t   f 2 t 
The force must balance at the boundary:
f1
g1
Fy  T
T
x
x
f 2
Fy  T
x
f g
Fy  Z1  1  1 
 t t 
f
Fy  Z 2  2 
 t 
f1 g1 
f 2 


Z1  
  Z2  
 t t 
 t 
Integrate with respect to time:
Z1 f1 t   Z1 g1 t   Z 2 f 2 t 
Z1 f1 t   Z1 g1 t   Z 2 f1 t   Z 2 g1 t 
Z1 g1 t   Z 2 g1 t   Z1 f1 t   Z 2 f1 t 
r
g1 t  Z1  Z 2

f1 t  Z1  Z 2
reflection
coefficient
Z1 f1 t   Z1 f 2 t   Z1 f1 t   Z 2 f 2 t 
 Z1 f 2 t   Z 2 f 2 t   2 Z1 f1 t 
f 2 t 
2 Z1
t

f1 t  Z1  Z 2
transmission
coefficient
Into more dense medium
Into less dense medium
1   2
1   2
Impedance Matching: No Reflection!
Z1  Z 2
T11  T11
(not really an interface)
T11  T2  2