Download m - Cloudfront.net

Engineering Physics : Lecture 10
(Chapter 7 Halliday)



Work done by variable force
 Spring
Problem involving spring & friction
Work done by variable force in 3-D
 Newton’s gravitational force
Physics : Lecture 10, Pg 1
Review: Constant Force...
W = F d

No work done if  = 90o.
 No
work done by T.
T
v
 No
work done by N.
v
N
Physics : Lecture 10, Pg 2
Review: Work/Kinetic Energy Theorem:
{Net Work done on object}
=
{change in kinetic energy of object}
WF = K = 1/2mv22 - 1/2mv12
v1
v2
F
m
WF = Fx
x
Physics : Lecture 10, Pg 3
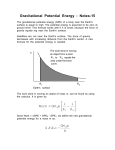
Work done by Variable Force: (1D)


When the force was constant, we
wrote W = F x
 area under F vs. x plot:
F
Wg
x
x
For variable force, we find the area
by integrating:
 dW = F(x) dx.
F(x)
x2
W   F ( x) dx
x1
x1
dx
x2
Physics : Lecture 10, Pg 4
Work/Kinetic Energy Theorem for a
Variable Force
x2
W   F dx
x1
x2
m
x1
v2
dv dx
dt
mv
v1
F  ma  m dv
dt
dv dx dv
dv
=
= v dx (chain rule)
dt
dt dx
dv
dx
dx
v2
 m  v dv
v1
1
1
1
 m (v22 v12 )  m v22  m v12  ΔKE
2
2
2
Physics : Lecture 10, Pg 5
1-D Variable Force Example: Spring

For a spring we know that Fx = -kx.
F(x)
x1
x2
x
relaxed position
-kx
F = - k x1
F = - k x2
Physics : Lecture 10, Pg 6
Spring...

The work done by the spring Ws during a displacement
from x1 to x2 is the area under the F(x) vs x plot between
x1 and x2.
F(x)
relaxed position
x1
x2
x
Ws
-kx
Physics : Lecture 10, Pg 7
Spring...

The work done by the spring Ws during a displacement
from x1 to x2 is the area under the F(x) vs x plot between
x1 and x2.
x2
 F ( x)dx
Ws 
F(x)
x1
x1
x2
x
Ws
-kx

x2
 (kx)dx
x1
1
  kx2
2
Ws  

x2
x1
1
k x22  x12
2

Physics : Lecture 10, Pg 8
Work & Energy

A box sliding on a horizontal frictionless surface runs into a fixed
spring, compressing it a distance x1 from its relaxed position while
momentarily coming to rest.
 If the initial speed of the box were doubled and its mass were
halved, how far x2 would the spring compress ?
(a)
x2  x1
(b)
x2  2 x1
(c)
x2  2 x1
x
Physics : Lecture 10, Pg 9
Solution

Again, use the fact that WNET = K.
WNET = WSPRING = -1/2 kx2
K = -1/2 mv2
In this case,
and
so kx2 = mv2
v1
In the case of x1
x1  v1
m1
k
x1
m1
m1
Physics : Lecture 10, Pg 10
xv
m
k
Solution
So if v2 = 2v1 and m2 = m1/2
x 2  2 v1
m1 2
2m1
 v1
k
k
x 2  2 x1
v2
x2
m2
m2
Physics : Lecture 10, Pg 11
Problem: Spring pulls on mass.

A spring (constant k) is stretched a distance d, and a mass m
is hooked to its end. The mass is released (from rest). What
is the speed of the mass when it returns to the relaxed
position if it slides without friction?
m
relaxed position
m stretched position (at rest)
d
m
after release
v
m
back at relaxed position
vr
Physics : Lecture 10, Pg 12
Problem: Spring pulls on mass.

First find the net work done on the mass during the motion
from x = d to x = 0 (only due to the spring):




1 2 2
1 2
1 2
2
Ws   k x2  x1   k 0  d  kd
2
2
2
m stretched position (at rest)
d
m
vr
relaxed position
i
Physics : Lecture 10, Pg 13
Problem: Spring pulls on mass.

Now find the change in kinetic energy of the mass:
1 2 1 2 1 2
ΔK  mv 2  mv 1  mv r
2
2
2
m stretched position (at rest)
d
m
vr
relaxed position
i
Physics : Lecture 10, Pg 14
Problem: Spring pulls on mass.

Now use work kinetic-energy theorem: Wnet = WS = K.
1 2 1
kd  mv r 2
2
2
vr  d
k
m
m stretched position (at rest)
d
m
vr
relaxed position
i
Physics : Lecture 10, Pg 15
Problem: Spring pulls on mass.


Now suppose there is a coefficient of friction  between the
block and the floor
The total work done on the block is now the sum of the work
done by the spring WS (same as before) and the work done by
friction Wf.
.
Wf = f Δr = - mg d
r
m stretched position (at rest)
d
m
vr
f = mg
relaxed position
i
Physics : Lecture 10, Pg 16
Problem: Spring pulls on mass.

Again use Wnet = WS + Wf = K
WS 
Wf = -mg d
1 2
kd
2
1 2
1 2
kd  mgd  mvr
2
2
1 2
K  mvr
2
k 2
vr 
d  2 μgd
m
r
m stretched position (at rest)
d
m
vr
f = mg
relaxed position
i
Physics : Lecture 10, Pg 17
Work by variable force in 3-D:

Work dWF of a force F acting
through an infinitesimal
displacement dr is:
F
dr
.
dW = F dr

The work of a big displacement through a variable force will
be the integral of a set of infinitesimal displacements:

.
WTOT = F dr
Physics : Lecture 10, Pg 18
Work by variable force in 3-D:
Newton’s Gravitational Force

Work dWg done on an object by gravity in a displacement dr is
given by:
.
.
^
^ (dR r^ + Rd)
dWg = Fg dr = (-GMm / R2 r)
dWg = (-GMm / R2) dR
.
.
(since r^ ^ = 0, r^ r^ = 1)
^
dR
Rd
Fg

dr
m
r^
d
R
M
Physics : Lecture 10, Pg 19
Work by variable force in 3-D:
Newton’s Gravitational Force

Integrate dWg to find the total work done by gravity in a “big”
displacement:

R2

R2
Wg = dWg = (-GMm / R2) dR = GMm (1/R2 - 1/R1)
R1
R1
Fg(R2)
m
R2
Fg(R1)
R1
M
Physics : Lecture 10, Pg 20
Work by variable force in 3-D:
Newton’s Gravitational Force

Work done depends only on R1 and R2, not on the path taken.
 1
1 
Wg  GMm
 
 R2 R1 
m
R2
R1
M
Physics : Lecture 10, Pg 21
Newton’s Gravitational Force
Near the Earth’s Surface:

Suppose R1 = RE and R2 = RE + y
 R  R1 
  R  y    R E  
 GM
  GMm E
   m 2
Wg  GMm 2
 R1 R2 
 RE  y RE  
 RE
but we have learned that
So:
 GM

 R2
E


y



g

Wg = -mgy
m
RE+ y
RE
M
Physics : Lecture 10, Pg 22
Recap of today’s lecture







Review
Work done by gravity near the Earth’s surface
Examples:
 pendulum, inclined plane, free fall
Work done by variable force
 Spring
Problem involving spring & friction
Work done by variable force in 3-D
 Newton’s gravitational force
Look at textbook problems
Physics : Lecture 10, Pg 23