Download PHYSICS 51: Introduction

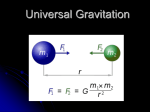
PHYSICS 50: Lecture 11.2
RICHARD CRAIG
Homework #11

Chapter 12



We will skip 12.8
12.3, 12.13, 12.23, 12.54, 12.55
Due Tuesday April 22
Newton’s Law of Gravitation



There is a force of attraction between any
two masses
F = Gm1m2/R2
G is a universal constant



G = 6.67 x 10-11Nm2/kg2
For spherical shapes all the mass acts as if
its at the center of the sphere (when outside
the sphere)
For multiple masses add the gravitational
forces as vectors
Escape Velocity

If an object has enough kinetic energy to overcome
the gravitational potential energy it can escape from
the gravitational pull

1/2 mv2 > GmM/R
or
V > (2GM/R)1/2
Escape velocity
Satellite motion
General Orbit is an ellipse… We will study the special case of a circle
Consider satellite orbits
Condition for a circular orbit
Gravitational Force = Centripetal Force
GMm/R2 = mv2/R
or Period of Circular orbit
T = 2R3/2/(GM)1/2
Circular Orbit Examples



Low Earth Orbit (LEO)
Geosynchronous orbit
Moon
Introduction

If you look to the right,
you’ll see a time-lapse
photograph of a simple
pendulum. It’s far from
simple, but it is a great
example of the regular
oscillatory motion we’re
about to study.
Describing oscillations

The spring drives the
glider back and forth
on the air-track and
you can observe the
changes in the freebody diagram as the
motion proceeds from
–A to A and back.
Simple harmonic motion
Real Spring
Ideal Spring (Hooke’s Law)
Simple Harmonic Motion
Force Equation
Equation of motion (2nd order differential equation)
General solution
With (definition of angular frequency)
SHM Solution
Special case with phi = 0
Simple harmonic motion viewed as a
projection