Download lecture3_stress1

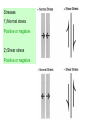
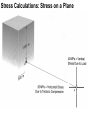
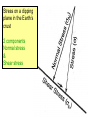
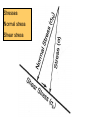
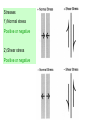
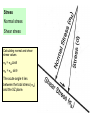
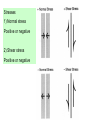
Dynamic Analysis:
The stresses that cause
deformation
The most important part of the text for the class is the
section on "stress calculations" (p. 110-114).
Spend some time with these calculations to convince
yourself that stress on a given plane resolves itself
into a single stress tensor.
Stresses
1) Normal stress
Positive or negative
2) Shear stress
Positive or negative
Responses to Stresses
1) Folding
2) Brittle faults
3) Ductile shear zones
4) Joints
Concept of Dynamic Analysis
The goals of dynamic analysis are:
1) Interpret the stresses responsible for deformation.
2) Describe the nature of the forces that cause the stresses.
3) Understand the relations between stress, strain and rock
strength.
Describing stress and force is a mathematical exercise.
Dynamic analysis is about the relations between the
stresses that cause deformation and the rock’s strength,
which tends to resist that deformation.
Force
Force: changes in the state of rest or motion of a body.
Only a force can cause a stationary object to move or change
the motion (direction and velocity) of a moving object.
force = mass x acceleration, F = ma,
mass = density x volume, m = rV,
therefore, r = m/V,
Weight is the magnitude of the force of gravity (g) acting upon a
mass.
The newton (N) is the basic (SI) unit of force.
1 newton = 1 kg meter/sec2
1 dyne = 1g cm/sec2 so 1 N = 105 dyne
1 pascal = newton/m2
Forces as Vectors
Force is a vector - it has magnitude and direction.
Vectors can be added and subtracted using vector
algebra. We can evaluate vectors in order to
determine whether the forces on a body are in
balance.
Load
Force
Forces in the Geologic World
Typically we think of the Earth as at rest - in static equilibrium,
or moving very slowly.
When there are net forces, they cause accelerations that are
usually one of 2 kinds:
1) slow ponderous motion of a tectonic plate that increases or
decreases velocity over a very long time, or;
2) sudden, short lived, strong accelerations during fault slip
accompanying earthquakes.
Two types of Forces
1) Body forces, that act on the mass of a body (gravity,
electromagnetic), and are independent of forces applied by
adjacent material, and;
2) Contact forces, are pushes and pulls across real or
imaginary surface of contact such as faults.
Three different type of loading due to contact forces:
1) gravitational loading - pushing on adjacent rock.
2) thermal loading - expansion or contraction.
3) displacement loading - push due to motion.
Stress (s)
Stress is force per unit area:
s = F/A
Units of Stress
1 newton = 1 kg meter/sec2 = this is a unit of force
1 dyne = 1g cm/sec2 so 1 N = 105 dyne
1 pascal = 1 newton/m2
= unit of stress
• 1 newton is about 0.224 809 pounds of force
• 1 dyne is about 2.248 x 10-6 pound of force
• 1 pascal is about 0.020 885 lb/ft2, thus pressure is measured in kPa
• 1 kPa = 0.145 lb/in2
• 9.81 Pa is the pressure caused by a depth of 1mm of water
Stress Underground (Pressure)
1) You are underground at
1000 meters depth.
2) Overlain by a huge cube of
granite (1 km x 1 km x 1 km)
3) Calculate stresses at the
base of the granite
4) Volume of block = 1000m x 1000m x 1000m
times
5) Density of the granite (r)= 2700 kg/m3
times
6) Acceleration due to gravity (g) = 9.8 m/s2
Stress Underground (Pressure)
The stress created by the weight of the
block of granite acting on the base of the
block is determined by dividing the force
(F) by the area (A = 1000m x 1000m)
s = F/A = 24,460,000 Pa = 24 MPa
This tells us about the lithostatic
stress gradient at depth.
F = 1000m x 1000m x 1000m x 2700 kg/m3 x 9.8 m/s2
s= F/A = 1000m x 1000m x 1000m x 2700 km/m3 x 9.8 m/s2
1000m x 1000m
Stress Underground (Pressure)
The stress created by the weight of the
block of granite acting on the base of the
block is determined by dividing the force
(F) by the area (A = 1000m x 1000m)
s = F/A = 24,460,000 Pa = 24 MPa
This tells us about the lithostatic
stress gradient at depth.
Shortcut, s = rgh =
2700 km/m3 x 9.8 m/s2 x 1000m = 26.5 Mpa
F = 1000m x 1000m x 1000m x 2700 kg/m3 x 9.8 m/s2
s= F/A = 1000m x 1000m x 1000m x 2700 km/m3 x 9.8 m/s2
1000m x 1000m
Stress Underground (Pressure)
s = 26.5 MPa
This tells us about the lithostatic
stress gradient at depth.
It increases 26.5 MPa per km,
equivalent to 265 bars or 0.265
kbar/km.
So for each 3.8 km depth, lithostatic
stress increase by 1 kbar or 100
MPa (same as under 10 km of ocean
water)
Stress is a Traction
To be more accurate, stress is a
traction. A traction is a stress
acting upon a surface.
'Stress' is a whole collection of
stresses acting upon on every
conceivable plane in every
conceivable orientation at an
infinitesimally small point (P).
From now on we will use the
term 'stress' when actually
referring to a 'traction'.
We will use the term 'stress
tensor' when referring to the
many tractions of stress
Stress Calculations: Stress on a Plane
Stress on a dipping
plane in the Earth’s
crust
2 components
Normal stress
&
Shear stress
Look inside granite at a plane that is inclined 65°.
Vertical s = 40 MPa,
Horizontal s = 20 MPa
What are the normal
and shear stresses
acting on the 65°
plane?
B. Block diagram of
dipping plane. What
are the total stresses
acting on the xz
plane, sxz?
D. Calculated stress values acting
C. Balance of forces acting
on the parcel of rock.
Components of stresses
acting on xz plane are:
parallel to x and z.
sz = 40 MPa,
Sz = 36.2 MPa and
sx = 20 MPa
Sx = 8.45 MPa
Sx and Sz, stress component
acting on the dipping plane
Sx = 20 MPa x area (cos 65°)
Sz = 40 MPa x area (sin 65°)
So, sxz2 = (Sx)2 + (Sz)2
= (8.4 MPa)2 + (36.2 MPa)2
= 37.2 MPa
Stresses
Normal stress
Shear stress
Stresses
1) Normal stress
Positive or negative
2) Shear stress
Positive or negative
We resolve stress into two
components
Normal stress, sn and the component
that is parallel to the plane, shear
stress, ss
1) Normal compressive stresses tend
to inhibit sliding along the plane and
are considered positive if they are
compressive.
2) Normal tensional stresses tend to
separate rocks along the plane and
values are considered negative.
3) Shear stresses tend to promote
sliding along the plane, labeled positive
if its right-lateral shear and negative if
its left-lateral shear.
Two components
of stress
The acute angle q
between sxz and plane
XZ is +78°.
The angle is positive,
measured clockwise from
plane to the stress
direction.
Numerical solution is easy.
sN = sxzsinq = 37 Mpa x sin78° = 36 Mpa
ss = sxzcosq = 37 Mpa x cos78° = 7.7 Mpa
20 MPa
Stress ellipsoid
If we plot all the stress vectors such that
their tails meet at a common point (the
point containing the planes for which we
originally computed the vectors, its
common point).
If we plot this to scale an elliptical
picture is generated, called the stress
ellipsoid.
It is useful for describing the state of
stress in any point within a body of rock.
Vector has magnitude and direction
The data are so systematic,
that if we plot all the stress
arrows, scaled properly, we
generate a stress ellipse.
The X and Y axes of the stress ellipse are called principal stress directions. They
are always mutually perpendicular.
The long axis is the axis of greatest principal stress, called s1.
The short axis is the axis of least principal stress, s3.
Theses two axes define the stress ellipse.
With a three dimensional analysis of stresses, we use a stress ellipsoid, here we
have an axis of intermediate stress, called s2. These are all mutually perpendicular.
The long axis is the axis of
greatest principal stress (s1) and
the short axis is the axis of least
principal stress (s3).
These axes define the stress
ellipse.
The intermediate principal stress
is oriented perpendicular to the
plane of s1 & s3 and is called s2.
The ellipse changes shape
depending on the values of the
principal stresses.
Hydrostatic Stress
If we calculate stress vectors within a
point of a hydrostatic stress field, we
find that the stress vectors have the
same value. Each stress vector is
oriented perpendicular to the plane.
All stress vectors are normal vectors,
they have no shear stress
components.
See p. 117, the special case of
Hydrostatic Stress.
Equal stress magnitudes in all
directions. Dive into a pool. All
stresses have the same values.
Hydrostatic stress = all principal
stresses in a plane are equal in all
directions. No shear stresses!
Hydrostatic Stress
Stress parallel to x and y axis is the
same, 12 MPa.
The single stress, s has a
magnitude of 12 MPa and is
oriented perpendicular to the
plane. This stress, s has no
shear stress.
Stress
We resolve stress into two
components.
Normal stress, sn and the
component that is parallel to the
plane, shear stress, ss.
sn can be compressive or tensile.
The X and Y axes of the stress ellipse
are called principal stress
directions. They are always mutually
perpendicular.
The long axis is the axis of greatest
principal stress, called s1.
The short axis is the axis of least
principal stress, s3.
Hydrostatic stress = all principal
stresses in a plane are equal in all
directions. No shear stresses!
Theses axes define the stress ellipse.
The Stress equations
We need the greatest
and least principal
stresses in order to
calculate normal and
shear stresses on any
given dipping plane
We can calculate the normal and shear stresses
on a plane of any orientation using these
equations.
Picture of vertical (sz) and horizontal stress (sx)
of 12 MPa. The lines are traces of planes at 5°
intervals. Stress for each plane have been
calculated. What is the state of stress?
Stress ellipse created by
arranging all the calculated
stresses (s) and arranging
them so their tips meet at a
point.
The length of each stress is
the same in hydrostatic state
of stress.
Stress ellipse created by arranging
all the calculated stresses (s) and
arranging them so their tips meet at a
point.
The length of each stress arrow is
different in non-hydrostatic state of
stress (differential stress).
Stress
Normal stress
Shear stress
Calculating normal and shear
stress values
sS = sxzcosq
sN = sxz sinq
The acute angle q lies
between the total stress (sxz)
and the XZ plane.
Stresses
1) Normal stress
Positive or negative
2) Shear stress
Positive or negative
The Stress equations
We need the greatest
and least principal
stresses in order to
calculate normal and
shear stresses on any
given dipping plane
We can calculate the normal and shear stresses on a plane of any
orientation using these equations.
sN = 40 MPa + 20 MPa - 40 Mpa – 20 Mpa (cos 60°) (where q = 30°)
2
2
sN = 30 Mpa – 10 MPa(0.5000) sN = 25 MPa
sS = 40 MPa – 20 MPa (sin 60°)
sS = 10 MPa (0.8660) sS = 8.6 MPa
Mohr Stress Diagram
a)This give us a useful picture or
diagram of the stress
equations.
b) They describe a circular focus
of paired values, sN & sS, the
normal and shear stresses that
operate on planes of any and
all orientations.
c) Using a Mohr stress diagram,
we can identify a plane of any
orientation relative to s1 and
read the values of normal (sN)
and shear stress (sS) acting on
the plane.
Principal normal values of
s1 & s3 are plotted on the
axis of the diagram.
A circle is drawn between
these two points, such
that s1 - s3 constitute the
circles diameter.
If s1 = 40 MPa and s3 = 20 MPa, all paired values of sN & sS exist for points on the
perimeter of the circle.
Use angle q=30°, with a radius on a unit circle, its 2 q equals 60°.
q is the angle between the greatest principal stress (s1) and the dip of the plane
Where the radius intersects the perimeter of the circle is a point whose x, y coordinates
are the sN & sS for the plane in question.
The center of the Mohr stress circle = mean stress (the hydrostatic
component of the stress field. Hydrostatic stress produces dilation.
The radius of the circle represents the deviatoric stress or the nonhydrostatic stress component. Deviatoric stress produces distortion.
The diameter of the circle represents differential stress. The large the
differential stress, the greater potential for distortion.
Angle q is the angle between
greatest stress component and
the plane.
Double the angle, plot as 2q
Mohr stress circle convention.
What is s1 and s3?
What is sn and ss?
And what’s the deal with
positive versus negative
values?
What is angle s?
It is the dip of the plane!
What is s1 and s3?
What is sn and ss?
And what’s the deal with
positive versus negative
values?
Various states of stress
Hydrostatic stress, a single point on
the Mohr circle that lies on the x-axis.
All normal stresses are the same,
and no shear stresses.
Uniaxial stress, two of the three
principal stresses are zero. The
circle passes thru the origin. The
part of the circle that lies to the right
of the shear stress axis is
compressive, to the left is tensile.
Axial stress, all three principal
stresses are non-zero, but two of the
principal stresses have the same
value. Typical stress ellipse.
Triaxial stress, all three principal
stresses are different.