Download 4-6 - mrhsluniewskiscience

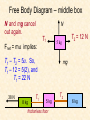
Objectives: The students will be
able to:
• Use the methods of vector algebra to
determine the net force acting on an
object.
• Draw an accurate free body diagram
locating each of the forces acting on an
object or a system of objects.
• Use free body diagrams and Newton's
laws of motion to solve word problems.
Review
http://www.youtube.com/watch?v=NYVMlmL0BPQ
Newton’s First Law:
Objects in motion tend to stay in motion
and objects at rest tend to stay at rest
unless acted upon by an unbalanced force.
Newton’s Second Law:
Force equals mass times acceleration
(F = ma).`
Newton’s Third
Law:
For every action there is an equal and
opposite reaction.
1stlaw: Homer is large and
has much mass, therefore he
has much inertia. Friction
and gravity oppose his
motion.
2nd law: Homer’s mass x
9.8 m/s/s equals his
weight, which is a force.
3rd law: Homer pushes
against the ground and it
pushes back.
Forces
• Newton’s Laws
of Motion
• Weight
• Free fall
• Force and motion
problems in 1-D
• Normal force
• Tension
• Free body diagrams
• Atwood device
• Static and kinetic
friction
• Coefficients of friction
• Air resistance
• Terminal velocity
Examples of Forces
• A force is just a push or pull. Examples:
– an object’s weight
– tension in a rope
– friction
– attraction between an electron and proton
• Bodies don’t have to be in contact to
exert forces on each other, e.g., gravity.
Fundamental Forces of Nature
• Gravity
– Attraction between any two bodies w/ mass
– Weakest but most dominant
• Electromagnetic
– Forces between any two bodies w/ charge
– Attractive or repulsive
• Weak nuclear force – responsible for
radioactive decay
• Strong nuclear force – holds quarks
together (constituents of protons and
neutrons)
4-6 Weight – the Force of Gravity;
and the Normal Force
Weight is the force exerted on an
object by gravity. Close to the
surface of the Earth, where the
gravitational force is nearly
constant, the weight is:
Sect. 4-6:Weight & Normal Force
Weight  The force of gravity on an object.
• Write as FG  W.
• Consider an object in free fall.
Newton’s 2nd Law is:
∑F = ma
• If no other forces are acting, only FG ( W) acts (in the
vertical direction).
∑Fy = may
Or:
(down, of course)
• SI Units: Newtons (just like any force!).
g = 9.8 m/s2  If m = 1 kg, W = 9.8 N
“Normal” Force
• Suppose an object is at rest on a table.
No motion, but does the force
of gravity stop? OF COURSE NOT!
• But, the object does not move:
2nd Law  ∑F = ma = 0
 There must be some other force acting
besides gravity (weight) to have ∑F = 0.
• That force  The Normal Force FN (= N)
“Normal” is a math term for perpendicular ()
FN is  to the surface & opposite to the weight
(in this simple case only!) Caution!!!
FN isn’t always = & opposite to the weight, as we’ll see!
Normal Force
• Where does the normal force
come from?
Normal Force
• Where does the normal force
come from?
• From the other object!!!
Normal Force
• Where does the normal force
come from?
• From the other object!!!
• Is the normal force ALWAYS
equal & opposite to the weight?
Normal Force
• Where does the normal force
come from?
• From the other object!!!
• Is the normal force ALWAYS
equal & opposite to the weight?
NO!!!
An object at rest must
have no net force on it. If it
“Free Body
Diagrams”
is sitting on a table, the force
of gravity is still there; what
other force is there? The
force exerted perpendicular
for Lincoln. Show
all forces in
proper directions.
to a surface is called the
Normal Force FN. It is
exactly as large as needed to
balance the force from the
object. (If the required force
gets too big, something breaks!)
∑F = ma = 0 or Newton’s 2nd Law for Lincoln:
FN – FG = 0 or FN = FG = mg
Note! FN & FG AREN’T action-reaction pairs from N’s 3rd Law! They’re
equal & opposite because of N’s 2nd Law! FN & FN ARE the action-
reaction pairs!!
Example 4-6
m = 10 kg
The normal
force is NOT
always equal &
opposite to the
weight!!
Find: Normal force on
box from table for Figs.
a., b., c. Always use
g N’s 2nd Law to
m CALCULATE FN!
Example 4-7
What happens when a m = 10 kg, ∑F = ma
person pulls upward on FP – mg = ma
the box in the previous 100 – 98 = 10a
a = 0.2 m/s2 m = 10 kg
example with a force
greater than the box’s
∑F = ma
weight, say 100.0 N?
The box will accelerate
FP – mg = ma
I upward because
FP > mg!!
Note: The normal force is zero here
because the mass isn’t in contact with
a surface!
Example 4-8: Apparent “weight loss”
A 65-kg woman descends in an elevator
that accelerates at 0.20g downward. She
stands on a scale that reads in kg.
(a) During this acceleration, what is her
weight & what does the scale read?
(b) What does the scale read when the elevator
descends at a constant speed of 2.0 m/s?
• Note: To use Newton’s 2nd Law for her, ONLY the forces
acting on her are included. By Newton’s 3rd Law, the
normal force FN acting upward on her is equal & opposite
to the scale reading. So, the numerical value of FN is equal
to the “weight” she reads on the scale! Obviously, FN here
is NOT equal & opposite to her true weight mg!!
How do we find FN? As always
We apply Newton’s 2nd Law to her!!
Normal force
• When an object lies on a table or on the
ground, the table or ground must exert
an upward force on it, otherwise gravity
would accelerate it down.
• This force is called the normal force.
N
In this particular case,
N = mg.
m
mg
So, Fnet = 0; hence a = 0.
Normal forces aren’t always up
“Normal” means perpendicular. A normal
force is always perpendicular to the contact
surface.
N
For example, if a
mg
flower pot is
setting on an
incline, N is not
vertical; it’s at a
right angle to the
incline. Also, in
this case, mg > N.
Normal force directions
• Up
– You’re standing on level ground.
– You’re at the bottom of a circle while flying a loopthe-loop in a plane.
• Sideways
– A ladder leans up against a wall.
– You’re against the wall on the “Round Up” ride
when the floor drops out.
• At an angle
– A race car takes a turn on a banked track.
• Down
– You’re in a roller coaster at the top of a loop.
Cases in which N  mg
1. Mass on incline
2. Applied force acting on the mass
3. Nonzero acceleration, as in an elevator
or launching space shuttle
FA
N
N
a
N
mg
mg
mg
When does N = mg ?
If the following conditions are satisfied,
then N = mg:
• The object is on a level surface.
• There’s nothing pushing it down or
pulling it up.
• The object is not accelerating vertically.
N and mg are NOT an Action-Reaction Pair!
N
“Switch the nouns to find the reaction partner.”
The dot represents the man.
m
mg, his weight, is the force on
the man due to the Earth.
mg
Fg
FE
Earth
FE is the force on the
Earth due to the man.
N, the normal force, is the force
on the man due to the ground.
Fg is the force on the
ground due to the man.
The red vectors are an action-reaction pair. So are the blue
vectors. Action-reaction pairs always act on two different bodies!
Box / Tension Problem
38 N
8 kg
T1
5 kg
T2
6 kg
frictionless floor
A force is applied to a box that is connected
to other boxes by ropes. The whole system
is accelerating to the left.
 The problem is to find the tensions in the
ropes.
 We can apply the 2nd Law to each box
individually as well as to the whole system.

Box / Tension Analysis
38 N
8 kg
T1
5 kg
T2
6 kg
frictionless floor
T1 pulls on the 8-kg box to the right just as
hard as it pulls on the middle box to the left.
 T1 must be < 38 N, or the 8-kg box couldn’t
accelerate.
 T2 pulls on the middle box to the right just as
hard as it pulls on the 6-kg box to the left.
 T1 must be > T2 or the middle box couldn’t
accelerate.

Free Body Diagram – system
N
For convenience, we’ll choose
left to be the positive direction.
The total mass of all three
boxes is 19 kg.
38 N
19 kg
N and mg cancel out.
Fnet = m a implies
a = 2.0 m/s2
mg
Since the ropes don’t
stretch, a will be 2.0 m/s2
for all three boxes.
Free Body Diagram – right box
N and mg cancel out.
For this particular box,
Fnet = ma implies:
N
T2
6 kg
T2 = 6a = 6(2) = 12 N.
(Remember, a = 2 m/s2 for all
three boxes.)
T1
38 N
8 kg
mg
5 kg
frictionless floor
T2
6 kg
Free Body Diagram – middle box
N and mg cancel
out again.
Fnet = m a implies:
N
T1
T1 – T2 = 5a. So,
T1 – 12 = 5(2), and
T1 = 22 N
38 N
8 kg
T1
T2 = 12 N
5 kg
mg
5 kg
frictionless floor
T2
6 kg
Free Body Diagram – left box
Let’s check our work
using the left box.
N
38 N
8 kg
T1 = 22 N
N and mg cancel out
here too.
Fnet = ma implies:
mg
38 - 22 = ma = 8(2).
16 = 16.
38 N
8 kg
T1
5 kg
T2
6 kg
Practice Problems
Practice #1: A fisherman yanks a fish out of the water with an acceleration of 3.5 m/s² using
very light fishing line that has a breaking strength of 28 N. The fisherman unfortunately loses
the fish as the line snaps. What can you say about the mass of the fish?
Practice #2: A 15.0-kg bucket is lowered by a rope in which there is 163 N of tension. What is
the acceleration of the bucket? Is it up or down?
Practice #3: An elevator (mass 6850 kg) is to be designed so that the maximum acceleration is
0.0780g. What are the maximum and minimum forces the motor should exert on the supporting
cable?
Practice #4: The cable supporting a 2001-kg elevator has a maximum strength of 21,750
N. What maximum upward acceleration can it gave the elevator without breaking?
Homework Chapter 4
• Problems #s 5, 13, 15, 17
Closure
• Kahoot