Download Chapter10_4-7_FA05

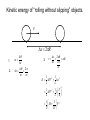
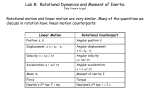
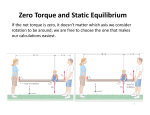
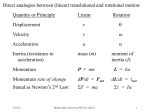
Rotational Motion
Chap. 10.4-7
NEW CONCEPT
‘Rotational force’: Torque
Torque is the “twisting force” that causes rotational motion. It
is equal to the magnitude of the component of an applied
force perpendicular to the arm transmitting the force.
F
R
A
The torque around point A is T = R x F
t=Ia
(compare to F = ma)
Example 10-6
Spinning Wheel
Solve using torque.
Then, using energy.
Example: torque’s in balance
2r
2m
4f
m
Figure 10-7
Angular and Linear Speed
Conceptual Checkpoint 10-1
How do the angular speeds compare?
V=rw
How do the linear speeds compare?
Figure 10-8
Centripetal and Tangential Acceleration
IMPORTANT:
For uniform circular motion,
The centripetal acceleration is:
v2
ac 
r
For constant angular speed, at = 0. Then,
the acceleration is RADIAL, inwards.
Figure 10-9
Rolling Without Slipping
Figure 10-11
Velocities in Rolling Motion
Figure 10-10
Rotational and Translational Motions of a Wheel
Figure 10-12
Kinetic Energy of a Rotating Object
K
1 2
mv
2
But… v  rw
So…
1 2
K  mv
2
1
2
 mrw 
2
1
 mr 2 w 2
2
 
Define the moment of inertia, I…
I  mr 2
K ROT
1 2
 Iw
2
(it’s different for different shapes!)
Figure 10-13
Kinetic Energy of a Rotating Object of Arbitrary Shape
I   mi ri
i
1 2
K  Iw
2
2
Figure 10-15
The Moment of Inertia of a Hoop
I   mi ri
2
i
All of the mass elements are at
the same radius, so….
I HOOP  mR
2
Figure 10-16
The Moment of Inertia of a Disk
I   mi ri
2
i
A disk is like a set of nested hoops.
With some algebra….
I DISK
1
2
 MR
2
Table 10-1a
Moments of Inertia for Uniform, Rigid Objects
of Various Shapes and Total Mass M
Conceptual Checkpoint 10-2
How does the moment of inertia
depend on the axis of rotation?
I = 2 (MR2)
I=M(2R)2=4MR2
Kinetic energy of rotating object
Total kinetic energy = Energy of translation plus energy of rotation.
Energy of translation: one-half m vee squared.
Energy of rotation: one-half I omega squared.
1 2 1 2
K  mv  Iw
2
2
A hoop and a disk roll without slipping with the same
speed. They have the same mass and radius. Is the kinetic
energy of the disk more, less or the same as the hoop?
V
V
1. The disk has more K than the hoop.
2. The disk has less K than the hoop.
3. The disk and the hoop have the
same K.
Kinetic energy of disk and hoop.
V
Disk and hoop have same mass,
radius, and velocity. How does K
compare?
V
The kinetic energy is given by:
K
1
1
MV 2  Iw 2
2
2
The only difference is the moment of inertia.
The disk has SMALLER moment of inertia
than the hoop. The further out the mass from
the axle, the higher the I.
Example 10-6
Spinning Wheel
Solve using torque.
Then, using energy.
Figure 10-24
Problem 10-60
Place your bets!
Ihoop = MR2
Idisk = ½ MR2
1. The disk reaches the bottom first.
2. The hoop reaches the bottom first.
3. They reach the bottom at the same time.
0 / 100
Who wins?
Both objects have the same potential energy, U = MGH.
More of the potential energy goes into rotational kinetic energy for
the hoop, because it has a larger moment of inertia. That leaves
less translational energy for the hoop, so it moves slower.
Kinetic energy of “rolling without slipping” objects.
V
x  2R
1.
2.

w
t
 2
t 

w
3.
v
x 2R

 wR
2
t
w
w
K
1
1
MV 2  Iw 2
2
2
1
1 V 
 MV 2  I  
2
2 R
1
I 
  M  2 V 2
2
R 
2
X-treme roller ball.
HINT: Consider conservation of energy. What
energy is changed into potential energy on the
frictionless side?
1. The ball reaches a greater height on the frictionless side.
2. The ball reaches a lower height on the frictionless side.
3. The ball goes to the same height.
X-treme roller ball explained.
At the bottom of the jump, the ball has both
translational and rotational energy. Some of the Lower!
potential energy U=MGH went into rotational
energy. On the frictionless side, the ball
continues to rotate, no rotational motion is
“lost”. So, there is less kinetic energy to change
into potential energy, or height.
Rolling down an inclined plane.
I
Note: Rolling friction is
STATIC friction!
Mgsin()
f
Forces acting on rolling body:
mg sin   f  ma
fR  Ia
Translation
Rotation
“Torque equals I times alpha”
For a rolling object:
v  Rw
a  Ra
a  a/R
mg sin   f  ma
a
f I 2
R
I 

mg sin   a m  2 
R 

Finally:
mg sin 
I
m 2
R
g sin 

1  I mR2
a
Rolling down an inclined plane, summary.
mg sin 
I
m 2
R
g sin 

1  I mR2
a
Mgsin()
f
Check the result:
If moment of inertia is zero, then we get the same result
as for sliding without friction.
The moment of inertia for symmetrical objects is in the form:
I = (number) X MR2
All objects with same SHAPE roll at same speed, independent of mass!!
Atwood Machine with Massive Pulley
Pulley with moment of inertia
I, radius R. Given M1, M2, and
H, what is the speed of M1
just before it hits the ground?
Strategy: Use conservation of mechanical energy.
Initial kinetic energy is 0. Initial potential energy is M1gH.
Final kinetic energy is translational energy of both blocks plus
rotational energy of pulley.
Final potential energy is M2gH.
Set final energy equal to initial energy.