* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Physics 121
Survey
Document related concepts
Transcript
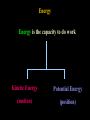
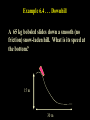
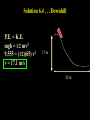
Physics 121 6. Work and Energy 6.1 Work 6.3 Kinetic Energy 6.4 Potential Energy 6.5 Conservative and Non-conservative forces 6.6 Mechanical Energy / Problem Solving 6.8 Conservation of Energy 6.9 Dissipative Forces / Problem Solving 6.10 Power Work Work = Force x Distance W=F.d Example 6.1 . . . Work for Slackers! You push a car with a force of 200 N over a distance of 3 m. How much work did you do? 200 N Solution 6.1 . . . Work for Slackers! W = F.d W = 200x3 W = 600 Nm W = 600 J Note: A Joule (J) is just another term for newton . meter (N m) Energy Energy is the capacity to do work Kinetic Energy Potential Energy (motion) (position) Kinetic Energy K.E. = 1/2 mv2 Example 6.2 . . . Kinetic Energy The K.E. of a car is 600 J and its mass is 1000 kg. What is its speed? Solution 6.2 . . . Kinetic Energy K.E. = 1/2 m v2 600 = 1/2(1000)(v2) v = 1.1 m/s Example 6.3 . . . Save your work! You lift a 2 kg book and put it on a shelf 3 meters high. (a) How much work did you do? (b) Was the work “lost”? Solution 6.3 . . . Save your work! (a) W = F.d W = mgh W = 2x10x3 W = 60 J (b) Work was stored as Potential Energy (hidden). So gravitational P.E. = mgh Example 6.4 . . . Downhill A 65 kg bobsled slides down a smooth (no friction) snow-laden hill. What is its speed at the bottom? 15 m 30 m Solution 6.4 . . . Downhill P.E. = K.E. mgh = 1/2 mv2 9,555 = (1/2)(65) v2 v = 17.1 m/s 15 m 30 m Example 6.5 . . . Sticky bobsled Suppose the speed of the bobsled was actually measured to be 14.8 m/s instead of 17.1 m/s (a) What could have caused that? (b) What was the work done by the bobsled against friction? Solution 6.5 . . . Sticky bobsled (a) Not all the P.E. was converted to K.E. because some work was lost (heat energy) in doing work against friction: P.E. = K.E. + Wf (b) mgh = 1/2 mv2 + Wf 9,555 = 1/2(65) (14.8)2 + Wf Wf = 2,436 J Stretching Springs Hooke’s Law: The amount of stretch is directly proportional to the force applied. F=kx Lab Experiment Slope = “k” F x Example 6.6 . . . Springy Spring The spring constant (k) of a spring is 20 N/m. If you hang a 50 g mass, how much will it stretch? Solution 6.6 . . . Springy Spring F=kx mg = kx (50 /1000)(9.8) = (20)(x) x = 2.5 cm Lab Experiment Example 6.7 . . . Body building How much work would you have to do to stretch a stiff spring 30 cm (k = 120 N/m)? “Solution” 6.7 . . . Body building W=F.d W = (kx)(x) W = kx2 W = (120)(0.3)2 W = 10.8 J X Correct Solution 6.7 . . . Body building W=F.d We must use the AVERAGE Force! W = (1/2)(kx)(x) W =1/2 kx2 W = (1/2)(120)(0.3)2 W = 5 .4 J P.E. of a Spring = 1/2 kx2 Example 6.8 . . . Lugging the Luggage What is the speed when the distance is 3 m? 40 N 10 kg Hawaii or Bust! 600 Solution 6.8 . . . Lugging the Luggage What is the speed when the distance is 3 m? F.d = 1/2 m v2 (40 cos 600)(3) = (1/2)(10)(v2) v = 3.5 m/s 40 N 10 kg Hawaii or Bust! Moral of the story W = (F)(d)(cos) 600 Conservative Forces If the work done against a force does not depend on the path taken then that force is called a conservative force. Examples are gravity and spring force. The total mechanical energy (P.E. + K.E.) will remain constant in this case. If the work done against a force depends on the path taken then that force is called a non-conservative force. Example is friction. The total mechanical energy (P.E. + K.E.) will not remain constant in this case. Vote Democrat . . . Just kidding! Example 6.9 . . . Playing with Power Power is the rate of doing work P=W/t A pump can lift at most 5 kg of water to a height of 4 m every minute. What is the power rating of this pump? Solution 6.9 . . . Playing with Power W = mgh W = (5)(10)(4) W = 200 J P=W/t P = 200 J / 60 s P = 3.3 J / s P = 3.3 W Note: Watt (W) is just another term for Joules / second (J / s) That’s all folks!