Download SHM Notes

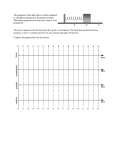
Plus Pendulums Revisited
Simple Harmonic Motion
 Oscillatory Motion (repeated motion)
 Only SHM if
 Oscillations are about an equilibrium position
 The restoring force is proportional to the object’s
displacement from equilibrium
 Examples include:
 Tacoma Narrows Bridge Collapse!

http://www.youtube.com/watch?v=ASd0t3n8Bnc
 Springs with masses on the end
 Pendulums with VERY small angles (< 10 degrees)
 For most pendulum motion we use energy or circular motion.
Consider a mass oscillating horizontally
across a frictionless surface:
For a, b, and c :
Label Fe, KE, EPE,
v, a, and x.
Numbers are not
required, except
for zeroes. You
may use max and
min to describe
quantities.
Horizontal Oscillating System (cont.)
 (b) This is defined as the equilibrium position, where
∆x=0, and as such has no net force. Fe=0
 According to Newton’s Second Law, net force is
proportional to acceleration. If net force here is zero,
then a=0
 When you stretch a spring, you give it elastic PE. When
you let it go, the EPE is converted to KE. At equilibrium
the spring has max KE
 KE=1/2mv2, so if KE is maximum at equilibrium, then I
also have max v (velocity)
Horizontal Oscillating System (cont.)
 (a) and (c) are almost identical in terms of these




quantities. At (a) the spring is stretched to its
maximum while still allowing it to oscillate. This is
called the amplitude (A). So, ∆x=+A
At (c) the spring is compressed the maximum amount
while still allowing for oscillation. This is the same
amplitude as (a). So, ∆x=-A
Hooke’s Law says Fe=-k∆x. If I apply what I know about
amplitude at either end, I get
(a) max Fe, pointing to the left
(b) max Fe, pointing to the right
Horizontal Oscillating System (cont.)
 (a) and (c) According to Newton’s Second Law, net
force is proportional to acceleration. If net force here is
at a maximum, then I have max a
 (a) and (c) At either end, while oscillating the mass
has to stop to return to equilibrium. At both ends v=0
 (a) and (c) At either end, if v=0, then I have no kinetic
energy. Elastic potential energy is EPE=1/2k∆x2 , so if
my spring is at maximum compression or stretched to
a maximum, I have max EPE
Frequency (f) vs Period (T)
Number of oscillations
per one second
Unit : Hertz (Hz)
osc
f 
time
Time for one oscillation
Unit : Seconds (s)
time
T
osc
These quantities are inverses, so…
1
f 
T
1
T
f
How to predict periods for oscillators:
 Pendulum:
l
T  2
g
 SHM (springs):
m
T  2
k
A 67 kg boy swings from a vine with a
period of oscillation on 2.34 seconds. What
is the length of the vine?
(Not PAP)A mass is allowed to oscillate on the end of a
spring of constant 140 N/m. If the mass oscillates with a
period of 1.26 seconds, what is the value of the mass?
(PAP) An 125N is hung on the end of a spring, stretching
it 23 cm. The mass is then replaced with an unknown
mass and allowed to oscillate. If the mass oscillates with
a period of 1.26 seconds, what is the value of the mass?
Do the following practice
problems:
 1. When a 55 g mass is attached to a spring, it makes
37 vibrations in 10.0 seconds. What is the system’s
frequency? What is its period?
 2. An unknown load oscillates from the end of a
spring, of constant 55 N/m, with a period of 6.58
seconds. What is the mass of the load?
 3. A mass oscillates horizontally at the end of a spring
of constant 85N/m. If the system has an amplitude of
11 cm, what is the maximum kinetic energy? What is
the maximum potential energy?