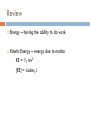Download Elastic Potential

ADV PHYSICS
Chapter 5
Sections 2 and 4
Review

Work – force applied over a given distance
W = F Δx
[W] = Joules, J
 Assumes
the force is constant
Review


Energy – having the ability to do work
Kinetic Energy – energy due to motion
KE = ½ mv2
[KE] = Joules, J
Review

Gravitational Potential Energy – energy an object
has due to its height
 Relative
to a reference point
GPE = mgh
[GPE] = Joules, J
Review

Mechanical energy – energy due to motion and/or
position
 Total
of KE and GPE
Elastic Potential Energy

Energy an object has due to its stretched or
compressed position
 Ex
– spring, rubber band
PEE = ½ kx2
k = spring constant
x = amount spring is stretched or compressed
[PEE] = Joules, J
Hooke’s Law


Whenever a spring is stretched or compressed, the
spring tries to pull itself back to its equilibrium
position
Restoring force – force that pulls a spring back to
equilibrium
 Greater
the stretch or compression, the greater the
restoring force
F = -kx
Hooke’s Law
F = -kx
F = restoring force
 x = amount spring is compressed or stretched
 Negative sign because the restoring force is always
opposite the direction of displacement, x
 k = spring constant

a number that indicates the stiffness of
(bigger the k, the stiffer the spring)
[k] = N/m
the spring
Sample Problem
1.
2.
If a mass of 0.55 kg attached to a vertical spring
stretches the spring 2 cm from its original
equilibrium position, what is the spring constant?
What if the spring is replaced with a spring that
stretches 36 cm from its equilibrium position.
What is the spring constant in this case?
Sample Problem
3.
4.
A slingshot consists of a light leather cup attached
between two rubber bands. If it takes a force of
32 N to stretch the bands 1.2 cm, what is the
equivalent spring constant of the rubber bands?
How much force is required to pull the cup 3 cm
from its equilibrium position?
Elastic Potential Energy and Work

Energy a spring has because its been stretched or
compressed
EPE = ½ kx2
To give a spring EPE requires work
 Can’t use W = FΔx since the force changes with
distance

W = ΔEPE = EPEf – EPEi
= ½ kxf 2 – ½ kxi 2
Conservation of Energy (Updated)

Energy Initial = Energy Final
ΣEi = ΣEf
PEei + PEgi + KEi = PEef + PEgf + KEf
½ kxi2 + mghi + ½ mvi2 = ½ kxf2 + mghf + ½ mvf2
where
PEe= Elastic Potential Energy
PEg= Graviational Potential Energy
KE= Kinetic Energy
Sample Problem
5.
A spring with a force constant of 5.2 N/m has a relaxed
length of 2.45 m. When a mass is attached to the end of
the spring and allowed to come to rest, the vertical length
of the spring is 3. 57 m. Calculate the elastic potential
energy stored in the spring.
Sample Problem
6.
A spring with a force constant of 50 N/m is to be
stretched from 0 to 20 cm.
(a) The work required to stretch the spring
from 10 to 20 cm is (1) more than,
(2) the same as, (3) less than that
required to stretch it from 0 to 10 cm.
(b) Compute the two work values.
Sample Problem
7.
A particular spring has a force constant of 2500 N/m.
(a) How much work is done in stretching
the relaxed spring by 6 cm?
(b) How much more work is done in
stretching the spring an additional 2 cm?
Sample Problem
8.
A 1.5 kg mass is placed on the end of a spring that has
a spring constant of 175 N/m. The mass-spring system
rests on a frictionless incline that is at an angle of 30
degrees from the horizontal. The system is eased into its
equilibrium position, where it stays.
(a) Determine the change in elastic potential
energy of the system.
(b) Determine the system’s change in
gravitational potential energy.
Challenge Problems
9.
A 0.250 kg block is pkaced on a light vertical spring (k =
5.00 x 103 N/m) and is pushed downwards, compressing
the spring 0.100 m. After the block is released, it leaves
the spring and continues to travel upwards.
(a)
What height above the point of release will the block reach
if air resistance is negligible?
(a)
What is the velocity of the block when it reaches the halfway
point (0.50 m) from where the spring was stretched to?
Challenge Problems
10.
A 1.5 kg mass is placed on the end of a spring that has a
spring constant of 175 n/m. The mass-spring system rests
on a frictionless incline that is at an angle of 30 degrees
from the horizontal. The soystem is eased into its
equilibrium system where it stays.
(a)
(b)
(c)
What is the distance the spring streches?
Determine the change in elastic potential energy of the
system.
Determine the system’s change in gravitational potential
energy.