Download ppt - SBEL - University of Wisconsin–Madison

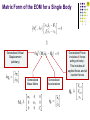
ME451
Kinematics and Dynamics
of Machine Systems
Dynamics: Review
November 4, 2013
Radu Serban
University of Wisconsin, Madison
2
Dynamics M&S
Dynamics Modeling



Formulate the system of equations that govern the time evolution of a
system of interconnected bodies undergoing planar motion under the
action of applied (external) forces
 These are differential-algebraic equations
 Called Equations of Motion (EOM)
Understand how to handle various types of applied forces and properly
include them in the EOM
Understand how to compute reaction forces in any joint connecting any
two bodies in the mechanism
Dynamics Simulation


Understand under what conditions a solution to the EOM exists
Numerically solve the resulting (differential-algebraic) EOM
3
Newton’s Laws of Motion

1st Law
Every body perseveres in its state of being at rest or of moving uniformly straight
forward, except insofar as it is compelled to change its state by forces impressed.

2nd Law
A change in motion is proportional to the motive force impressed and takes place
along the straight line in which that force is impressed.

3rd Law
To any action there is always an opposite and equal reaction; in other words, the
actions of two bodies upon each other are always equal and always opposite in
direction.

Newton’s laws



are applied to particles (idealized single point masses)
only hold in inertial frames
are valid only for non-relativistic speeds
Isaac Newton
(1642 – 1727)
Variational EOM for a Single Rigid Body
Newton’s EOM for a Differential Mass dm(P)

Apply Newton’s 2nd law to the differential mass 𝑑𝑚(𝑃) located at point P,
to get

This is a valid way of describing the motion of a body: describe the
motion of every single particle that makes up that body

However



It involves explicitly the internal forces acting within the body (these are
difficult to completely describe)
Their number is enormous
Idea: simplify these equations taking advantage of the rigid body assumption
5
6
The Rigid Body Assumption:
Consequences

The distance between any two points 𝑃 and 𝑅 on a rigid body is constant
in time:
and therefore

The internal force 𝐟𝑖 𝑃, 𝑅 𝑑𝑚 𝑃 𝑑𝑚(𝑅) acts along the line between 𝑃 and
𝑅 and therefore is also orthogonal to 𝛿(𝐫 𝑃 − 𝐫 𝑅 ):
7
Variational EOM for a Rigid Body
8
Principle of Virtual Work

Principle of Virtual Work
 If a system is in (static) equilibrium, then the net work done by external
forces during any virtual displacement is zero
 The power of this method stems from the fact that it excludes from the
analysis forces that do no work during a virtual displacement, in
particular constraint forces

D’Alembert’s Principle
 A system is in (dynamic) equilibrium when the virtual work of the sum
of the applied (external) forces and the inertial forces is zero for any
virtual displacement
 “D’Alembert had reduced dynamics to statics by means of his
principle” (Lagrange)

The underlying idea: we can say something about the direction of
constraint forces, without worrying about their magnitude
9
Virtual Displacements in terms of
Variations in Generalized Coordinates (1/2)
10
Virtual Displacements in terms of
Variations in Generalized Coordinates (2/2)
Variational EOM with Centroidal Coordinates
Newton-Euler Differential EOM
12
Variational EOM with Centroidal LRF
13
Variational EOM with Centroidal LRF
14
Differential EOM for a Single Rigid Body:
Newton-Euler Equations

The variational EOM of a rigid body with a centroidal body-fixed reference frame
were obtained as:

Assume all forces acting on the body have been accounted for.
Since 𝛿𝐫 and 𝛿𝜙 are arbitrary, using the orthogonality theorem, we get:


Important: The Newton-Euler equations are
valid only if all force effects have been
accounted for! This includes both applied
forces/torques and constraint forces/torques
(from interactions with other bodies).
Isaac Newton
(1642 – 1727)
Leonhard Euler
(1707 – 1783)
Virtual Work and Generalized Force
16
Calculating Generalized Forces

Nomenclature:
 𝐪
generalized accelerations
 𝛿𝐪
generalized virtual displacements
 𝐌
generalized mass matrix
 𝐐
generalized forces

Recipe for including a force in the EOM:
 Write the virtual work of the given force effect (force or torque)
 Express this virtual work in terms of the generalized virtual
displacements
 Identify the generalized force
 Include the generalized force in the matrix form of the variational EOM
17
Including a Point Force
18
Including a Torque
19
(TSDA)
Translational Spring-Damper-Actuator (1/2)

Setup

Compliant connection between points 𝑃𝑖 on body 𝑖 and 𝑃𝑗 on body 𝑗

In its most general form it can consist of:

A spring with spring coefficient 𝑘 and free length 𝑙0
A damper with damping coefficient 𝑐

An actuator (hydraulic, electric, etc.) which applies a force ℎ(𝑙, 𝑙, 𝑡)


The distance vector between points
𝑃𝑖 and 𝑃𝑗 is defined as
and has a length of
20
(TSDA)
Translational Spring-Damper-Actuator (2/2)

General Strategy

Write the virtual work produced by the force element in terms of an appropriate virtual
displacement
Note: positive 𝛿𝑙
separates the bodies
where
Hence the negative sign
in the virtual work
Note: tension defined as
positive

Express the virtual work in terms of the generalized virtual displacements 𝛿𝐪𝑖 and 𝛿𝐪𝑗

Identify the generalized forces (coefficients of 𝛿𝐪𝑖 and 𝛿𝐪𝑗 )
21
(RSDA)
Rotational Spring-Damper-Actuator (1/2)

Setup



Bodies 𝑖 and 𝑗 connected by a revolute joint at 𝑃
Torsional compliant connection at the common point 𝑃
In its most general form it can consist of:




A torsional spring with spring coefficient 𝑘 and
free angle 𝜃0
A torsional damper with damping coefficient 𝑐
An actuator (hydraulic, electric, etc.) which
applies a torque ℎ(𝜃𝑖𝑗 , 𝜃𝑖𝑗 , 𝑡)
The angle 𝜃𝑖𝑗 from 𝑥′𝑖 to 𝑥′𝑗
(positive counterclockwise) is
22
(RSDA)
Rotational Spring-Damper-Actuator (2/2)

General Strategy

Write the virtual work produced by the force element in terms of an appropriate virtual
displacement
Note: positive 𝛿𝜃
𝑖𝑗
separates the axes
where
Hence the negative sign
in the virtual work
Note: tension defined as
positive

Express the virtual work in terms of the generalized virtual displacements 𝛿𝐪𝑖 and 𝛿𝐪𝑗

Identify the generalized forces (coefficients of 𝛿𝐪𝑖 and 𝛿𝐪𝑗 )
Variational Equations of Motion for Planar Systems
24
Matrix Form of the EOM for a Single Body
Generalized Force;
includes all forces
acting on body 𝑖:
This includes all
applied forces and all
reaction forces
Generalized Virtual
Displacement
(arbitrary)
Generalized
Mass Matrix
Generalized
Accelerations
25
Variational EOM for the Entire System

Matrix form of the variational EOM for a system made up of 𝑛𝑏 bodies
Generalized Virtual
Displacement
Generalized
Force
Generalized
Mass Matrix
Generalized
Accelerations
Constraint Forces

Constraint Forces
 Forces that develop in the physical joints present in the system:
(revolute, translational, distance constraint, etc.)
 They are the forces that ensure the satisfaction of the constraints (they are
such that the motion stays compatible with the kinematic constraints)

KEY OBSERVATION: The net virtual work produced by the constraint forces
present in the system as a result of a set of consistent virtual displacements is
zero
 Note that we have to account for the work of all reaction forces present in the
system
 This is the same observation we used to eliminate the internal interaction
forces when deriving the EOM for a single rigid body

Therefore
provided q is a consistent virtual displacement
26
Consistent Virtual Displacements
What does it take for a virtual displacement to be consistent (with the set of
constraints) at a given, fixed time 𝑡 ∗ ?

Start with a consistent configuration 𝐪; i.e., a configuration that satisfies the
constraint equations:

A consistent virtual displacement 𝛿𝐪 is a virtual displacement which ensures that
the configuration 𝐪 + 𝛿𝐪 is also consistent:

Apply a Taylor series expansion and assume small variations:
27
28
Constrained Variational EOM
Arbitrary

Arbitrary
Consistent
We can eliminate the (unknown) constraint forces if we compromise to only
consider virtual displacements that are consistent with the constraint equations
Constrained Variational
Equations of Motion
Condition for consistent
virtual displacements
29
Lagrange Multiplier Theorem
Joseph-Louis
Lagrange
(1736– 1813)
30
Mixed Differential-Algebraic EOM
Constrained Variational
Equations of Motion
Condition for consistent
virtual displacements
Lagrange Multiplier Form
of the EOM
31
Lagrange Multiplier Form of the EOM

Equations of Motion

Position Constraint Equations

Velocity Constraint Equations

Acceleration Constraint Equations
Most Important Slide in ME451
Initial Conditions
Reaction Forces
33
Initial Conditions
34
Reaction Forces
Numerical Integration
Basic Concept

IVP

In general, all we can hope for is approximating the solution at a sequence of discrete
points in time


Uniform grid (constant step integration)
Adaptive grid (variable step integration)

Basic idea: somehow turn the differential problem into an algebraic problem (approximate
the derivatives)

IVP in dynamics:

What we calculate are the accelerations
Oversimplifying, we get something like

This is a second-order DE which needs to be integrated to obtain velocities and positions

36
37
Simplest method: Forward Euler

Starting from the IVP

Use the simplest approximation to the derivative

Rewrite the above as
and use ODE to obtain
Forward Euler Method
with constant step-size ℎ
FE: Geometrical Interpretation

IVP

Forward Euler integration formula
38
39
Stiff Differential Equations

Problems for which explicit integration methods (such as Forward Euler)
do not work well
 Other explicit formulas: Runge-Kutta (RK4), DOPRI5, AdamsBashforth, etc.

Stiff problems require a different class of integration methods: implicit
formulas
 The simplest implicit integration formula: Backward Euler (BE)
BE: Geometrical Interpretation

IVP

Forward Euler integration formula

Backward Euler integration formula
40
41
Forward Euler vs. Backward Euler
42
Stability of a Numerical Integrator

The problem:

How big can the integration step-size ℎ be without the numerical solution
blowing up?

Tough question, answered in a Numerical Analysis class

Different integration formulas, have different stability regions

We would like to use an integration formula with large stability region:


Example: Backward Euler, BDF methods, Newmark, etc.
Why not always use these methods with large stability region?

There is no free lunch: these methods are implicit methods that require the
solution of an algebraic problem at each step
43
Accuracy of a Numerical Integrator



The problem:

How accurate is the formula that we are using?

If we decrease ℎ, how will the accuracy of the numerical solution improve?

Tough question, answered in a Numerical Analysis class
Examples:

Forward and Backward Euler: accuracy 𝒪(ℎ)

RK45: accuracy 𝒪 ℎ4
Why not always use methods with high accuracy order?

There is no free lunch: these methods usually have very small stability regions

Therefore, they are limited to using very small values of ℎ
44
Implicit Integration: Conclusions

Stiff problems require the use of implicit integration methods


Because they have very good stability, implicit integration methods allow for
step-sizes ℎ that could be orders of magnitude larger than those needed if
using explicit integration
However, for most real-life IVPs, discretization using an implicit
integration formula leads to another nasty problem:

To find the solution at the new time, we must solve a nonlinear algebraic
problem

This brings back into the picture the Newton-Raphson method (and its
variants)

We have to deal with providing a good starting point (initial guess), computing the
matrix of partial derivatives, etc.
Putting it all together: Mechanism Analysis
46
Dynamics Modeling & Simulation










We are given a mechanism…
Describe how we would model this mechanism. How many bodies? How many
GCs?
What kinematic constraints would we use? What is KDOF? Write down the
equations that model those constraints.
What external forces act on the mechanism? Write down the corresponding
generalized forces.
Assemble the resulting EOM.
What is the initial configuration? Write down the additional conditions used to
specify initial conditions. Calculate the initial positions and velocities.
Calculate the accelerations and Lagrange multipliers at the initial time.
How would you solve these equations?
Assuming we have the solution to the Dynamics problem, in particular the
Lagrange multipliers, calculate constraint reaction forces.
If the mechanism is kinematically driven, what is the interpretation of the constraint
forces/torques corresponding to a driver constraint?
47
Mechanism Analysis
48
Mechanism Analysis
Model
49
Mechanism Analysis:
Kinematics
Constraint Equations
Jacobian
Velocity Equation
Acceleration Equation
50
Mechanism Analysis:
Generalized Forces
51
Mechanism Analysis:
Equations of Motion
Lagrange Multiplier Form
of the EOM
52
Mechanism Analysis:
DAEs
EOM
Constraint Equations
Velocity Equation
Acceleration Equation
53
Mechanism Analysis:
Position ICs

Find a set of consistent initial conditions (ICs) so that the mechanism starts in
an “all stretched out” configuration, with body 1 having an angular velocity 𝜔0 .

Kinematic constraint equations

Additional conditions (for position ICs)

Solve for the initial positions
54
Mechanism Analysis:
Velocity ICs

Find a set of consistent initial conditions (ICs) so that the mechanism starts in
an “all stretched out” configuration, with body 1 having an angular velocity 𝜔0 .

Jacobian and velocity equation

Additional conditions (for position ICs)

Solve for the initial positions
55
Mechanism Analysis:
Accelerations and Lagrange Multipliers at Initial Time

The accelerations and Lagrange multipliers at the initial time can be directly obtained using the EOM and
acceleration equation (once consistent initial conditions for positions and velocities are available):
56
Mechanism Analysis:
Inverse Dynamics
57
Mechanism Analysis:
Inverse Dynamics
⇒
⇒
⇒
⇒
58
Mechanism Analysis:
Inverse Dynamics

The “reaction force” associated with the driver constraint provides the force/torque
required to impose the prescribed motion

Driver constraint and Jacobian blocks
⇒