* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download ppt - SBEL - University of Wisconsin–Madison
Survey
Document related concepts
Centripetal force wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Joseph-Louis Lagrange wikipedia , lookup
Numerical continuation wikipedia , lookup
Dynamic substructuring wikipedia , lookup
Dirac bracket wikipedia , lookup
First class constraint wikipedia , lookup
Hunting oscillation wikipedia , lookup
N-body problem wikipedia , lookup
Classical central-force problem wikipedia , lookup
Routhian mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Equations of motion wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Analytical mechanics wikipedia , lookup
Transcript
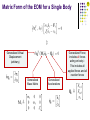
ME451 Kinematics and Dynamics of Machine Systems Dynamics: Review November 4, 2013 Radu Serban University of Wisconsin, Madison 2 Dynamics M&S Dynamics Modeling Formulate the system of equations that govern the time evolution of a system of interconnected bodies undergoing planar motion under the action of applied (external) forces These are differential-algebraic equations Called Equations of Motion (EOM) Understand how to handle various types of applied forces and properly include them in the EOM Understand how to compute reaction forces in any joint connecting any two bodies in the mechanism Dynamics Simulation Understand under what conditions a solution to the EOM exists Numerically solve the resulting (differential-algebraic) EOM 3 Newton’s Laws of Motion 1st Law Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed. 2nd Law A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed. 3rd Law To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction. Newton’s laws are applied to particles (idealized single point masses) only hold in inertial frames are valid only for non-relativistic speeds Isaac Newton (1642 – 1727) Variational EOM for a Single Rigid Body Newton’s EOM for a Differential Mass dm(P) Apply Newton’s 2nd law to the differential mass 𝑑𝑚(𝑃) located at point P, to get This is a valid way of describing the motion of a body: describe the motion of every single particle that makes up that body However It involves explicitly the internal forces acting within the body (these are difficult to completely describe) Their number is enormous Idea: simplify these equations taking advantage of the rigid body assumption 5 6 The Rigid Body Assumption: Consequences The distance between any two points 𝑃 and 𝑅 on a rigid body is constant in time: and therefore The internal force 𝐟𝑖 𝑃, 𝑅 𝑑𝑚 𝑃 𝑑𝑚(𝑅) acts along the line between 𝑃 and 𝑅 and therefore is also orthogonal to 𝛿(𝐫 𝑃 − 𝐫 𝑅 ): 7 Variational EOM for a Rigid Body 8 Principle of Virtual Work Principle of Virtual Work If a system is in (static) equilibrium, then the net work done by external forces during any virtual displacement is zero The power of this method stems from the fact that it excludes from the analysis forces that do no work during a virtual displacement, in particular constraint forces D’Alembert’s Principle A system is in (dynamic) equilibrium when the virtual work of the sum of the applied (external) forces and the inertial forces is zero for any virtual displacement “D’Alembert had reduced dynamics to statics by means of his principle” (Lagrange) The underlying idea: we can say something about the direction of constraint forces, without worrying about their magnitude 9 Virtual Displacements in terms of Variations in Generalized Coordinates (1/2) 10 Virtual Displacements in terms of Variations in Generalized Coordinates (2/2) Variational EOM with Centroidal Coordinates Newton-Euler Differential EOM 12 Variational EOM with Centroidal LRF 13 Variational EOM with Centroidal LRF 14 Differential EOM for a Single Rigid Body: Newton-Euler Equations The variational EOM of a rigid body with a centroidal body-fixed reference frame were obtained as: Assume all forces acting on the body have been accounted for. Since 𝛿𝐫 and 𝛿𝜙 are arbitrary, using the orthogonality theorem, we get: Important: The Newton-Euler equations are valid only if all force effects have been accounted for! This includes both applied forces/torques and constraint forces/torques (from interactions with other bodies). Isaac Newton (1642 – 1727) Leonhard Euler (1707 – 1783) Virtual Work and Generalized Force 16 Calculating Generalized Forces Nomenclature: 𝐪 generalized accelerations 𝛿𝐪 generalized virtual displacements 𝐌 generalized mass matrix 𝐐 generalized forces Recipe for including a force in the EOM: Write the virtual work of the given force effect (force or torque) Express this virtual work in terms of the generalized virtual displacements Identify the generalized force Include the generalized force in the matrix form of the variational EOM 17 Including a Point Force 18 Including a Torque 19 (TSDA) Translational Spring-Damper-Actuator (1/2) Setup Compliant connection between points 𝑃𝑖 on body 𝑖 and 𝑃𝑗 on body 𝑗 In its most general form it can consist of: A spring with spring coefficient 𝑘 and free length 𝑙0 A damper with damping coefficient 𝑐 An actuator (hydraulic, electric, etc.) which applies a force ℎ(𝑙, 𝑙, 𝑡) The distance vector between points 𝑃𝑖 and 𝑃𝑗 is defined as and has a length of 20 (TSDA) Translational Spring-Damper-Actuator (2/2) General Strategy Write the virtual work produced by the force element in terms of an appropriate virtual displacement Note: positive 𝛿𝑙 separates the bodies where Hence the negative sign in the virtual work Note: tension defined as positive Express the virtual work in terms of the generalized virtual displacements 𝛿𝐪𝑖 and 𝛿𝐪𝑗 Identify the generalized forces (coefficients of 𝛿𝐪𝑖 and 𝛿𝐪𝑗 ) 21 (RSDA) Rotational Spring-Damper-Actuator (1/2) Setup Bodies 𝑖 and 𝑗 connected by a revolute joint at 𝑃 Torsional compliant connection at the common point 𝑃 In its most general form it can consist of: A torsional spring with spring coefficient 𝑘 and free angle 𝜃0 A torsional damper with damping coefficient 𝑐 An actuator (hydraulic, electric, etc.) which applies a torque ℎ(𝜃𝑖𝑗 , 𝜃𝑖𝑗 , 𝑡) The angle 𝜃𝑖𝑗 from 𝑥′𝑖 to 𝑥′𝑗 (positive counterclockwise) is 22 (RSDA) Rotational Spring-Damper-Actuator (2/2) General Strategy Write the virtual work produced by the force element in terms of an appropriate virtual displacement Note: positive 𝛿𝜃 𝑖𝑗 separates the axes where Hence the negative sign in the virtual work Note: tension defined as positive Express the virtual work in terms of the generalized virtual displacements 𝛿𝐪𝑖 and 𝛿𝐪𝑗 Identify the generalized forces (coefficients of 𝛿𝐪𝑖 and 𝛿𝐪𝑗 ) Variational Equations of Motion for Planar Systems 24 Matrix Form of the EOM for a Single Body Generalized Force; includes all forces acting on body 𝑖: This includes all applied forces and all reaction forces Generalized Virtual Displacement (arbitrary) Generalized Mass Matrix Generalized Accelerations 25 Variational EOM for the Entire System Matrix form of the variational EOM for a system made up of 𝑛𝑏 bodies Generalized Virtual Displacement Generalized Force Generalized Mass Matrix Generalized Accelerations Constraint Forces Constraint Forces Forces that develop in the physical joints present in the system: (revolute, translational, distance constraint, etc.) They are the forces that ensure the satisfaction of the constraints (they are such that the motion stays compatible with the kinematic constraints) KEY OBSERVATION: The net virtual work produced by the constraint forces present in the system as a result of a set of consistent virtual displacements is zero Note that we have to account for the work of all reaction forces present in the system This is the same observation we used to eliminate the internal interaction forces when deriving the EOM for a single rigid body Therefore provided q is a consistent virtual displacement 26 Consistent Virtual Displacements What does it take for a virtual displacement to be consistent (with the set of constraints) at a given, fixed time 𝑡 ∗ ? Start with a consistent configuration 𝐪; i.e., a configuration that satisfies the constraint equations: A consistent virtual displacement 𝛿𝐪 is a virtual displacement which ensures that the configuration 𝐪 + 𝛿𝐪 is also consistent: Apply a Taylor series expansion and assume small variations: 27 28 Constrained Variational EOM Arbitrary Arbitrary Consistent We can eliminate the (unknown) constraint forces if we compromise to only consider virtual displacements that are consistent with the constraint equations Constrained Variational Equations of Motion Condition for consistent virtual displacements 29 Lagrange Multiplier Theorem Joseph-Louis Lagrange (1736– 1813) 30 Mixed Differential-Algebraic EOM Constrained Variational Equations of Motion Condition for consistent virtual displacements Lagrange Multiplier Form of the EOM 31 Lagrange Multiplier Form of the EOM Equations of Motion Position Constraint Equations Velocity Constraint Equations Acceleration Constraint Equations Most Important Slide in ME451 Initial Conditions Reaction Forces 33 Initial Conditions 34 Reaction Forces Numerical Integration Basic Concept IVP In general, all we can hope for is approximating the solution at a sequence of discrete points in time Uniform grid (constant step integration) Adaptive grid (variable step integration) Basic idea: somehow turn the differential problem into an algebraic problem (approximate the derivatives) IVP in dynamics: What we calculate are the accelerations Oversimplifying, we get something like This is a second-order DE which needs to be integrated to obtain velocities and positions 36 37 Simplest method: Forward Euler Starting from the IVP Use the simplest approximation to the derivative Rewrite the above as and use ODE to obtain Forward Euler Method with constant step-size ℎ FE: Geometrical Interpretation IVP Forward Euler integration formula 38 39 Stiff Differential Equations Problems for which explicit integration methods (such as Forward Euler) do not work well Other explicit formulas: Runge-Kutta (RK4), DOPRI5, AdamsBashforth, etc. Stiff problems require a different class of integration methods: implicit formulas The simplest implicit integration formula: Backward Euler (BE) BE: Geometrical Interpretation IVP Forward Euler integration formula Backward Euler integration formula 40 41 Forward Euler vs. Backward Euler 42 Stability of a Numerical Integrator The problem: How big can the integration step-size ℎ be without the numerical solution blowing up? Tough question, answered in a Numerical Analysis class Different integration formulas, have different stability regions We would like to use an integration formula with large stability region: Example: Backward Euler, BDF methods, Newmark, etc. Why not always use these methods with large stability region? There is no free lunch: these methods are implicit methods that require the solution of an algebraic problem at each step 43 Accuracy of a Numerical Integrator The problem: How accurate is the formula that we are using? If we decrease ℎ, how will the accuracy of the numerical solution improve? Tough question, answered in a Numerical Analysis class Examples: Forward and Backward Euler: accuracy 𝒪(ℎ) RK45: accuracy 𝒪 ℎ4 Why not always use methods with high accuracy order? There is no free lunch: these methods usually have very small stability regions Therefore, they are limited to using very small values of ℎ 44 Implicit Integration: Conclusions Stiff problems require the use of implicit integration methods Because they have very good stability, implicit integration methods allow for step-sizes ℎ that could be orders of magnitude larger than those needed if using explicit integration However, for most real-life IVPs, discretization using an implicit integration formula leads to another nasty problem: To find the solution at the new time, we must solve a nonlinear algebraic problem This brings back into the picture the Newton-Raphson method (and its variants) We have to deal with providing a good starting point (initial guess), computing the matrix of partial derivatives, etc. Putting it all together: Mechanism Analysis 46 Dynamics Modeling & Simulation We are given a mechanism… Describe how we would model this mechanism. How many bodies? How many GCs? What kinematic constraints would we use? What is KDOF? Write down the equations that model those constraints. What external forces act on the mechanism? Write down the corresponding generalized forces. Assemble the resulting EOM. What is the initial configuration? Write down the additional conditions used to specify initial conditions. Calculate the initial positions and velocities. Calculate the accelerations and Lagrange multipliers at the initial time. How would you solve these equations? Assuming we have the solution to the Dynamics problem, in particular the Lagrange multipliers, calculate constraint reaction forces. If the mechanism is kinematically driven, what is the interpretation of the constraint forces/torques corresponding to a driver constraint? 47 Mechanism Analysis 48 Mechanism Analysis Model 49 Mechanism Analysis: Kinematics Constraint Equations Jacobian Velocity Equation Acceleration Equation 50 Mechanism Analysis: Generalized Forces 51 Mechanism Analysis: Equations of Motion Lagrange Multiplier Form of the EOM 52 Mechanism Analysis: DAEs EOM Constraint Equations Velocity Equation Acceleration Equation 53 Mechanism Analysis: Position ICs Find a set of consistent initial conditions (ICs) so that the mechanism starts in an “all stretched out” configuration, with body 1 having an angular velocity 𝜔0 . Kinematic constraint equations Additional conditions (for position ICs) Solve for the initial positions 54 Mechanism Analysis: Velocity ICs Find a set of consistent initial conditions (ICs) so that the mechanism starts in an “all stretched out” configuration, with body 1 having an angular velocity 𝜔0 . Jacobian and velocity equation Additional conditions (for position ICs) Solve for the initial positions 55 Mechanism Analysis: Accelerations and Lagrange Multipliers at Initial Time The accelerations and Lagrange multipliers at the initial time can be directly obtained using the EOM and acceleration equation (once consistent initial conditions for positions and velocities are available): 56 Mechanism Analysis: Inverse Dynamics 57 Mechanism Analysis: Inverse Dynamics ⇒ ⇒ ⇒ ⇒ 58 Mechanism Analysis: Inverse Dynamics The “reaction force” associated with the driver constraint provides the force/torque required to impose the prescribed motion Driver constraint and Jacobian blocks ⇒