Download The demise of number ratios in music theory

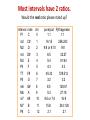
The demise of number
ratios in music theory
Pythagoras faces the final curtain
Richard Parncutt
Centre for Systematic Musicology
University of Graz, Austria
CIRMMT, Schulich School of Music
McGill University, Montreal
17 May 2012
Abstract
Medieval music theory was dominated by Pythagorean cosmic numerology. Today
there are still musicians, theorists, historians, composers, and psychologists out there
who theorize with number ratios. But most intervals have two ratios (Pythagorean
and just) that lie within a continuous range of acceptable tunings, so neither is
“correct”. Ratios only make psychological sense if the numbers correspond to audible
harmonics in complex tones (8:9 is ok but 64:81 is misleading). In fact, musical
intervals are approximate psychological distances on a linear, one-dimensional scale
that are determined by an aural cultural tradition. The relationship between intervals
and ratios is indirect and mediated by music history, performance constraints and
tone perception. Every tuning is a compromise among competing criteria: maximizing
harmonicity and familiarity, minimizing roughness (beating), optimizing stretch,
anticipating voice leading, manipulating expression. Modern performances of early
music (should) navigate between just and Pythagorean, as 12-tone equal
temperament does. Euler and Leibniz dreamed of a neural ratio detector, but modern
research revealed an inextricable mix of temporal and spectral (tonotopic) processing.
I will consider future implications for music theory and cognition.
Special thanks to composer Graham Hair, Professor Emeritus, Glasgow University and
Visiting Professor, Manchester Metropolitan University for ideas and feedback.
The major third interval
o Pythagorean tuning
reflects motion tendencies (leading tone rises)
emphasizes difference between major and minor
o Just tuning
minimizes beats between almost-coincident harmonics
Difference: 22 cents; cf. category width of “M3” = 100 cents
A rising major scale in 3 tuning systems
sound examples
• 12-tone equally tempered (12ET)
All semitones are equal
Works for any mainstream Western music
• Pythagorean (“3-limit”)
Combinations of P8=1:2 and P5 = 2:3
Occasional problems (enharmonic ambiguities)
• Just (“5-limit”)
Combinations of P8=1:2, P5 = 2:3, M3=4:5
Fifth between scale degrees 2 and 6 is not 2:3
Must constantly shift scale steps to stay in tune
A rising major scale in 3 tuning systems
ratios and cents
Scale step 2
3
4
5
6
7
8
12ET
200
400
500
700
900
1100
1200
Pythag
8 :9
204
64 :81 3 :4
408
498
2 :3
702
16 :27 128 :243 1 :2
906
1110
1200
Just
8 :9
4 :5
3 :4
2 :3
3 :5
8 :15
1 :2
204
386
498
702
884
1088
1200
Calculating ratios
Add intervals - multiply ratios
e.g. m7 = P5 + m3 = 3/2 x 6/5 = 9/5
– Pythagorean tuning
• combinations of P8 and P5 only
• frequency ratios in the form 2n/3m or 3m/2n
– Just tuning
• combinations of P8, P5, M3
Interval (cents) = log2 (f1/f2) x 1200
log2 (x) = log10 (x) / log10 (2) = ln (x) / ln (2)
Most intervals have 2 ratios.
Would the real ratio please stand up?
interval
P1
m2
M2
m3
M3
P4
TT
P5
m6
M6
m7
M7
P8
note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
chr.
0
1
2
3
4
5
6
7
8
9
10
11
12
pure/just Pythagorean
1:1
1:1
16:15
256:243
9:8 or 9:10
9:8
6:5
32:27
5:4
81:64
4:3
4:3
45:32
729:512
3:2
3:2
8:5
128:81
5:3
27:16
9:5 or 7:4
16:9
15:8
243:128
2:1
2:1
Some strange ideas of ratio theorists
Pythagoras
Greek philosopher and mathematician, 6th Century BC
Monochord mathematics
• P8 is 1:2, the P5 is 2:3, and the P4 is 3:4
• all other intervals by multiplying and dividing
• M3 is four P5s minus two P8s, or 64:81.
Music of the spheres
• planets and stars move according to this kind of math
• corresponding to musical notes  a cosmic symphony
• Pythagoras could hear it! (Tinnitus?)
Saint Bonaventure
Italian medieval theologian and philosopher, 1221 – 1274
“Since therefore, all things are beautiful and to some
measure pleasing; and [since] there is no beauty and
pleasure without proportion, and proportion is to be
found primarily in numbers; all things must have
numerical proportion. Consequently, number is the
principal exemplar in the mind of the Creator and as
such it is the principal trace that, in things, leads to
wisdom. Since this trace is extremely clear to all and is
closest to God, it … causes us to know Him in all
corporeal and sensible things; and while we learn that
things have numerical proportion, we take pleasure in
this numerical proportion and we judge things irrefutably
by virtue of the laws that govern it.”
Itinerarium mentis in Deum, II, 7
Boethius
Italian philosopher, early 6th century
“But since the nete synemmenon to
the mese (3,456 to 4,608) holds a
sesquitertian ratio -- that is, a
diatessaron -- whereas the trite
synemmenon to the nete
synemmenon (4,374 to 3,456) holds
the ratio of two tones....”
Fundamentals of Music, trans., Calvin Bower
(New Haven: Yale), IV, ix.
Cited by David Whitwell in Essays on the
Origins of Western Music
Giovanni Battista Benedetti
Italian mathematician, 1530 –1590
In a letter to Cipriano de Rore dated from around 1563,
Benedetti proposed a new theory of the cause
of consonance, arguing that since sound consists of air
waves or vibrations, in the more consonant intervals the
shorter, more frequent waves concurred with the longer,
more frequent waves at regular intervals. Isaac
Beeckman and Marin Mersenne both adopted this theory
in the next century.
(Wikipedia)
 What we now call a “temporal model” of consonance
Johannes Kepler
German mathematician, astronomer (1571-1630)
Third law of planetary motion:
• The square of the orbital period of a planet is directly
proportional to the cube of the semi-major axis of its orbit.
Aim:
• understand the music of the spheres
• express planetary motion in music notation
(Did he have tinnitus too?)
Sources
Holton, G. J., & Brush, S. G. (2001). Physics, the Human Adventure. Rutgers.
Burtt, E. A. (1954). Metaphysical Foundations of Modern Physical Science.
Gottfried Wilhelm Leibniz
German mathematician and philosopher (1646-1716)
The pleasures of subconscious counting
“Die Freude, die uns die Musik macht, beruht auf
unbewusstem Zählen.”
“Musik ist die versteckte mathematische Tätigkeit
der Seele, die sich nicht dessen bewusst ist, dass sie
rechnet.”
(Letters)
Leonhard Euler
Swiss mathematician and physicist (1707-1783)
“Take for example a clock, whose aim is to mark
divisions of time; we will like it most if … the parts are
laid out and combined in such a way that all contribute
to indicate time with exactitude. … where there is
perfection, there is necessarily also order.”
“…the degree of softness of ratio 1:pq, if p and q are
prime numbers … is p+ q - 1."
Tentamen novae theoriae musicae ex certissimis harmoniae
principiis dilucide expositae (1731)
(A attempt at a new theory of music, exposed in all clearness
according to the most well-founded principles of harmony)
Johanna Kinkel
German composer and writer (1810 –1858)
“As we wonder what it is that grips us with
foreboding and delight in Chopin’s music, we
are apt to find a solution that might appear to
many as pure fantasy, namely that Chopin’s
intention was to release upon us a cloud of
quarter-tones, which appear now as phantom
doppelgänger in the shadowy realm within
the intervals produced by enharmonic
change. Once the quarter-tones are
emancipated, an entirely new world of tones
will open to us.”
Acht Briefe an eine Freundin über Clavier-Unterricht
(1852)
Clarence Barlow
composer of electroacoustic music
“Harmonicity” of an interval
= “simplicity” of its number ratio
…which depends on “digestibility” of the numbers
…which depends on their prime factors
 Systematic enumeration of all possible frequency
ratios within an octave with relatively high harmonicity
 In order of interval size: 1:1, 15:16, 9:10, 8:9, 7:8, 6:7,
27:32, 5:6, 4:5, 64:81, 7:9, 3:4, 20:27, 2:3, 9:14, 5:8, 3:5,
16:27, 7:12, 4:7, 9:16, 5:9, 8:15, 1:2.
Two essays on theory. Computer Music Journal, 11, 44-59 (1987)
Laurel Trainor
(Music) Psychologist, McMaster University
“Effects of frequency ratio simplicity on
infants' and adults' processing of
simultaneous pitch intervals with
component sine wave tones” (abstract)
Effects of frequency ratio on infants' and adults'
discrimination of simultaneous intervals. Journal of
Experimental Psychology: Human Perception and
Performance, 23 (5), 1427-1438 (1997)
Ross W. Duffin
Dept of Music, Case Western Reserve U, Cleveland OH
“The fifth and fourth of 12ET aren’t bad, being out of
acoustical purity by only about one-fiftieth of a semitone,
but the major third is where 12ET fails the harmonic purity
test. 12ET major thirds are extremely wide – about oneseventh of a semitone wider than acoustically pure 5:4
major thirds. (…) This interval is the invisible elephant in
our musical system today. Nobody notices how awful the
major thirds are. (…) Asked about it, some people even
claim to prefer the elephant. (…) But I’m here to shake
those people out of their cozy state of denial. It’s the
acoustics, baby: Ya gotta feel the vibrations. “
How equal temperament ruined harmony (and why you should care).
London: Norton, 2007 (pp. 28-29)
Ross W. Duffin
“Some writers have also cast doubt on whether singers,
especially, could sound frequencies to the kind of tolerances
necessary to achieve intentional tuning choices. Performances
and recordings by modern early music groups, such as the Hilliard
Ensemble recording used below, refute that supposition utterly in
my opinion, presenting highly trained voices with minimal vibrato
and a level of accomplishment in tuning accuracy that Seashore,
Barbour and their colleagues probably never imagined.”
Just Intonation in Renaissance Theory and Practice. Music Theory Online (2006)
Robert (Bob) Fink
Saskatoon, Canada
“Historically, the ear has preferred simple ratios as harmonious,
and complex ratios have been avoided or considered noisy or
dissonant ... For example, two notes on the piano right next to
each other have a complex ratio (play them together to hear this)
and these kind of ratios cause ‘beats’ -- a kind of repetitive ‘wowwow-’ effect, which is physically measured as unpleasant to the
ear.”
On Music Origins, greenwych.ca/natbasis.htm
(N.B. this is NOT the Robert Fink at Dept. of Musicology, UCLA)
Kurt Haider
Institut für Musiktheorie und harmonikale
Grundlagenforschung, Wien
• eine mathematische Strukturwissenschaft … die historisch auf die
Pythagoreer, PLATON (427-347 v. Chr.) und die Neuplatoniker zurückgeht
• spätestens seit JOHANNES KEPLER (1571-1630) als empirische
Wissenschaft
• die harmonikale Naturphilosophie führt die Struktur der Naturgesetze auf
ganzzahlige Proportionen zurück
• die Reduktion auf das Messbare und Quantifizierbare, wie sie GALILEO
GALILEI (1564-1642) und JOHN LOCKE (1632-1704) vornahmen, (wird)
aufgehoben
• durch die Intervallempfindung der ganzzahligen Proportionen werden nun
qualitative Parameter wie Form, Gestalt oder Harmonie wieder
Gegenstand der Wissenschaften
kurthaider.megalo.at/node/49
The more “rational” opposition
Aristoxenus “Harmonics”
(4th Century BC; pupil of Aristotle)
“Mere knowledge of magnitudes does not enlighten one as to the
functions of the tetrachords, or of the notes, or of the differences
of the genera, or, briefly, the differences of simple and compound
intervals, or the distinction between modulating and nonmodulating scales, or the modes of melodic construction, or
indeed anything else of the kind.”
“we must not follow the harmonic theorists in their dense
diagrams which show as consecutive notes those which are
separated by the smallest intervals [but] try to find what intervals
the voice is by nature able to place in succession in a melody”
Macran, H. S. (1902). The harmonics of Aristoxenus. London: Oxford UP.
Jean-Philippe Rameau
(French composer and theorist, 1683 -1764)
Tried to explain major and minor triads using ratios:
• major triad
20:25:30 (4:5:6)
• Mm7
20:25:30:36
• minor triad
20:24:30 (10:12:15)
• m7
25:30:36:45
But then resorted to other means:
“Obviously there can be no complete chord without the
fifth, nor consequently without the union of two thirds
which form the fifth; for all chords should be based on
the perfect chord that results from this union.”
Treatise on Harmony (1722), transl. Philip Gossett (1971)
Rameau ‘s later work was based on the harmonic series - not ratios.
Hermann von Helmholtz
German physiologist and physicist, 1821-1894
“Even Keppler (sic.), a man of the deepest
scientific spirit, could not keep himself free from
imaginations of this kind … Nay, even in the most
recent times theorizing friends of music may be
found who will rather feast on arithmetical
mysticism than endeavor to hear out partial
tones” (p. 229).
On the Sensations of Tone as a Physiological Basis for the
Theory of Music, 1863; 4th ed. transl. A. J. Ellis
(Helmholtz theorized with ratios too…)
Carl Dahlhaus
German musicologist, 1928-1989
“Whereas in the ancient-medieval tradition number ratios were
considered to be the foundation or formal cause of consonance,
in modern acoustics and music theory they paled to an external
measure that says nothing about the essence of the matter. … In
the music theory of the 18th and 19th Centuries, the overtone
series is the natural archetype of the interval hierarchy upon
which rules of composition are founded. (But it was difficult to
explain autonomy of the minor triad and the dissonant character
of the fourth.) The surrender of the Platonic idea of number
meant nothing less than the collapse of the principle that had
carried ancient and medieval music theory; theory lost its object
of contemplation.”
C. Dahlhaus (Ed.), Einführung in die Systematische Musikwissenschaft (1988)
A short history of Western music theory
Central question and motivation:
Why is (Western) music meaningful and emotional?
1.
2.
3.
4.
Pythagoras, medieval theorists
Renaissance theory
Scientific revolution
Empirical psychology
Stages 2, 3 and 4 gradually moved away from Pythagoras
A short history of Western music theory
Pythagoras (6th Century BC)  Middle Ages
Musical intervals are number ratios
• Ratios are the “meaning of life, the universe
and everything” (Douglas Adams)
• All intervals are combinations of 1:2 and 2:3
Three kinds of “music”
• musica mundana — order of the cosmos
• musica humana — human-cosmic harmony
• musica instrumentalis — instrumental music
Boethius (6th C. AD) agreed in De Musica
A short history of Western music theory
Renaissance theorists
Ratios can also include factors of 5
 just M3 (4:5) preferred to Pythagorean (64:81)
•
•
•
•
Ramos de Pareja (1482)
Gioseffo Zarlino (1558)
Giovanni Battista Benedetti (1585)
etc.
(see Ross Duffin in MTO, 2006)
 Attempt to explain the sonority of omnipresent “triads”?
NB: No physical measurements of live performance!
A short history of Western music theory
Late scientific revolution (18th-19th century)
Musical intervals are audible relationships
between partials in harmonic complex tones
• 4:5 is distance between 4th and 5th harmonics
Consonance has two aspects:
• harmonicity (Rameau, Stumpf)
• roughness (Helmholtz)
Basis of intervals and consonance:
• physics of the natural environment
• physiology/psychology of perception
James Tenney’s
“Consonance-Dissonance Concepts”
CDC
concept
Tenney’s
definition
CDC-1
CDC-2
melodic affinity monophony
pitches in common
sonority of
early
isolated dyads polyphony
roughness or pitch
salience?
CDC-3
clarity of lower 14th C.
voice
pitch salience of (lower)
melody
CDC-4
property of
individual
tones in chord
dependence of
roughness on amplitude
of individual tones
CDC-5
smoothness or 19th C.
roughness
historical
period
18th C.
possible
perceptual account
roughness of whole
sonority
Only CDC-1 depends directly on ratios
A short history of Western music theory
20th century experiments on intonation
Summary of many experiments on intonation in
performance of tonal Western music:
• 12ET generally preferred
• Pythagorean tends to be preferred over just
– especially for rising leading tones
• Just intonation may be preferred for slow, steady
tones without vibrato
Many empirical studies! Authors:
Duke, Fyk, Green, Hagerman & Sundberg, O’Keefe, Loosen,
Karrick, Kopiez, Nickerson, Rakowski, Roberts & Matthews...
Johanna Devaney et al. (in prep.)
with Ichiro Fujinaga, Jon Wild, Peter Schubert, Michael Mandel
Participants: professional
Task: sing an exercise by Benedetti
(1585) to illustrate pitch drift in just
intonation
Main results:
• Intonation close to 12ET
• Standard deviation of pitch is
typically 10 cents (!)
• Small drift in direction of
Benedetti’s prediction
Ross W. Duffin
“ Renaissance performers would have preferred solutions that
favor just intonation wherever and whenever possible …
deviations from it would have been momentary adjustments to
individual intervals, rather than wholesale adoption of
temperament schemes”
Just Intonation in Renaissance Theory and Practice. Music Theory Online (2006)
Thomas Kuhn’s “paradigm shift”
or scientific revolution
Paradigm
•
•
Entire landscape of knowledge and implications in a discipline
Universally accepted
Long process of change
•
•
Gradual increase in number of anomalies  crisis
Experimentation with new ideas  intellectual battles
Features of change
•
•
Old and new are incommensurable
Shifts are more dramatic in previously stable disciplines
Examples
Physics: Classical mechanics  relativity and quantum mechanics
Psychology: Behaviorism  cognitivism
Music theory: Math & notation  performance & perception
Enharmonics
Are they related to ratios?
Assuming that G♯ is M3 above E, and A♭is M3 below C:
In Pythagorean tuning, G♯ > A♭
Because 64:81 is more than 400 cents
In just tuning, G♯ < A♭
because 4:5 is less than 400 cents
No clear relation between enharmonics and ratios!
Enharmonics
an example
Can we play this chord “like” a dominant 7th or “like” an inverted augmented 6th?
Or did Chopin simply make an innocent two-alternative forced choice?
And surely other issues of interpretation are much more important?
Enharmonics
origin of spelling conventions
Why do conventions of enharmonic spelling exist?
• Primarily to facilitate reading in performance
How do we facilitate reading?
• Minimize the number of symbols (clutter)
• Minimize the cognitive load by increasing the chance of
recognizing familiar patterns
How do we do that?
• Use key signatures for common (stable) tones
• Notate common intervals in consistent ways
12 semitones
 P8 not A7 or d9
7 semitones
 P5 not AA4 or d9
4 semitones
 M3 not AA2 or d4
This is a hierarchy: P8 is more important than P5 etc.
 Enharmonic spellings are often compromise solutions
Enharmonics
Why they exist
Guido’s diatonic staff has big advantages!
• Graphic:
• Compact:
• Efficient:
Illustrates melodic contour
7 rather than 12 vertical positions per octave
Common pitches easier to notate
Enharmonic equivalents exist because:
• A non-staff pitch can be notated two ways
• Scribes, composers had a “two-alternative forced choice”
 Don’t exaggerate importance of enharmonics!
 Don’t reify enharmonics!
Accuracy of interval sizes
How accurately can we perceive intonation?
Geringer & Madsen (1981). Discrimination between tone quality and
intonation in unaccompanied flute/oboe duets. Psychology of Music.
480 music and nonmusic graduate and undergraduate subjects listened
to 24 oboe and flute duets.
Variables:
• good/bad tone quality
• ET or one instrument shifted by 50 cents
Task:
• Intonation ok?
• Timbre ok?
Result:
Even musicians could not discriminate tone quality from intonation
This presumably applies also to Renaissance theorists!
Accuracy
How accurate are interval ratios in practice?
Uncertainty of interval sizes in middle register
• Just noticeable difference
– for successive pitches: about 2 cents (many studies)
– for simultaneous pitches: about 2 cents (audible beats)
• Added performance uncertainty for singers
– say: 3 cents for vocal jitter
– all voices have it! (old more than young)
• Combined uncertainty √(22 + 32) ≈ 4 cents
 A very conservative estimate for ideal conditions!
Much greater in most music.
Accuracy
Estimating the uncertainty of a given interval
Is the interval among first 10 harmonics?
Yes:
• If small and unambiguous, + 4 cents (larger: stretch?)
• If ambiguous, halve the difference between 2 possibilities
No:
Add uncertainties of simpler intervals (P8s and P5s)
Accuracy
An example
How uncertain is the size of the M2 interval?
Method 1: Direct from the harmonic series
Ambiguous: 8:9 (204 cents) or 9:10 (182 cents)?
 193 + 11 cents
Method 2: Add/subtract intervals
M2 = 2xP5 - P8
Uncertainty of P5 and P8 is about 4 cents each
(could be larger for P8 due to stretch of up to 10 cents!)
Combination of 3 intervals: add variances
 Square root of sum of squares
 √(42 + 42 + 42) = √48 ≈ 7 cents
Categorization of perceptual parameters
Color
e.g. range of wavelengths of the color red
– “nature”:
• physiology of rods and cones
– “nurture”:
• mapping between color words and light spectra
Speech sounds
e.g. range of formant frequencies of vowel /a/
– “nature”:
• vocal tract resonances near 500 and1500 Hz
– “nurture”:
• learned formant frequencies of each vowel
Experiment on categorical perception
of musical intervals
(Burns & Campbell, 1994)
P1 m2 M2 m3 M3 P4 TT P5 m6 M6 m7 M7 P8
Stimuli:
Melodic intervals
of complex tones;
all ¼ tones up to
one octave
Participants:
Musicians
Question:
name the interval
using regular
interval names
(semitones)
How the ear acquires pitch categories
…from the multimodal distribution of intervals in performed music
F
F#/Db
G
The ear is bombarded with interval sizes varying on a continuous scale,
(i) in complex tones (between partials) and (ii) in music (between fundamentals).
Some intervals are more common than others, so categories crystalize.
These psychological categories are the ORIGINAL, REAL “musical intervals”.
Distribution of interval sizes
Which do we find in the empirical data?
pure
Pythagorean
Bimodal distribution
with tendency toward
• pure (M3 = 386 cents) or
• Pythagorean (M3 = 408 cents)
NO: We never find this
Normal distribution
sd ≈ 20 cents
+ 1 sd = acceptable tuning
+ 2 sd = pitch category
YES: We generally find this
What influences intonation?
Real-time adjustment of tone frequency in performance
• Perceptual effects (individual tones)
– octave stretch (small intervals compressed*)
– beating of coinciding partials
• Cognitive effects (musical structure)
– preference for equally spaced categories (facilitates categorization
and cognitive processing)
– less stable tones are more variable in pitch**
– rising implication of leading tone; major-minor distinction
• Effects of performance
– solo versus accompaniment (soloists tend to play sharp)
– technical problems or limitations of instruments
• Effects of interpretation
– intended emotion (e.g. tension-release)
– intended timbre (e.g. deep = low)
* Rakowski
** Ambrazevicius & Wisniewska,
What about quartertones?
• Non-western theories of
frequency ratios are
equally problematic!
• Quartertones simply lie
between half-tone steps
Does the brain have a
ratio-detection device?
If it did, we might expect:
1. bimodal interval performance and preference distributions
2. low tolerance to mistuning of harmonics in complex tones
3. an evolutionary basis for ratio detection
In fact:
1. distributions are unimodal
2. harmonics mistuned by quartertone or semitone (!) are still
perceived as part of the complex tone (Moore et al., 1985)
3. environmental interaction depends instead on identification of
sound sources via synchrony, harmonicity… (Bregman, 1990)
Does the brain have a
ratio-detection device?
Is pitch perception based on frequency ratios between partials?
Decades of pitch research suggest that:
• the periodicity of a waveform plays a role within a critical band
• temporal processing is less important across critical bands
In both cases: no evidence for a ratio-detection device!
In general:
• Temporal and spectral processing (tonotopic representations) are
inextricably mixed in biological neural networks .
• Info about intervals is stored in this complex, hidden way, including
– distances between audible harmonics in isolated tones
– distances between tones in music
• The auditory system is very sensitive to such distances!
 separate foreground & background in everyday sounds (ASA)
Imagine a world without interval ratios
How could we explain the
beauty and power of
music without ratios?
A world without ratios
Psychological foundations
Innate ability to accurately perceive pitch distance
• Simultaneous: in harmonic complex tones
• Successive: between speech syllables
Ease of recognizing asymmetric patterns
• e.g. diatonic scales, major & minor triads
• for those with absolute pitch: character of keys
Tone/chord functions depend on vertical/horizontal context
• Not on notational conventions
Emotion & meaning due to layers of old associations
• Not magical mathematical or cosmic connections
A world without interval ratios
Imagine notating without accidentals…
12 approximately equally spaced pitch categories
• Idea is already latent in ancient Greek theory of tones and semitones
• inspired many 19-20th century “notation reforms”
In “keyboard
trigram” notation,
• staff lines are
groups of 3 black
keys
• leger lines are
groups of 2 black
keys
A world without interval ratios
Implications
Freedom to develop theories that
• depend on the listener`s subjective
experience (the music itself?)
• are independent of
– other theories
– notational conventions
A level field for comparing theories
• more objective comparison of theories
• a fresh look at
– history of notation and enharmonic spelling
– notational approaches of composers
A psychological theory of the
consonance of sonorities
• Smoothness of complex sounds
– peripheral, in ear (Helmholtz)
– lack of roughness, superficial
• Harmonicity of complex sounds
– central, in brain (Stumpf, Terhardt)
 clarity of harmonic function (Riemann)
• Familiarity, culture
– central, in brain
Roughness of pure tone dyads
Plomp & Levelt 1965
nothing to do with ratios
Roughness of complex tone dyads
Plomp & Levelt (1965)
ratios are artifacts of overlapping harmonics
Why is the tritone dissonant?
Not because of its ratio!
A tritone of pure tones sounds quite smooth
Dissonance of a tritone of complex tones:
• Roughness of almost coincident harmonics
• Inharmonicity
• Musical ambiguity
Harmonics of C3
Harmonics of F#2
The lot
So why do we still believe in ratios?
We prefer explanations that are:
1. Simple
• easy to understand, remember, apply
• easy to falsify (like a scientific theory)
2. Quantitative
• everyone can use words; maths needs expertise
• numbers seem more objective than words
• achievement s of science (Newton, Einstein…)
3. Phenomenological
• We can experience the theory directly
e.g. by retuning a keyboard and playing music
Why do we still believe in ratios?
We believe enharmonics are intrinsic to tonality
• and ratios are linked to enharmonics
E.g. musicians associate this music with sharps
• but non-musicians listen to the music itself
Why do we still believe in ratios?
We like music that is…
• consistent with our personal identity
• familiar but still interesting
• live, because
– played by real people (social function of music)
– like what we know (familiar) but also different (interesting)
– bond with audience members (identity)
Any slight retuning of a keyboard is:
• similar to what we know (familiar)
• but also different (interesting)
Why we still believe in ratios?
Post hoc ergo propter hoc – a logical fallacy
= after this, therefore because of this
= since event B followed event A, B must have been caused by A
Biological basis in classical conditioning
• ||: A = dog hears bell, then B = dog eats food :|| several times
• B predicts A  salivation
Human consequences
•
•
•
•
A rooster crows. We expect the sun to rise. Causation?
A solar eclipse. We play drums. The sun returns.
I just-tune my keyboard and enjoy the effect. ratio = causa?
cf. Huron`s “fast and dirty response” in Sweet anticipation
Why we still believe in ratios?
The word itself
• “ratio” is related to “rational” - we want “rational” explanations
• in fact, “ratio” originally means “reason”!
Online Etymological Dictionary
etymonline.com © 2001-2012 Douglas Harper
Ratio:
• 1630s, "reason, rationale,"
• from Latin ratio "reckoning, calculation, procedure," also "reason,"
• from rat-, pp. stem of reri "to reckon, calculate," also "think"
• mathematical sense is attested from 1660
Conclusions
Musical intervals are:
• primarily psychological (not physical or mathematical)
• approximate (categorical) – there is no ideal tuning
• learned from music (an aural tradition)
Exact musical interval size can depend on:
•
•
•
•
•
•
maximizing musical familiarity
maximizing harmonicity
minimizing roughness (fast beating)
optimizing stretch
anticipating voice leading
manipulating expression
The origin of musical emotion is:
• a chain of associations (many forgotten or subconscious)
• largely independent from the origin of intervals
Conclusions
• Advantages of ratio theory:
– theory accounts for most prevalent intervals
• octave, fifth, fourth, thirds, sixths, sevenths...
– theory explains12-tone equal temperament
• best approximation to main ratios
• Disadvantages of ratio theory:
–
–
–
–
–
two ratios for one interval? which is “correct”?
systematic deviations in real performance
unclear physiological or psychological basis
Intervals are subjective - part of culture
Intervals emerge/develop gradually over generations
We don‘t need ratios to explain…
Music’s meaning, beauty, magic
• chains of associations
Omnipresence of major and minor triads
• harmonicity, fusion, smoothness
Closure of harmonic cadences
• melodic distances, implied roots
Occasional poor tuning of piano accompaniments to solo violins
• octave stretch, leading tones, expression
Special character of Renaissance vocal music
• pitch structure, rhythm, timbre, expression
Success of some ratio-based microtonal composition (e.g. Partch )
• Form, development, timbre
Definition of music
• non-lexical, culturally complex sound-movement patterns
Further implications
Mathematics
is a tool for measuring things - not an aesthetic criterion
Pc-set theory
is applicable to any kind of music in the chromatic scale
Relatively wide major thirds
are more or less wide - not “Pythagorean”
New scales/tunings e.g. 19ET
their chance of success depends on similarity with familiar patterns
Implications for performance
of Renaissance polyphony
Some performers practice hard to approach just tuning - lately with
real-time computer feedback. What are they really achieving?
 Excellent skills in intonation, which improve performance regardless of
tuning.
x Suppression of natural tendencies to express by manipulating intonation.
Monteverdi would not have been impressed.
x Construction of an “authenticity” that may never have existed. Music
approaching JI has a special character, but without recordings of music as
performed in the Renaissance, we can only guess about its intonation.
x Exaggeration of the importance of music theory. 20th century theorists read
non-existent intentions into minds of 20th-century composers (think of those
complex pc-set analyses), so why should Renaissance theorists be any
different? They did not know what we know today, namely how difficult it is
to perform or perceive different tuning systems in practice.
Renaissance theorists were merely trying to explain the sonorous
Thanks
Graham Hair
Composer
Professor Emeritus, Glasgow University
Visiting Professor, Manchester Metropolitan University
The final curtain
http://www.youtube.com/watch?v=LL5YrVgZ_vU&feature=related