Download Galileo & Newton - Academic Computer Center

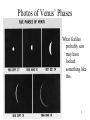
Galileo, Newton and the Birth of
Astrophysics
Galileo Galilei
• scientist and
outspoken supporter of
Copernicus’
heliocentric model
• lived and worked at
the time of Brahe and
Kepler
Galileo Galilei (1564-1642)
1
Galileo’s Physics Experiments
• Performed many
experiments on the motion
of falling bodies
• Showed that objects of
different mass dropped
from the same height will
fall to Earth at the same
time (neglecting air
resistance).
2
Galileo’s Telescope
• He was among the first to use
a telescope to observe the sky
and publish his observations.
• Observed:
– Mountains and valley on the
Moon (like Earth).
– Spots on the Sun and Solar
rotation (imperfect Sun).
– Phases of Venus
– Moons of Jupiter
Galileo’s drawings of the Moon
as seen through his telescope.
3
The Moons of Jupiter
A copy of Galileo’s original notes
showing Jupiter and four of its moons.
• The discovery of
these moons
proved that at least
some things did not
go around the
Earth.
• These 4 moons
were later named
the Galilean
satellites in honor
of Galileo.
4
Phases of Venus
Ptolemy’s
Earth-centered
model. Venus
moving along its
epicycle.
• We only can see
Venus due to
reflected sunlight
• We should only
see crescent
phases of Venus
if Venus went
around the Earth.
• Instead we see
Copernicus’
almost all of the
Sun-centered
model. Venus
phases. Venus
in orbit around
can’t orbit Earth.
the Sun.
5
Photos of Venus’ Phases
What Galileo
probably saw
may have
looked
something like
this.
6
Galileo and the end of Ptolemy’s
model
• By the end of Galileo’s
life Copernicus’ Suncentered model of the
Solar System and
Kepler’s Laws had
gained wider
acceptance.
• Galileo died almost 100
years after Copernicus
published his model
7
Isaac Newton (1642 - 1727)
• Newton was born the year
Galileo died.
• It had been believed that
there was one set of laws
that applied to Earth and
another set to the stars,
Moon and planets.
• Newton recognized that
there is one set of physical
laws that apply everywhere.
• The same force that causes
an apple to fall also keeps
Newton’s example showing how an
the Moon moving around
object with enough initial velocity
the Earth.
could be placed in orbit around Earth
8
Newton’s Achievements
• Considered the greatest physicist of
all time.
• Made significant contributions to
astronomy, physics and optics
• Invented the reflecting telescope
• Developed the branch of mathematics
called calculus
• His most famous contributions are to
the study of motion and gravity.
• He recognized that gravity was the
only force involved in keeping the
planets moving around the Sun
9
The Universal Law of Gravitation
• Every particle in the
Universe attracts every
other particle.
• The force is
proportional to the
product of their masses
and inversely
proportional to the
square of the distance
between them
10
Newton’s Laws
• 1st Law (Law of Inertia)
– A body at rest remains at
rest unless made to
change by a force
– A body in uniform
motion (in a straight line)
remains that way unless
made to change by forces
acting on it.
• Uniform motion means both
speed and direction are
unchanged
• A body not moving in a
straight line or not moving
at a constant speed must be
experiencing a force. 11
Acceleration
• Acceleration can be a change in speed (faster or
slower) or a change in direction
• You can experience an acceleration due to a force.
12
Mass and Weight are not the
same
• Mass - the amount of
matter a body
contains.
• Weight - a measure of
the gravitational force
on an object
• On the Moon we
would weigh less but
have the same amount
of mass
13
Newton’s Laws
• 2nd Law
– The amount of
acceleration (a)
that a force (F)
can produce
depends on the
mass (m) of the
object being
accelerated
a=F/m
14
Newton’s Laws
• 3rd law
– When two bodies
interact, they create
equal and opposite
forces on each other
– The force of gravity
the Earth experiences
due to the Sun is the
same as the force the
Sun experiences due to
the Earth.
15
Newton’s Version of Kepler’s 3rd Law
• Newton generalized Kepler’s 3rd Law so that it can be
applied anywhere in the Universe not just to planets
going around the Sun. (Remember P2(years) = a3(AU) ?)
• Newton’s version includes the mass of the two objects.
So if you know the period of the orbit and distance you
can determine the mass.
• By knowing the period of the orbit of one of Jupiter’s
moons and its distance from Jupiter you can “weigh”
Jupiter.
• We can use this formula to weigh anything (stars,
galaxies, black holes, etc.)
16
Surface Gravity
• Surface gravity is the acceleration a mass
undergoes at the surface of a celestial object (e.g.,
an asteroid, planet, or star)
• Surface gravity:
– Determines the weight of a mass at a celestial object’s
surface
• i.e., explains why you would weigh less on the Moon than on
the Earth.
– Influences the shape of celestial objects
– Influences whether or not a celestial object has an
atmosphere
Surface Gravity Calculations
• The surface gravity, denoted by g, is:
g = GM/R2
–
–
–
–
Where G is the gravitational constant
M is the mass of the object (planet, star, black hole)
R is the radius of the object
Massive, compact objects have greater surface gravity than
low-mass, large objects
• gEarth = 9.8 m/s2
• gEarth/gMoon = 5.6 and gJupiter/gEarth = 3
– On the Moon you would weigh 5.6 times less than you do
on Earth
– At Jupiter you would weigh three times more than you do
on Earth
Escape Velocity
• To overcome a celestial object’s gravitational
force and escape into space, a mass must obtain a
critical speed called the escape velocity
• Escape velocity:
– Determines if a spacecraft can move from one planet to
another
– Influences whether or not a celestial object has an
atmosphere
– Relates to the nature of black holes
Escape Velocity
Escape Velocity Calculation
• The escape velocity, Vesc, is determined from
Newton’s laws of motion and the Law of Gravity
and is given by:
Vesc = (2GM/R)1/2
where M and R are the mass and radius of the celestial
object from which the mass wishes to escape
• Notice dependence of Vesc on M and R, but not m
• Vesc,Earth = 11 km/s, Vesc,Moon = 2.4 km/s
Escape Velocity