* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 20
Rare Earth hypothesis wikipedia , lookup
History of astronomy wikipedia , lookup
Kepler (spacecraft) wikipedia , lookup
Planets beyond Neptune wikipedia , lookup
Extraterrestrial life wikipedia , lookup
Copernican heliocentrism wikipedia , lookup
Definition of planet wikipedia , lookup
Tropical year wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Equivalence principle wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Lunar theory wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Geocentric model wikipedia , lookup
First observation of gravitational waves wikipedia , lookup
Satellite system (astronomy) wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Astronomical unit wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
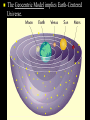
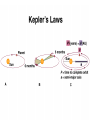
1. An industrial flywheel has a greater rotational inertia when most of its mass is (a) nearest the axis. (b) nearest the rim. (c) uniformly spread out as in a disk. 2. A ring and a disk both of the same mass, initially at rest, roll down a hill together. The one to reach the bottom first (a) is the disk. (b) is the ring. (c) both reach the bottom at the same time. 3. Put a pipe over the end of a wrench when trying to turn a stubborn nut on a bolt, to effectively make the wrench handle twice as long, you'll multiply the torque by (a) two. (b) four. (c) eight. Chapter 9 Gravity Newton’s law of gravitation Attractive force between all masses Proportional to product of the masses Inversely proportional to separation distance squared Explains why g=9.8m/s2 Provides centripetal force for orbital motion Newton’s Law of Universal Gravitation From Kepler's 3rd Law, Newton deduced inverse square law of attraction. Gm1m 2 F 2 d G=6.67 10-11 N m2/kg2 Gravity Questions Did the Moon exert a gravitational force on the Apollo astronauts? What kind of objects can exert a gravitational force on other objects? The constant G is a rather small number. What kind of objects can exert strong gravitational forces? Gravity Questions If the distance between two objects in space is doubled, then what happens to the gravitational force between them? What is the distance is tripled? …is quadrupled? What if the mass of one of the object is doubled? …tripled? …quadrupled? Weight and Weightlessness Weight » the force due to gravity on an object » Weight = Mass Acceleration of Gravity »W=mg “Weightlessness” - a conditions wherein gravitational pull appears to be lacking – Examples: » Astronauts » Falling in an Elevator » Skydiving » Underwater Ocean Tides The Moon is primarily responsible for ocean tides on Earth. The Sun contributes to tides also. What are spring tides and neap tides? Spring Tides Full Moon Earth New Moon Sun Neap Tides First Quarter Earth Last Quarter Sun BLACK HOLES Let’s observe a star that is shrinking but whose mass is remaining the same. What happens to the force acting on an indestructible mass at the surface of the star? SFA F F F m m 1 2 m1m2 F G 2 G Remember that the force between R 2 the two masses is given by R G G m1m2 R2 R m1m2 R2 R R R F G m1m2 R2 BLACK HOLES If a massive star shrinks enough so that the escape velocity is equal to or greater than the speed of light, then it has become a black hole. Light cannot escape from a black hole. Einstein’s Theory of Gravitation Einstein perceived a gravitational field as a geometrical warping of 4-D space and time. Near a Black Hole 4. Which is most responsible for the ocean tides? (a) ships (b) continental drift (c) the moon (d) the sun 5. If the sun were twice as massive (a) the pull of the earth on the sun would double. (b) its pull on the earth would double. (c) both of these. (d) neither of these 14. The car moving at 50 kilometers/hour skids 10 meters with locked brakes. How far will the car skid with locked brakes if it is traveling at 150 kilometers/hour? (a) 20 meters (b) 60 meters (c) 90 meters (d) 120 meters (e) 180 meters 16. When a car is braked to a stop, its kinetic energy is transformed to (a) stopping energy. (b) potential energy. (c) heat energy. (d) energy of rest. End of Chapter 9 Pythagoras (550 BC) Claimed that natural phenomena could be described by mathematics Aristotle (350 BC) Asserted that the universe is governed by physical laws The ancient Greeks believed that the earth was at the center of a revolving sphere with stars on it. The Geocentric Model implies Earth-Centered Universe. Copernicus (1500's) Developed a mathematical model for a Sun-centered solar system Tycho Brahe (1500's) Made precise measurements of the positions of the planets Kepler (1600's) Described the shape of planetary orbits as well as their orbital speeds Kepler’s First Law The orbit of a planet about the Sun is an ellipse with the Sun at one focus. Kepler’s Second Law A line joining a planet and the Sun sweeps out equal areas in equal intervals of time. Kepler’s Third Law The square of a planet's orbital period is proportional to the cube of the length of its orbit's semimajor axis. Or simply… T2 = R3 if T is measured in years and R is measured in astronomical units. An Astronomical Unit... …is the average distance of the Earth from the Sun. 1 AU = 93,000,000 miles = 8.3 lightminutes Kepler’s Laws These are three laws of physics that relate to planetary orbits. These were empirical laws. Kepler could not explain them. Kepler’s Laws...Simply (See page 192.) Law 1: Elliptical orbits… Law 2: Equal areas in equal times… Law 3: T2 = R3