* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Monday, October 27
International Ultraviolet Explorer wikipedia , lookup
Dyson sphere wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Star of Bethlehem wikipedia , lookup
Corona Borealis wikipedia , lookup
Extraterrestrial skies wikipedia , lookup
Canis Minor wikipedia , lookup
Observational astronomy wikipedia , lookup
Stellar kinematics wikipedia , lookup
Astronomical unit wikipedia , lookup
Stellar evolution wikipedia , lookup
Aries (constellation) wikipedia , lookup
Auriga (constellation) wikipedia , lookup
Cassiopeia (constellation) wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Corona Australis wikipedia , lookup
Star formation wikipedia , lookup
Canis Major wikipedia , lookup
Timeline of astronomy wikipedia , lookup
Cygnus (constellation) wikipedia , lookup
Perseus (constellation) wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
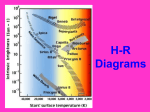
Introduction to Stars Stellar Parallax • Given p in arcseconds (”), use d=1/p to calculate the distance which will be in units “parsecs” • By definition, d=1pc if p=1”, so convert d to A.U. by using trigonometry • To calculate p for star with d given in lightyears, use d=1/p but convert ly to pc. • Remember: 1 degree = 3600” • Note: p is half the angle the star moves in half a year Our Stellar Neighborhood Scale Model • If the Sun = a golf ball, then – – – – – Earth = a grain of sand The Earth orbits the Sun at a distance of one meter Proxima Centauri lies 270 kilometers (170 miles) away Barnard’s Star lies 370 kilometers (230 miles) away Less than 100 stars lie within 1000 kilometers (600 miles) • The Universe is almost empty! • Hipparcos satellite measured distances to nearly 1 million stars in the range of 330 ly • almost all of the stars in our Galaxy are more distant Luminosity and Brightness • Luminosity L is the total power (energy per unit time) radiated by the star, actual brightness of star, cf. 100 W lightbulb • Apparent brightness B is how bright it appears from Earth – Determined by the amount of light per unit area reaching Earth – B L / d2 • Just by looking, we cannot tell if a star is close and dim or far away and bright Brightness: simplified • 100 W light bulb will look 9 times dimmer from 3m away than from 1m away. • A 25W light bulb will look four times dimmer than a 100W light bulb if at the same distance! • If they appear equally bright, we can conclude that the 100W lightbulb is twice as far away! Same with stars… • Sirius (white) will look 9 times dimmer from 3 lightyears away than from 1 lightyear away. • Vega (also white) is as bright as Sirius, but appears to be 9 times dimmer. • Vega must be three times farther away • (Sirius 9 ly, Vega 27 ly) Distance Determination Method • Understand how bright an object is (L) • Observe how bright an object appears (B) • Calculate how far the object is away: B L / d2 So L/B d2 or d √L/B Homework: Luminosity and Distance • Distance and brightness can be used to find the luminosity: L d2 B • So luminosity and brightness can be used to find Distance of two stars 1 and 2: d21 / d22 = L1 / L2 (since B1 = B2 ) i.e. d1 = (L1 / L2)1/2 d2 Homework: Example Question • Two stars -- A and B, of luminosities 0.5 and 2.5 times the luminosity of the Sun, respectively -- are observed to have the same apparent brightness. Which one is more distant? • Star A • Star B • Same distance Homework: Example Question • Two stars -- A and B, of luminosities 0.5 and 2.5 times the luminosity of the Sun, respectively -- are observed to have the same apparent brightness. How much farther away is it than the other? • LA/d2A = BA =BB = LB/d2B dB = √LB/LA dA • Star B is √5=2.24 times as far as star A The Magnitude Scale • A measure of the apparent brightness • Logarithmic scale • Notation: 1m.4 (smaller brighter) • Originally six groupings – 1st magnitude the brightest – 6th magnitude is 100x dimmer • So a difference of 5mag is a difference of brightness of 100 • Factor 2.512=1001/5 for each mag. Absolute Magnitude • The absolute magnitude is the apparent magnitude a star would have at a distance of 10 pc. • Notation example: 2M.8 • It is a measure of a star’s actual or intrinsic brightness called luminosity • Example: Sirius: 1M.4, Sun 4M.8 – Sirius is intrinsically brighter than the Sun Finding the absolute Magnitude • To figure out absolute magnitude, we need to know the distance to the star • Then do the following Gedankenexperiment: – In your mind, put the star from its actual position to a position 10 pc away – If a star is actually closer than 10pc, its absolute magnitude will be a bigger number, i.e. it is intrinsically dimmer than it appears – If a star is farther than 10pc, its absolute magnitude will be a smaller number, i.e. it is intrinsically brighter than it appears