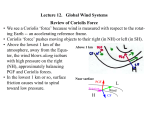
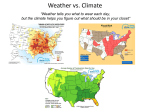
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Beams, Bursts, Bubbles, and Bullets: Relativistic Outflows in
Work (physics) wikipedia , lookup
Electromagnet wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Dark energy wikipedia , lookup
Woodward effect wikipedia , lookup
Lorentz force wikipedia , lookup
Nuclear structure wikipedia , lookup
Accretion disk wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Time in physics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Beams, Bursts, Bubbles, and Bullets: Relativistic Outflows in Astrophysics by Sebastian Heinz M.S., University of Colorado, 1997 A thesis submitted to the Faculty of the Graduate School of the University of Colorado in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Astrophysical and Planetary Sciences 2000 This thesis entitled: Beams, Bursts, Bubbles, and Bullets: Relativistic Outflows in Astrophysics written by Sebastian Heinz has been approved for the Department of Astrophysical and Planetary Sciences Prof. Mitchell C. Begelman Prof. Ellen G. Zweibel Date The final copy of this thesis has been examined by the signatories, and we find that both the content and the form meet acceptable presentation standards of scholarly work in the above mentioned discipline. Heinz, Sebastian (Ph.D.) Beams, Bursts, Bubbles, and Bullets: Relativistic Outflows in Astrophysics Thesis directed by Prof. Mitchell C. Begelman This thesis investigates the physics of relativistic outflows in astrophysical scenarios. We focus on collimated flows, known as jets, that occur in Active Galactic Nuclei (AGN) and Gamma-Ray Bursts (GRBs). The production and early propagation of relativistic jets is examined in the case of acceleration by dynamically dominant tangled magnetic fields. It is shown that such a configuration behaves in a similar fashion as a pure particle pressure dominated jet, however, it can avoid radiative losses and inverse Compton drag, which hamper particle dominated flows. The radiative signatures of such jets and several complications, such as dissipation of magnetic energy and radiation drag, are considered. To investigate the energetics and propagation of the kpc scale jet, we study the jet in the nearby galaxy M87. We find that the complex spectral behavior and the surprising correlation between radio brightness and the optical spectral index can be explained by simple adiabatic acceleration of the radiating particles. The lack of significant spectral evolution is consistent with magnetic fields below equipartition by a factor of a few. The impact of the enormous energy flux in the AGN jets on the large scale intergalactic environment is studied on the basis of a simple dynamical model. In general, the flow will displace the surrounding medium, leading to a depression in the X-ray surface brightness. We show how a grid of models can be used to infer important physical parameters, such as the average kinetic jet power from Chandra observations of radio galaxies embedded in clusters. Relativistic flows also occur in Gamma-Ray Bursts. It has generally been accepted that only models in which the gamma rays originate from internal variations in the flow (internal iv shocks) can explain the complex temporal signatures of GRBs. We present a new model, based on external dissipation of kinetic energy stored in dense bullets, that can also explain the millisecond variability seen in some bursts. The basic observational characteristics of such a model are presented, along with a preliminary analysis of the requirements that the viability of such a flow imposes on the central engines of bursts. v Acknowledgements This work was supported by a two year Fulbright grant and NSF grants AST 91-20599, AST 95-29170, AST 95-29175, and AST 98-76887. Contents Chapter 1 Introduction 1.1 1.2 1 AGNs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.1.1 AGN Classification . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.1.2 Accretion in AGNs and Unification of Radio Quiet AGNs . . . . . . . 5 1.1.3 Radio Loud AGNs . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.4 Relativistic Jets in AGNs . . . . . . . . . . . . . . . . . . . . . . . . . 10 GRBs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.2.1 Lightcurves and Timing . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.2.2 Spectra and Fluxes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.2.3 Afterglows . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 1.2.4 GRBs as Relativistic Flows . . . . . . . . . . . . . . . . . . . . . . . . 18 2 Jet Acceleration by Tangled Magnetic Fields 2.1 2.2 21 Tangled Fields as an Alternative . . . . . . . . . . . . . . . . . . . . . . . . . 21 2.1.1 The Twin Exhaust Model . . . . . . . . . . . . . . . . . . . . . . . . . 21 2.1.2 Compton Rockets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 2.1.3 Magneto-Centrifugal Acceleration . . . . . . . . . . . . . . . . . . . . 25 2.1.4 Tangled Fields . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 The Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 vii 2.3 2.4 2.5 2.2.1 Treatment of Magnetic Field . . . . . . . . . . . . . . . . . . . . . . . 30 2.2.2 Equations of Motion . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 Dynamical Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 2.3.1 Critical Points . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 2.3.2 The Effects of Gravity on the Sonic Transition . . . . . . . . . . . . . 40 Solutions in the Self-Similar Regime and Asymptotic Solutions . . . . . . . . . 44 2.4.1 Opening Angles and Causal Contact . . . . . . . . . . . . . . . . . . . 48 2.4.2 Equipartition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 2.4.3 Full Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 2.4.4 Radiation Drag . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 2.5.1 2.6 Tradeoff Between Dissipation and Acceleration and Synchrotron Brightness . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 2.5.2 Polarization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 2.5.3 Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60 Chapter Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 3 Energetics of Jets and the M87 Jet 3.1 66 The M87 Jet After 79 Years of Surveillance . . . . . . . . . . . . . . . . . . . 66 3.1.1 The Spectral Aging Problem . . . . . . . . . . . . . . . . . . . . . . . 70 3.1.2 Proposed Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 3.2 Adiabatic Effects on Synchrotron Emission . . . . . . . . . . . . . . . . . . . 75 3.3 Relativistic Effects . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 3.4 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 3.4.1 Confinement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 3.4.2 Comparison with Earlier Models . . . . . . . . . . . . . . . . . . . . . 92 3.4.3 X-ray Emission . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 viii 3.5 3.4.4 Polarization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 3.4.5 Particle Acceleration Radius . . . . . . . . . . . . . . . . . . . . . . . 97 Chapter Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 4 Evolutionary Signatures of Radio Galaxies 100 4.1 The Expansion of a Radio Galaxy: Connection Between CSOs and FRIIs . . . 101 4.2 Description of the Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 4.3 4.4 4.5 4.2.1 The Dynamical Model . . . . . . . . . . . . . . . . . . . . . . . . . . 102 4.2.2 Calculation of the X–Ray Brightness . . . . . . . . . . . . . . . . . . 106 4.2.3 Observational Diagnostics . . . . . . . . . . . . . . . . . . . . . . . . 107 Applications to Existing Data . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 4.3.1 Perseus A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 4.3.2 Other Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 Predictions for (Chandra) Observations . . . . . . . . . . . . . . . . . . . . . 115 4.4.1 Detectability of Young Sources . . . . . . . . . . . . . . . . . . . . . 115 4.4.2 Extended Sources . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119 4.5.1 Complications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119 4.5.2 Chapter Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 5 A Shotgun Model for Gamma-Ray Bursts 5.1 127 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 5.1.1 External Shocks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128 5.1.2 Internal Shocks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130 5.2 The Shotgun Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131 5.3 GRB Efficiencies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135 5.4 Simulating Lightcurves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 5.5 Afterglows in the Shotgun Model . . . . . . . . . . . . . . . . . . . . . . . . . 138 ix 5.6 5.7 Making Bullets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139 5.6.1 Why Bullets Must be Contained by Adiabatic Compression . . . . . . 141 5.6.2 Rayleigh-Taylor Driven Bullet Formation . . . . . . . . . . . . . . . . 143 5.6.3 Ram Pressure Confinement and Acceleration . . . . . . . . . . . . . . 145 Chapter Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153 6 Conclusions 154 Bibliography 159 Appendix A A More Realistic Dissipation Law for the Tangled Field Model 168 B Details of Synchrotron Emission 170 B.1 Synchrotron radiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170 B.1.1 Synchrotron Losses: . . . . . . . . . . . . . . . . . . . . . . . . . . . 170 B.1.2 Emitted Synchrotron Spectrum: . . . . . . . . . . . . . . . . . . . . . 171 B.1.3 Equipartition: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172 B.2 The Transport Equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173 B.3 Spectral Cutoff Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174 C Derivation of the Dispersion Relation for the Relativistic Rayleigh-Taylor Instability 176 Figures Figure 1.1 Approximate Composite Spectra for AGNs Compared to Normal Galaxies . . . 4 1.2 Cartoon of the Standard Accretion Picture in AGNs . . . . . . . . . . . . . . . 7 1.3 Image of Cyg A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.4 Cartoon of Cocoon-Shell Morphology . . . . . . . . . . . . . . . . . . . . . . 11 1.5 Lightcurves of a Sample of GRBs . . . . . . . . . . . . . . . . . . . . . . . . 20 2.1 Cartoon of Magneto-Centrifugal Acceleration . . . . . . . . . . . . . . . . . . 27 2.2 Cartoon of Tangled Field Model . . . . . . . . . . . . . . . . . . . . . . . . . 31 2.3 Solutions Around Critical Points . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.4 Map of Tangled Field Parameter Space . . . . . . . . . . . . . . . . . . . . . . 46 2.5 Acceleration Efficiency for Dissipative Jets . . . . . . . . . . . . . . . . . . 47 2.6 Equipartition for Dissipative Jet . . . . . . . . . . . . . . . . . . . . . . . . 50 2.7 Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 2.8 Radiative Efficiency of Dissipative Jets . . . . . . . . . . . . . . . . . . . . . . 55 2.9 Projected Brightness Profiles for Radiative Jets . . . . . . . . . . . . . . . . . 57 2.10 Projected Brightness Profiles for Non-Radiative Jets . . . . . . . . . . . . . . . 59 2.11 Synchrotron Polarization for Optically thin Jets . . . . . . . . . . . . . . . . . 61 3.1 Radio Image of Virgo A (Small Scale) . . . . . . . . . . . . . . . . . . . . . . 68 3.2 Optical and Radio Jet in M87 . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 xi 3.3 The M87 Jet Spectrum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 3.4 Emissivity Map . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 3.5 Cutoff-Frequency Fit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 3.6 Chi square–Contours . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 3.7 Best–Fit B-Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 3.8 Best–Fit vs. Equipartition Field . . . . . . . . . . . . . . . . . . . . . . . . . . 86 3.9 Estimated Errors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 3.10 Best–Fit Pressure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90 3.11 Best–Fit vs. Equipartition Pressure . . . . . . . . . . . . . . . . . . . . . . . . 91 3.12 Particle Acceleration Radius . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 4.1 Radial Density Profile for a Radio Galaxy Expanding Into a King Atmosphere . 109 4.2 ROSAT HRI Image of NGC 1275 (Perseus A) . . . . . . . . . . . . . . . . . . 111 4.3 Brightness Profiles for Slices shown in Figure 4.2 . . . . . . . . . . . . . . . . 112 4.4 Contours of Allowed Parameter Space for Figure 4.2 . . . . . . . . . . . . . . 114 4.5 Diagnostics for Small Sources . . . . . . . . . . . . . . . . . . . . . . . . . . 124 4.6 Detectability Constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125 4.7 Diagnostics for Large Sources . . . . . . . . . . . . . . . . . . . . . . . . . . 126 5.1 Illustration of the Angular Spreading Problem . . . . . . . . . . . . . . . . . . 130 5.2 Illustration of the Shotgun Model . . . . . . . . . . . . . . . . . . . . . . . . . 132 5.3 Constraints Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136 5.4 Real and Simulated Lightcurves . . . . . . . . . . . . . . . . . . . . . . . . . 138 5.5 Bullet masses from Rayleigh-Taylor Instability in GRBs . . . . . . . . . . . . 145 5.6 Cartoon of Ram Pressure Acceleration of Bullets . . . . . . . . . . . . . . . . 146 B.1 Theoretical Spectrum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175 Chapter 1 Introduction Astrophysical scenarios often offer unique settings to test and investigate extreme conditions which cannot be reproduced in a laboratory. An important class of objects fulfilling such a role are ultra-relativistic flows encountered in relativistic jets and gamma-ray bursts (GRBs). A thorough understanding of these flows will shed light on the complex astrophysical systems that they are part of, as well as enhance our understanding of the princ pal physical mechanisms behind the jet phenomenon. The conditions in these flows are extreme in two respects: first, they move at relativistic bulk speeds, with Lorentz factors1 of order Lorentz factors of order 10 in the case of AGN jets, and even higher 100 1000 in the case of GRBs. Second, the internal energy of these flows is dominated by relativistic forms of energy (rather than rest mass energy), at least in parts of the flow, like the injection region and the shocks found in knots and hot spots. This internal energy can be in the form of relativistic particle pressure, magnetic fields, or photons (or even neutrinos, as might be the case in GRBs). Whichever form of energy is chosen can have important consequences on the flow, as we will discuss in the following chapters. The result of these extreme conditions is an equally extreme display of power: AGNs continuously release amounts of energy that can outshine their host galaxies by orders of magnitude, and GRBs are so bright that they can briefly become the brightest objects in the universe, as they release the isotropic equivalent2 of more than a solar rest mass energy in only tens of 1 2 p is defined as 1= 1 v 2 =c2 , where v is the velocity of the object in question and c the speed of light. The isotropic luminosity is derived from the observed flux by assuming that the source radiates isotropically. If 2 seconds in gamma rays alone. This thesis will investigate several aspects of the relativistic flows that occur in radio galaxies and GRBs. Each chapter will contain a brief introduction to the specifics of the problem addressed in the chapter, while the remainder of this chapter will present a broader introduction of the field of AGNs and GRBs. The reader familiar with these topics can skip directly to x2. 1.1 AGNs Defining an AGN is not as simple as it may appear at first. While all AGNs have some outstanding characteristic, there is no one single observational marker that is shared by all types of AGNs (though some are very common). AGNs are best defined from a theoretical standpoint, since there exists a model that seems to apply to all types of AGNs: An Active Galactic Nucleus (AGN) is any galactic nucleus that harbors a massive accreting black hole. While this model has not yet been proven conclusively, we can use it as a working definition of AGNs for the time being, keeping in mind that, however unlikely, the theory might be wrong. The reasoning behind the black hole paradigm is indirect. Imaging black holes directly is one of the Holy Grails of astrophysics and many exotic proposals have been made for how to achieve this. The main difficulty is, of course, their small angular size: Even in M87 the event horizon of the hole has an angular size of only 2 micro arcseconds. The best resolution that can be achieved to date is roughly 100 times worse than that (Junor and Biretta 1995). We thus depend on circumstantial evidence. Luckily, such evidence has accumulated in recent years. The strongest arguments for the black hole paradigm include: Relativistic Iron K lines: Detections of extremely broad, double peaked lines with signatures of both gravitational redshifts and Doppler shifts corresponding to v > c=3 indicate the presence the radiation is beamed, the total energy released is reduced by the inverse of the covering fraction of the beam. 3 of strong gravity at work (Fabian et al. 1995). While the mass of the black hole cannot be determined by this method, the observations are inconsistent with any compact object other than a black hole, and are thus the best evidence for the existence of black holes yet. Water Masers: Water masers have been detected from several AGNs, where they occur in the outer (molecular) part of the accretion disk and can thus be resolved by VLBI. Very accurate redshift measurements can be used to map out the orbits of the material. The best candidates for this method are NGC 1068 and NGC 4258 (e.g., Kartje et al. 1999). Material has been observed to orbit in Keplerian motion around central masses of 3:5 107 M and > 107 M respectively, at radii of 0:13 pc and 0:65 pc respectively. The associated mass densities are difficult to explain with anything but a massive black hole. Variability: Causality constraints based on the observed strong variability on time scales of order days to years imply that the emission region must be no larger than the corresponding light crossing length. The enormous luminosities of AGNs suggest that, even with the most efficient mechanism known to release energy (per unit mass), millions to billions of solar masses are required to produce the energy emitted by some AGNs. The tight constraints on the size of the emitter, together with the mass requirements, strongly argue in favor of the black hole hypothesis (Rees 1978a). From the maser measurements and from the dynamics of the central stellar population, we know that the masses of these black holes range from 106 to 109 M . 1.1.1 AGN Classification In the following we will list the main observational characteristics of AGNs. Luminosity: Many AGNs emit at luminosities comparable to or surpassing the luminosity of their hosts. Estimates of AGN bolometric luminosities range from 1048 ergs s Lbol 1042 ergs s 1044 ergs s 1 . 1 , compared to the typical galaxy luminosity of L 1 to 4 1010 108 νFν 106 104 102 100 1010 1012 1014 ν 1016 1018 Figure 1.1: Composite spectra (Elvis et al. 1994) for radio loud AGNs (dotted line, stars), radio quiet AGNs (dash-dotted line, diamonds) compared to a dusty galaxy (dash-triple-dotted line, triangles) and an elliptical (dashed line, squares). Units are arbitrary Broad band continuum spectra: Most AGNs have very broad band spectra compared to normal galaxies, which feature spectra dominated by starlight (i.e., predominantly in the optical, or IR in the presence of dust). Most of the energy in normal galaxies is emitted over one or two decades in frequency. In contrast, most AGNs emit roughly equal amounts of energy over many decades in frequency, ranging from the IR, or even the radio in the case of radio galaxies, all the way to X-ray/gamma ray wavelengths. We can generally group AGNs into radio loud and radio quiet objects, with the obvious definition for both. To visualize the difference, Fig. 1.1 shows schematic composite spectra of the two classes. Variability: Since the light from normal galaxies is dominated by starlight, variability in normal galaxies is basically non-existent. On the other hand, AGNs can show variability on extremely short time scales: flux changes by a factor of two or more have been observed on time scales as short as hundreds of seconds at X-ray energies. At lower energies, the variability timescales tend to grow longer (months to years in the optical), and less pronounced. More luminous 5 AGNs tend to vary on longer time scales (consistent with larger black hole sizes). Very strong optical variability on time scales of days can be seen only in a few extreme classes of AGNs, namely blazars. Polarization: Most AGNs show slightly enhanced levels of polarization. In the optical, strong polarization in AGNs is generally associated with strong variability, while in principle every AGN that has resolved radio emission shows polarization at the few 10% level. Strong polarization generally indicates non-thermal emission mechanisms, most likely synchrotron emission (see Appendix B). Emission lines: Strong nebular lines characterize the spectra of most AGNs. These lines tend to be broader than those found in starburst galaxies, and in some classes of AGNs they can reach FWHM of 103 104 km s 1 . Even more extreme are the X-ray lines found in some Seyfert galaxies: they display FWHMs of c=3 and line shapes that can best be interpreted as relativistic distortions. Small angular sizes: Most of the IR/optical/X-ray emission is released very close to the horizon of the black hole, which makes it unresolvable with techniques available today. Apart from these characteristics, AGNs can share many more features. Given these commonalities among some AGNs, it has to be said that there is remarkable diversity among any random sample of AGNs. It is now believed that these differences can be resolved into a few basic groups of AGNs, coupled with orientation effects and changes in luminosity of their different components. 1.1.2 Accretion in AGNs and Unification of Radio Quiet AGNs The energy in AGNs is most likely released by matter falling down the potential well of the central black hole. This matter will carry angular momentum and thus cannot simply fall inward. Instead, the gas will settle into a disk. Viscous stresses (most likely due to magnetic 6 fields) will then slowly transport angular momentum outward, thus moving material inward. At the same time, orbital kinetic energy is released into internal energy. The disks tend to be the hottest closest to the black hole, which is why X-ray observations are the best candidates to probe the innermost regions of AGNs and the strong gravity of the central black hole. If a fraction of this energy is subsequently released in the form of isotropic radiation, we can place a fundamental upper limit on the luminosity and the associated accretion rate. If the radiative force on the flow exceeds the gravitational force, accretion is no longer possible. This limit is set by Ledd = 4GMmp c=T 1:3 1038 M=M ergs 1 ; (1.1) where M=M is the mass of the central object in units of solar masses, mp is the proton mass, c is the speed of light, and T is the Thomson cross section (e.g., Frank, King, and Raine 1990). The limit on the accretion rate then turns out to be M_ edd 4mp Rc=T : (1.2) Here, R is the radius of the central object. This Eddington luminosity is the natural value against which we much compare the emission from AGNs. This limit is independent of the geometry of the accretion disk. Several modes of accretion can occur, depending on the micro-physics, (most significantly, the cooling rate in the disk). If the disk can cool efficiently (i.e., most of the released energy is radiated) the disk will be relatively cold and geometrically thin. If instead most of the energy is trapped inside the disk (either due to opacity or radiative inefficiency), the disk is hotter and geometrically thick. The latter scenario has been dubbed “Advection Dominated Accretion Flow” (e.g., Narayan and Yi 1994), since most of the energy is advected through the horizon and never leaves the flow. Whether these ADAFs exist is still a topic of hot debate (e.g. Blandford and Begelman 1999). However, we are relatively certain that both radiatively efficient and inefficient flows do occur in AGNs. 7 τ >>1 Figure 1.2: Cartoon of the standard accretion picture in AGNs. Shown are the molecular torus (green) , the accretion disk (pink), the narrow line clouds (brown), the broad line clouds (yellow), a “corona” (red), the black hole, and an obscured and an un-obscured line of sight. Observations also suggest that at larger distances, where the angular momentum of the infalling matter is less severe of a constraint, matter can form a toroidal structure. At those distances, the temperatures in the accreted matter are sufficiently low for most of the material to be molecular and dusty. Figure 1.2 illustrates the general picture. Radio quiet AGNs can be explained on the basis of this picture alone: Broad emission lines are produced by clouds orbiting relatively close in (the broad line region), while narrow lines are produced farther out, where densities are lower (thus we can see both forbidden as well as permitted lines). The torus can obscure the central source (and the broad line region) and, at the same time, scatter some of the light back into the observer’s line of sight. The orientation of the observer with respect to the axis of the torus therefore determines what is seen by the observer (Antonucci and Miller 1985). In this picture, Seyfert 1s are seen more face on, while Seyfert 2s are seen edge on. The luminosity of a typical AGN will roughly scale with the mass of the central black hole (equation 1.1). Together, orientation and luminosity can account for most of the variation seen in radio quiet AGNs. 8 1.1.3 Radio Loud AGNs About 10% of all AGNs show enhanced radio emission (see Fig. 1.1), at about a tenth of a percent of the bolometric luminosity of the source. The radio emission generally exhibits high linear polarization, indicative of its synchrotron origin. Furthermore, in many cases the radio emission can be spatially resolved, unlike the rest of the AGN spectrum. Thus the radio brightness must be due to a separate mechanism from the nuclear emission. In general, radio loud AGNs are referred to as radio galaxies (radio loud quasars are often classified separately as radio quasars). We can divide the class of radio loud AGNs according to their brightness distribution: sources that emit most of their radio power on larger scales (kpc, well resolved) are called lobedominated sources, and those that emit on small scales (pc scales, mostly unresolved with VLA) are called compact or core-dominated objects. In the lobe-dominated class, the morphology of the resolved structure shows three distinct components: On the largest scales we see diffuse emission from two oblong regions on opposite sides of the nucleus, roughly in the shape of balloons. These structures are called the radio lobes (thus the classification of the sources as lobe-dominated) and can be hundreds of kiloparsec in size, larger even than their host galaxies. The nucleus itself can generally also be seen. Finally, connecting nucleus and lobes are two narrow beams of radio emission, which, though not visible in all cases, are generally believed to exist in all sources, as they are thought to feed the lobes. These beams are called the radio jets and their properties shall occupy most of this thesis. Figure 1.3 shows some examples of radio galaxies. Both jets and lobes show significant amounts of linear polarization. The morphology and radio power of radio galaxies are generally correlated. Low power sources with radio power below Lrad 1042 ergs s 1 show rather curvy jets on both sides of the nucleus. Their radio lobes tend to be brightest closest to the nucleus and fade towards their edges (which are consequently not very well defined). Radio Galaxies falling into this category 9 Figure 1.3: VLA map of prototypical FR 2 radio galaxy Cyg A. are classified as FR 1 sources (Fanaroff and Riley 1974). Members of the more powerful FR 2 class, with radio power in excess of Lrad 1042 ergs s 1 , tend to show a straight jet on one side of the nucleus only, while the lobes are edge-brightened and well defined, showing very bright “hot spots” at the end of the jet-lobe structure. The cores of both core- and lobe-dominated sources show elongated structure when resolved with VLBI. The radio spectra of these sources generally exhibit power-law behavior with fluxes obeying the relation F / . For the lobe-dominated sources, the power-law indices fall into the range from 0.5 to 1, while compact sources tend to be flatter, with 0. Together with the polarization information, the spectra point towards synchrotron radiation as the mechanism for the radio emission (see Appendix B for a brief review). The flatness of compact sources can be understood as a superposition of self-absorbed spectra. In these sources, we can also see significant contribution of synchrotron radiation at IR and even optical/UV wavelengths, sometimes overpowering the thermal emission and line emission from the “ordinary” AGN. These sources also show polarization and strong variability in the optical band and are referred to as blazars. In these sources, it is believed that relativistic effects enhance the jet emission so much that it 10 dominates the overall appearance of the source. Among the compact sources, the Compact Steep Spectrum sources (CSS sources Fanti et al. 1990) and Gigahertz Peaked Sources (GPS sources O’Dea et al. 1991) show distinctly nonflat spectra. Resolved images expose them to be intrinsically small radio galaxies. A related class of sources are the compact symmetric objects (CSOs, smaller than 500 pc, Wilkinson et al. 1994) and medium symmetric objects (MSOs, 0.5 to 15 kpc, Fanti et al. 1995), which show a symmetric but miniature jet-lobe structure. 1.1.4 Relativistic Jets in AGNs Jets are at the heart of radio loudness in AGNs. They are very fast collimated outflows of highly energetic plasma. The projected opening angle of AGN jets is often only a few degrees and they can be very straight (see, for example, the image of Cyg A in Fig. 1.3). The jets are collimated and collinear over several orders of magnitude in length and often show clear signs of elongation on the smallest angular scales resolved (e.g., NGC 6251 Perley et al. 1984). The surface brightness of radio jets tends to be concentrated into (often relatively evenlyspaced) smaller knots rather than having smooth surface brightness distribution. Far downstream the originally straight jets often become more curvy (possibly due to their decreasing speed and interaction with ambient material - called the “dentist drill” effect, Scheuer 1982) and terminate in the hot spots of the lobes. This suggests that the lobes are fed with relativistic plasma by the jets. Both analytic models and numerical simulations show that the interaction of the head of the jet with the ambient material results in a strong shock and a backflow of material, which forms a cocoon-like structure around the jet, called the radio lobes. This picture, outlined in Fig.1.4, will be built on in x4 to develop a powerful method of analyzing X-ray images of radio galaxies. Some jets are also visible at optical and UV frequencies, and several jets have even been detected in soft X-ray, most notably M87 (Biretta et al. 1991), 3C273, and most recently PKS 0637-752 (Chartas et al. 2000). As with the lobes, we know that the radio emission from the jets is of synchrotron origin. The same is true for the rest of the spectrum 11 shell expansion n coconosion expa back flo w AGN "dentist drill" jet hot spot shocked ISM shell cocoon (relativistic plasma) contact discontinuity Figure 1.4: Cartoon of the morphology of an intact radio galaxy. The radio plasma in the cocoon is shown in blue, the IGM, which follows a King profile, is shown in pink, the shocked shell in red, and the jet in green. The arrows indicate motion (not to scale). According to the “dentist drill” effect, the jet is shown to wiggle, causing the effective area of the hot spot (the termination shock of the jet) to be much larger than the area of the jet. with the possible exception of the X-ray emission, which could also be due to inverse Compton scattering. As is true for radio lobes, radio jets often show a significant amount of polarization, reaching levels of a few tens of percent (compared to the maximum of 70% for typical radio spectral indices 0:5). While this indicates the presence of magnetic fields, it does not imply that this field is well ordered over large scales (see x2). The field orientation can be parallel or perpendicular to the direction of the jet and can change abruptly, as can be seen, for example, in the knots of M87. Proper motion measurements of the knots sometimes show apparent velocities in excess 12 of the speed of light. Superluminal motion is caused by the apparent retardation of light emitted by the moving object; a radiation source moving at a small angle towards the observer at close to the speed of light will show an apparent motion app the sky (Rees 1966). The inferred actual vapp =c faster than 1 on the plane of of the emission region (which can either be a bulk velocity of an emitting plasma blob or a pattern speed of a bright region in the flow, as would be encountered in a shock) must be comparable or larger than app , while the viewing angle must be smaller than, or comparable to 1=app . A stronger argument for relativistic bulk motion in jets is the fact that we often only see one jet where there are two radio lobes and the two associated hot-spots. Clearly, if the idea of hot spots and lobes being created and fed by the jets is correct, a second jet should be present yet hidden from our view. This is exactly what we would expect if the bulk speed of the jet plasma were relativistic and if the angle between the approaching jet and the line of sight were small. This effect is due to relativistic beaming and will be extensively referred to in x3. A third argument for relativistic motion is the strong variability seen in blazars. As with GRBs, the only reasonable explanation for the fast variability combined with such large fluxes is relativistic bulk motion. While the above arguments only supply approximate lower limits to , the most plausible range of Lorentz factors compiled from all these arguments falls in the range we adopt a fiducial value of 10. 3< < 100; For a jet to be visible at all at such large , it has to be pointing roughly in our direction, which immediately introduces a strong angular dependence of the observational signatures of the jet. Coupled with variations in the kinetic power and emissivity in the jet, we can explain the differences in FR 1 and FR 2 as due to FR 2s having consistently larger radio power, while blazars and BL Lacs are oriented so closely towards the observer that relativistic beaming affects the whole spectrum, swamping out emission lines and introducing variability and polarization even at optical frequencies. While it is now widely accepted that jets move at relativistic bulk speeds, the physical conditions inside the jet are far less well known. Estimates of magnetic field strength and 13 particle pressure depend on the assumption of equipartition between the two. While providing us with an estimate that is probably accurate to within an order of magnitude, it does not resolve the question which form of pressure dominates the internal energetics of the source. This very important question in terms of jet dynamics and jet emission will be discussed in x2 and x3 respectively. Furthermore, the composition of the jet plasma is unknown: it can be made up of either pairs or of electrons and ions. The nature of the particles also has important consequences for jet dynamics, since the baryon density in the jet will determine the terminal Lorentz factor that can be achieved in the acceleration phase. Both of these issues can in principle be resolved with high resolution broadband imaging. Finally, the most pressing open issue is the question of jet production and dynamics. A number of promising models have been proposed, which we will briefly mention here and describe in more detail in x2. There are a number of channels other than radiation through which the accretion energy can be released. Most notably, both Poynting flux and simple kinetic energy flux (in the form of a wind) can remove energy from the flow. If the luminosity in these channels is comparable with the Ledd , we can expect to see a dramatic effect on the overall structure of the flow. The amount of energy available could easily explain the energy released in jets. The ubiquitous presence of accretion disks in astrophysics and the abundance of energy released by them strongly points towards black-hole-accretion disk systems as the origins of AGN jets, especially since we can see the signatures of both jets and disks in some cases. For the rest of this thesis we shall assume that jets are produced in the inner regions of the accretion disk/black hole system. Any jet model must explain two things: the acceleration of the plasma to Lorentz factors of order 10, and the collimation of that flow to narrow opening angles. Acceleration can be provided by several means: Internal energy of relativistic particles (BR74). In this case, the terminal Lorentz factor of the 14 flow is given by the average random particle Lorentz factor at the base of the flow, modulo losses of energy through other channels like radiation. Collimation must be provided by an external agent, such as static pressure in the surrounding medium. Inverse Compton enhanced radiation pressure (O’Dell 1981). This mechanism is based on the fact that a region containing relativistic particles in the presence of a strongly anisotropic radiation source will be accelerated away from that source, which also provides the collimation. Poynting flux in large scale organized fields (Blandford and Payne 1982). This is the standard model for jet production. Acceleration is provided by centrifugal forces along inclined field lines, electric fields induced by rotation of the field in the rotating frame of the accretion disk or a spinning Kerr black hole, and simple pressure gradients of particle and field pressure. Collimation is provided by tension in the toroidal field and stresses communicated along the jet from the inner disk. All of these models have shortcomings and, while the latter model has been embraced by most researchers in the field, it has not been proven conclusively. In x2 we will outline where these models run into difficulty and we will offer a complementary approach to the organized field model. 1.2 GRBs While we do not have any direct observations of jets in Gamma Ray Bursts (GRBs), there is now increasing evidence that they too exhibit collimated relativistic outflows (e.g. Stanek et al. 1999). The physics behind GRBs is even less clear than in the case of AGN jets, thus we are limited to very crude models and collimation of the flow is mostly treated as an afterthought. GRBs were discovered in the 1960s by a system of satellites monitoring circum-terrestrial space for nuclear explosions, which had been banned by the “Outer Space Treaty”. It was soon discovered that they were extra-terrestrial in origin, and rather mysterious in nature. Since 15 their discovery we have learned a good deal about their origin, yet a large part of their mystery remains. A GRB is a very bright flash in gamma rays that lasts anywhere from less than one second to a few hundred seconds. BATSE, the most prolific GRB monitor, detected about one burst per day, with high sensitivity and almost perfect sky coverage. This number has to be compared to the estimated rate of supernovae in the entire universe of about 1s 1 (the reason will become apparent when we discuss GRB progenitors). GRB light curves show variation on time scales as short as 1 millisecond and for the time they emit, they can outshine the entire gamma ray sky. Their positions are distributed isotropically, which implies that they must originate either in the outer solar system, the halo of the Milky Way, or on cosmological scales. Until the discovery of GRB afterglows in galaxies at cosmological redshifts, the distance scale of GRBs was an open question, and for short duration GRBs, for which there have not been any afterglow detections, it still is unknown. 1.2.1 Lightcurves and Timing Figure 1.5 shows light curves from a small sample of GRBs. Above all, they show the intrinsic diversity in GRBs: light curves can be smooth and single humped or very spiky, with no apparent pattern in the peaks. Upon closer investigation, the envelopes of many bursts do show a commonality: they seem to follow a fast-rise exponential-decay (FRED) profile (seen, for example, in burst 971208 in Fig. 1.5). Zooming in on the individual spikes reveals that they also appear to follow a FRED profile. FREDs are not uncommon and can be produced by a number of processes, which has led to literally hundreds of proposed models for GRBs, most of which can be classified as rather unorthodox (or even perverse, Rees, private communication). GRBs are detected by all-sky gamma ray monitors that have built-in triggers. They continuously monitor the gamma-ray sky and whenever a significant rise in flux over the background is observed, they send an envelope of data bracketing the trigger event to the ground. 16 The positional information can be used by other instruments to look for signals in other wavelengths from the GRB, or simply to improve the accuracy of the GRB position with follow-up observations. GRB durations are often measured in cumulative fluxes: t50 is the time between the points where 25% and 75% of the total flux have been received, while t90 is the time between the points when 5% and 95% of the flux have been received. Grouping GRBs by their duration reveals a clearly bimodal distribution. GRBs fall into two categories: short duration bursts, which last less than about a second, and long duration bursts, which last longer than roughly 1 second. Due to their brief existence, it has been impossible to observe signals from short duration bursts at longer wavelengths. As a result, we have very limited information about their nature. Most research has thus been concentrating on long duration bursts, and for the rest of the thesis we too shall only be concerned with long duration bursts. That is not to say that the theory presented cannot be applicable to short duration bursts as well, but the existing observational body is too small to support or rule out any such statement. The power spectrum of a large sample of long duration bursts has been studied by Beloborodov et al. (1998). It shows a rise at low frequencies corresponding to the distribution of burst durations, a portion that follows a power law with slope 5=3, and a steep drop of on time scales shortward of 1 Hz. The power-law part of the PSD is indicative of the distribution of individual spikes and should included in any GRB theory. 1.2.2 Spectra and Fluxes The only spectral information we have about GRBs is from the gamma rays, with one exception, GRB990123, which was simultaneously detected in the optical, but only in one filter. Within the limits of the spectral window of BATSE (sensitive from about 20 keV to 600 keV) and OSSE, which observed some bursts simultaneously with BATSE, GRBs show a broad, nonthermal spectrum that typically peaks at around 200 keV. While the flux drops off to both sides 17 of the peak, F can be almost constant at the high energy end of the spectrum, while the one optical point available lies far below the gamma rays, indicating that F drop off quickly at lower energies. Keeping in mind that the spectral shape above the peak is somewhat uncertain and that a significant amount of energy might be hidden at unobservably high energies, the fluence of the GRB can be estimated by F;peak . If afterglow observations (see next paragraph) provide the distance to a given burst, the isotropic energy it radiated can be calculated by multiplying the fluence with 4d2 , where d contains the necessary cosmological corrections. The inherent assumption in calculating this value is that the burst radiated isotropically, which, while convenient, might well be wrong. For the O(30) GRBs for which redshifts have been obtained, the inferred isotropic energies are staggering: within only a few tens of seconds GRBs can release anywhere from few 1054 ergs s 1051 to 1 , more than a solar rest mass, in gamma rays. Coupled with their fast variability, this places severe constraints on the physics of GRBs (see 1.2.4). 1.2.3 Afterglows The launch of Beppo-SAX, with an onboard burst monitor and a high resolution X-ray imager, led to the discovery of emission from GRBs at other wavelengths. This is accomplished by imaging the location of the burst at high enough X-ray spatial resolution that the location of the fading X-ray source that is sometimes associated with the GRB can be determined. The X-ray emission is generally detected after the GRB is over and is qualitatively different from the GRB in that it does not show rapid variability. Any emission that is discovered after the GRB itself has ended is called afterglow. With accurate positions, other instruments can look for emission from the GRB successor and indeed, afterglows have been found at optical and radio wavelengths. Optical images reveal that GRBs are generally associated with galaxies, and redshift information from these galaxies shows them to lie at cosmological distances. Afterglows generally exhibit powerlaw spectra that can be explained by synchrotron 18 emission that is self-absorbed at low energies and shows a cooling break that moves to lower energies as the afterglow ages. In some bursts, the afterglow seems to show additional breaks late into its evolution. As the peak of the emission moves to lower energies with increasing age of the afterglow, the brightness slowly fades, also following a powerlaw behavior. 1.2.4 GRBs as Relativistic Flows The fact that GRBs are so bright and at the same time release most of their energy in gamma rays within a few tens of seconds puts severe constraints on their physical nature. If GRBs were non-relativistic, the standard causality argument (used above as an argument in favor of black holes present in AGNs) would limit their typical size scales to only few 1011 cm. The fast variability on time scales as short as a few milliseconds reduces these limits by another few orders of magnitude. The presence of gamma rays implies that photon-photon interactions will lead to copious pair production. The compactness parameter, which measures the importance of photon-photon interactions, greatly exceeds unity for a non-relativistic GRB: l 108 . As a result, pair production would quickly raise the optical depth in GRBs to LTE values (many orders of magnitude larger than unity), which would render the bursts completely opaque, making the escaping spectrum thermal (in contradiction to the observed non-thermal gamma ray spectrum) and prolonging the burst duration to lengths inconsistent with the observations. The solution to this dilemma is the same that has been found to work in blazars: relativistic bulk motion with 1 can explain the fast variability and the non-thermal GRB spectrum without running into difficulty with the extreme luminosity of the burst. This is because the observed variability time and burst duration in a relativistic flow are shorter than the corresponding comoving time scales by a factor of order 1= 2 . This is due to retardation of the radiation emitted in the comoving frame, which shortens the observed emission time scale obs by a factor of order 1= 3 , and time dilation, which stretches obs by a factor of . The implied size of the emission region is correspondingly larger. In addition, a Doppler shift in the observed frequency implies that the average photon energy in the comoving frame is lower by a 19 factor of order 1= , reducing the number of photons able to pair-produce by a factor / 1= 2 , where need is the spectral index defined above. In order to avoid the compactness problem, we > 100, larger than typical AGN jet Lorentz factors by an order of magnitude or more. This makes GRBs the most extreme large scale test-beds for special relativity known to date. The question then arises as to what causes the gamma-ray emission. If the energy radiated away in the GRB were simply carried along as internal energy, the ratio of kinetic to radiated energy would be large and the efficiency of the burst would in turn be very low. The energy requirements for such a burst would be staggering. It is thus most commonly assumed that the internal energy in the burst is recovered from the kinetic energy in the flow by shocks slowing the material down to only “moderately” relativistic speeds (i.e., 10, roughly corresponding to braking from ludicrous to ridiculous speed, Brooks 1987). The cause of these shocks is the defining feature for the two mainstream GRB models. In the external shock model, interaction with the external ISM leads to a strong shock that produces the gamma rays, whereas in the internal shock model the flow shocks with itself due to variation in the outflow speed of the material. These two models will be outlined in more detail in x5.1. 20 250 GRB980923 14000 GRB980425 GRB990123 4000 200 12000 150 3000 8000 100 2000 6000 50 10000 1000 4000 2000 0 0 10 20 30 40 50 60 0 20 40 60 80 0 0 50 100 150 500 2000 GRB971209 GRB971214 GRB980124 3000 400 2500 1500 300 1000 200 500 100 2000 1500 1000 500 0 0 0 2 4 6 8 10 12 0 20 40 60 80 1500 1400 0 0 20 40 60 80 100 500 GRB910711 GRB970925 1200 GRB971208 400 1000 1000 300 800 600 200 500 400 100 200 0 0 0 0 2 4 6 8 10 12 0 20 40 60 80 0 200 400 600 800 Figure 1.5: Archival lightcurves for a sample of GRBs as seen by BATSE. Vertical axis: counts/sec in all four channels; horizontal axis: time in seconds. Note that the change in the variability/noise level in GRB971208 at 600 sec is due to a change in the binning factor. Remarkable bursts in this sample are GRB990123: the most energetic burst seen and the only burst for which a contemporaneous optical counterpart has been detected; GRB910711: the the burst with the shortest time scale variation ever observed ( 3ms); GRB971208: the longest and smoothest burst ever observed. Chapter 2 Jet Acceleration by Tangled Magnetic Fields 2.1 Tangled Fields as an Alternative The key unsolved issue in jet physics is the question of jet creation. In other words: what mechanism provides the large amounts of energy-momentum flux we see in relativistic jets and at the same time restricts this flow to an opening angle of < 10Æ ? We know from independent arguments that black holes can most likely be found at the centers of both AGNs and GRBs (all serious GRB engine models ultimately form a black hole at their center). We also know that the most efficient and readily available way of energy release for ordinary matter is conversion of gravitational energy into other forms of energy when falling down the gravitational potential of a compact object. This mechanism is well known to operate both in Galactic compact objects (specifically, X-ray binaries) and AGNs. The introduction mentioned the three most probable models for jet acceleration, which we will investigate now in a little more detail. 2.1.1 The Twin Exhaust Model The first model that is a viable candidate for the large-scale dynamics of extragalactic radio jets is the ‘twin exhaust’ model (Blandford and Rees 1974, BR74 throughout the rest of this thesis). In this model, ordinary relativistic particle pressure provides the bulk acceleration via conversion of internal to kinetic energy, i.e., simple adiabatic expansion. On a superficial level, this model corresponds to the standard polytropic solar wind model. The underlying assumption in this model is that the pressure of the external medium 22 surrounding the jet is stratified. This is not an unreasonable assumption, since the central black hole as well as the host galaxy and (if the AGN is located in a cluster) the cluster provide a strong gravitational potential in which any quasi-static medium would necessarily develop a strong pressure gradient. An even steeper pressure gradient could be expected if the medium were not stationary but in the form of a slow (i.e., non-relativistic) wind. In any case, we can expect the pressure of the ISM/IGM to decrease with distance from the center. Since the wall in a stationary jet does not expand sideways, the jet must be in pressure equilibrium with its surroundings. Since the external pressure is stratified, the jet will also be stratified, and if the jet is non-radiative, it will expand adiabatically to satisfy this requirement. Since the symmetry of this problem is broken by the geometry of the accretion disk, we can expect most of the energy released in the central region to escape preferentially along the symmetry axis. The equations of motion then dictate that the flow accelerate along that axis and that its cross section contract for the sub-sonic portion of the flow and expand for the supersonic portion. In other words, the flow goes through a self-imposed De Laval Nozzle. In the ultra-relativistic part of the flow (i.e., where jet (r ) Rjet (r) where r / pext (r) / 1) we simply have (see BR74): 1=4 jet ; (2.1) is the distance from the center, pext is the external pressure, and the jet. The jet is collimated as long as d2 R=dr 2 Rjet the radius of < 0, i.e., as long as d ln pext =d ln r < 4, a reasonable assumption. This does not guarantee that the flow will stay in causal contact with itself and its environment, however. That question will be addressed in x2.4.1. It has to be noted that the acceleration in this model is rather gradual, since the Lorentz factor only varies as the 1=4 power of the external pressure. Since the relativistic core of the flow must be injected close to the horizon of the black hole (say at 10 gravitational radii), there are many decades in radius to provide enough acceleration to get up to Lorentz factors of order 10 and higher. There are, however, more serious problems this model must face up to: 23 First, cooling processes for particles with highly relativistic random motions (necessary to produce outflows with large bulk Lorentz factors ) are very efficient (both synchrotron and inverse-Compton cooling go as 2 ). These loss processes compete with and possibly disable bulk acceleration. Second, the external pressure required to contain the flow must be equal to the internal pressure of the jet. For standard ISM/IGM densities, this would imply higher pressures than observed by X-ray observations of AGN environments. This problem could be circumvented by a slow wind surrounding the relativistic core of the jet; Compton drag can also hamper the efficiency of this process since a significant fraction of the particles are relativistic (see x2.4.4 below). 2.1.2 Compton Rockets Since relativistic jets are known to contain ultra-relativistic particles (i.e., particles with relativistic random motions), Compton scattering off of those particles must be very efficient. Compton up-scattering is isotropic in the frame of the relativistic particle as long as the photon energy in that frame is small compared to the particle rest mass. If the relativistic particle encounters a photon, it will preferentially be scattered away from that photon, because the energy and momentum transfer from electron to photon peaks for head-on collisions, and even though the photon direction in the particle frame will be beamed towards the direction of motion of the particle, statistically, the angle of incidence in the observer’s frame will lead to a stronger momentum transfer for head-on scattering. Thus, a cloud of ultra-relativistic particles in the presence of a highly non-isotropic radiation source (the best example here would, of course, be a point source) will accelerate away from that source very quickly. The accelerative force on the cloud will be proportional to h 2 i=h i, since the energy transfer by inverse-Compton scattering for a particle goes as 2 while the inertia of the particle is proportional to . This process was originally proposed as a mechanism for jet acceleration by O’Dell (1981) and has been dubbed the “Compton Rocket”. 24 While this mechanism does not in itself provide a means of collimation, the fact that matter will be propelled radially away from the radiation source can lead to jet formation if the symmetry of the system is broken. In particular, a geometrically thick accretion disk can funnel and shield the flow. In such a model, relativistic plasma is released in the evacuated funnel along the rotation axis, with most of the radiation intercepted by the accelerated plasma coming from the center of the funnel. However, very soon after the Compton rocket was proposed, it was realized that the same process that causes this strong acceleration also puts severe limits on the efficiency of the Compton Rocket. Radiative losses in this scenario will limit the terminal bulk Lorentz factor of the flow to 1 3 (Phinney 1982, which also provides a sound derivation of IC acceleration). One could imagine a scenario where relativistic particles in the jet are constantly replenished (an assumption also employed in other contexts, see x3.2, also x2.2.1.2). There is, however, an even more severe problem: The radiation field encountered by the jet, while likely anisotropic, is not going to correspond to a pure point source. As soon as the jet reaches a bulk Lorentz factor large enough to make the radiation field in the rest frame of the plasma isotropic by relativistic aberration, the acceleration will terminate and the jet will simply cool radiatively. In other words, the Lorentz factor is limited by the opening angle O of the radiation source, 1=O. In fact, radiation drag can actually decelerate the jet if the external radiation field is isotropic in the lab frame, which leads to both random energy losses and kinetic energy losses by the same process. Nonetheless, it is worth investigating the effects of radiation drag in jet physics and research on radiative acceleration is currently being pursued by several groups. Some recent publications in the field include Renaud and Henri (1998); Sikora et al. (1996); Luo and Protheroe (1999) and references therein. 25 2.1.3 Magneto-Centrifugal Acceleration The most widely accepted model for jet acceleration is magneto-centrifugal acceleration, as proposed by Blandford and Payne (1982). Acceleration and collimation are provided by organized magnetic fields and since the energy is initially stored in the field, radiative losses are much less limiting in this model. Except for the Blandford-Znajek effect (which will be discussed below) all of the flavors of this model derive the energy that drives the flow directly from the orbital energy of the accretion disk. The particle densities and ionization fraction in the disk will likely be high enough to justify the magneto-hydrodynamic approximation and thus any magnetic field present in the disk will be frozen into the plasma by virtue of the induction equation. If a large scale poloidal field (any field perpendicular to the toroidal, i.e. component of the field) is present, it will be dragged along by the orbital motion of the plasma. This will wind up the field (i.e., introduce a toroidal component) and it will also act as a slingshot: a blob of plasma sitting above the disk (e.g., in a corona) will be accelerated along the field line it is sitting on by the centrifugal force due to the rotation of that field line as long as the angle between the field line and the disk surface is less than 60Æ and the field points away from the disk center. Once the outflow is launched by this slingshot mechanism, tension in the field will collimate the flow (two effects contribute here: tension due to the toroidal component as well as tension in the poloidal component that is communicated downstream from the disk, where the field lines are anchored and cannot move outward). Gradients in the magnetic and particle pressure will also act to accelerate the flow. Figure 2.1 demonstrates the different ingredients of this picture. Depending on the uniformity of the field, the wound up field lines imply that a current must flow along the jet due to Ampere’s law. In order to conserve charge, this current must return to the disk/black hole. In order to close the current loop, the assumption of zero resistivity must break down somewhere downstream. While this is a good assumption, the details of this process are critical to determining the actual power of the jet. Since we have no good 26 understanding of this aspect of the flow, a critical piece of the puzzle is still missing even if the jet is accelerated by these MHD effects. Many different modifications of this model have been investigated in a large body of research, a cross section of which can be found in Blandford and Payne (1982); Heyvaerts and Norman (1989); Li et al. (1992); Camenzind (1986); Okamoto (1979) and references therein (the latter three references deal with the relativistic complications encountered in real jets). The magneto-centrifugal model has a number of advantages over the previous two approaches. As mentioned, radiative losses are not as important. Furthermore, we know from observations that jets do contain magnetic fields. How much energy is present in those fields is an open question (see x3), but even if the field is below equipartition (as defined in xB.1.3), it is lower by only an order of magnitude or so. Finally, the model provides a simple explanation for both acceleration and collimation by the same process, which means less stubble for Ockham’s razor. There are, however, a number of shortcomings. First, it is not at all clear if a large scale ordered field can be maintained above a disk. Such a field would either have to be dragged in with the accreted matter, or it would have to be generated in the disk via dynamo-processes. If the accretion is based on angular momentum transport via magneto-turbulent viscosity, it is unlikely that the disk can drag in sufficient poloidal flux to support a jet, as has been argued by Lubow, Papaloizou, and Pringle (1994a). If instead angular momentum transport occurs via a disk wind, it might be possible to support the proper field geometry simply by field dragging, however, such disks seem to be unstable (Lubow, Papaloizou, and Pringle 1994b). This leaves field generation by a disk dynamo, as has been investigated in a first attempt by Tout and Pringle (1996). In this case, turbulence in the disk due to magneto-rotational instabilities (MRI Balbus and Hawley 1991) produces a predominantly toroidal field, although it might be possible to generate poloidal field along the way via a turbulent cascade. This question has yet to be properly investigated, preferentially with the help of high-resolution numerical simulations. Any force transfer through the magnetic field, which ultimately helps to collimate and 27 wou nd-u p fie magnetic pressure gradient ld magnetic tension b blo cence ac plas ma tri ler fuga a ti l on Disk rotation Figure 2.1: Cartoon of the general mechanism in magneto-centrifugal acceleration. Plasma is flung out along field lines anchored in the accretion disk. For this to work the angle between disk and the field line must be 60Æ . The flow is collimated by magnetic tension. Further acceleration is provided by pressure gradients in the wound-up field and in particle pressure. accelerate the jet, can only occur within the Alfven surface (the surface where the fluid becomes super-Alfvenic). Beyond this surface, the fluid is causally disconnected from the disk and will essentially act as a free fluid and it is therefore likely that another form of collimation would have to come into play (i.e., external pressure confinement, Begelman 1995, B95 hereafter). 28 Furthermore, the rate of acceleration is rather slow, roughly logarithmic, which would make it difficult to convert a large fraction of the Poynting flux into kinetic energy flux (Begelman and Li 1994). Finally, magnetically collimated flows are violently unstable to pinch and kink instabilities (Begelman 1998; Eichler 1993). Any such flow will be disrupted quickly and depart from any self-similar structure it might have had, and thus from the analytic solutions found in the above-mentioned publications. If collimation of jets by ordered fields is possible, it must look somewhat different from any of these approaches. The Blandford-Znajek Mechanism (Blandford and Znajek 1977) is, in a sense, a subcategory of magneto-centrifugal mechanisms. The energy flux in this picture is provided by conversion of the spin-energy of a Kerr black hole into Poynting flux. For this mechanism to work, a sufficient amount of magnetic field must thread the horizon of the black hole, which acts as a fly wheel that drags the magnetic field along due to its finite resistivity. If this assumption is satisfied, a very large energy reservoir can be tapped into to power the jet at rapid rates. Collimation must be provided by the usual means (either magnetic self-collimation or external pressure). Recently a vigorous debate has arisen regarding the viability of producing sufficient field strength in the vicinity of the black hole (Livio et al. 1999; Krolik 1999). 2.1.4 Tangled Fields Polarization measurements show that the magnetic field in jets is probably not well or- ganized — the polarization is generally well below the maximal value of 70%; only in knots does the polarization tend towards this value (note, however, that interpretations of polarization measurements are often ambiguous, since different field geometries can sometimes lead to the same net polarization). This argues for the presence of largely unorganized, chaotic fields, which could easily account for the high polarization measured in the knots if they are interpreted as shocks, compressing the field in the shock plane (Laing 1980, B95). This goes hand in hand with the fact that the field produced in the disk by dynamo processes is expected to 29 be highly chaotic. Since the conditions in the jet will likely be controlled by disk physics, we should expect the same statement to be true for the magnetic field in the jet at least close to the disk. These arguments led us to investigate the dynamics of jets containing large amounts of such disorganized magnetic fields. The rate of acceleration in a jet propelled by internal (isotropic) particle pressure in an external pressure gradient is limited to to bulk Lorentz factors of / pext 1=4 (BR74), which means that the acceleration 10 100 would occur over length scales > (1000) rg for external pressure gradients p / z 2 . One might think that an anisotropic pressure in the form of chaotic magnetic fields could increase the rate at which the jet is accelerated, if the excess momentum flux is oriented along the direction of the jet. However, we will show that under a given set of simple assumptions the rate of acceleration is actually the same as in the classic case considered by BR74, i.e., / pext 1=4 . It is unlikely that the magnetic field evolves without some form of dissipation, especially if it is highly unorganized (reconnection is a diffusive process, so strong gradients in the field, as are present if the field is highly tangled on small scales, will likely lead to increased dissipation). These loss processes can compete with the efficiency of bulk acceleration by removing energy from the flow reservoir. We will investigate the effects that such a tradeoff might have on the dynamics and appearance of jets. 2.2 The Model The model we are employing here is closely related to (and an extension of) the ‘twin- exhaust’. We adopt a similar scenario under which the jet is launched into a stratified external medium. In the case we are considering, turbulent and highly disordered magnetic fields dominate the internal energetics of the jet. See also Heinz and Begelman (2000). We have illustrated the overall picture of the model in Fig. 2.2: Interstellar magnetic field is advected inward by the accretion disk. Turbulent shear then amplifies the field and tangles it up (dynamo action). This effect will grow stronger with decreasing distance to the black hole. 30 Eventually, regions of very high field strength will develop. Due to their buoyancy they will accelerate away from the black hole, forming an initial outflow. This outflow is then collimated by the pressure of the external medium. The jet channel is constrained by pressure balance, i.e., the jet will expand or contract in such a way that an equilibrium solution is set up for which the flow is stationary. As the flow expands, we assume that micro instabilities and turbulence constantly rearrange the field. As in the pure particle pressure case, the flow can go through a critical point, where the radius R has a minimum and beyond which the flow will become self-similar (if the external pressure itself behaves self-similarly with distance to the black hole) before the rest mass energy starts dominating the inertia, at which point the jet will reach a terminal Lorentz factor 1 . Along the way, the field might dissipate energy via reconnection- like processes, and radiation drag might alter the dynamics. We assume that no energy or particles are exchanged between jet and environment, except for radiative losses. However, the momentum discharge (the jet thrust quantities like 0 , U 0 i Q) need not be conserved along the jet. By assuming that hB 0i2i=8 (where a prime denotes that the quantity is measured in the comoving frame) do not vary significantly across the jet we simplify the analysis to a quasi1D solution. We ignore effects of shear at the jet boundaries. We assume throughout most of this chapter that the advected matter is cold (i.e., enthalpy density h0 n0mparticlec2 ). We are looking for stationary flow along the jet (i.e., far from the terminal shock), enabling us to drop time derivatives. Finally, to make this quasi 1D treatment possible, we will need to make the assumption that the jet is narrow, which in our case implies that the opening angle is small compared to the beaming angle, i.e., dR=dz 1= . As we will later show, this also implies that the jet is in causal contact with its environment (as required by the assumption that the jet is in pressure equilibrium with the surrounding medium). 2.2.1 Treatment of Magnetic Field We will use cylindrical coordinates (r; ; z ) with the z -axis oriented along the jet axis. The flow velocity is not aligned with the z -axis for r > 0 (the jet expands). We assume that the 31 Figure 2.2: Cartoon of the general picture employed in this chapter. Tangled magnetic field is generated in the disk, advected inward by the disk flow, and accelerated away from the black hole to form an initial outflow. Under suitable conditions, this outflow is then collimated and accelerates away from the core, keeping pressure balance with the thermal pressure provided by the jet environment. 32 sideways velocity is small compared to vz but non-vanishing, i.e., the flow is well collimated. e e The magnetic field is expressed in a different basis, since the standard basis vectors r and z 6= 0. One axis of this new basis is aligned with the local velocity vector, ek . The second unit vector e is coincident with the -unit vector of the lab coordinate system. The third unit vector e$ is obtained from the cross product of the are not orthogonal in the comoving frame for r other two. In the comoving frame we have B0 = B 0$ e$ + B 0e + B 0k ek: (2.2) As mentioned before, the 1D approximation is only possible if the opening angle is small compared to the beaming angle. This is because the Lorentz factor will not be nearly uniform across the jet otherwise. The assumption that dR=dz 1= simplifies the equations of motion significantly. Following B95, who investigated similar jets in the non-relativistic limit, we assume that the magnetic field is highly disorganized. In the comoving frame, averages over the individual components and cross terms vanish while the energy density in the individual components is not zero: hB 0iB 0ji = 0; for i 6= j; h B 0 i i = 0; hB 0i2i 8Ui0 6= 0: (2.3) Lorentz transformation of the field to the lab frame (and to the cylindrical coordinate system aligned with the jet axis) yields B= vz 0 v v B $ + r B 0k ^er + B 0^e + z B 0 k v v v vr 0 B $ ^ez : v (2.4) Some of the components are now correlated. The electric field in the lab frame is E = vz 2.2.1.1 B 0^er p vr 2 + vz 2 B 0 $^r vr B 0^ez : (2.5) Magnetic Equation of State Without the presence of turbulent rearrangement of the field, flux freezing would govern the behavior of the individual components. If we assume the presence of turbulent mixing 33 between the different field components, we might expect the field to follow a modified evolution according to dB 0 i = X j X @B 0 j @B 0 j d ( v ) + dR; ij ij @ v @R j (2.6) where the subscript ff denotes the value the derivative would take under flux freezing, and ij and ij are arbitrary mixing coefficients. Note that we assume that large scale field produced by shear (for example due to a boundary layer) will be tangled and cascaded to small scale turbulent field. We also assume that the effects of turbulent kinetic energy are negligible (an assumption that should be lifted in future, more realistic prescriptions of this model). Based on this picture we therefore choose the following convenient ad-hoc parametrization of the field evolution with Lorentz factor B 0 $ 2 / B 0 2 / (v ) and jet radius R, including rearrangement: 2+1 R 2+2 ; B 0 k 2 / (v )3 R 4+4 : This is the magnetic equation of state we use. In the case of pure flux freezing, i In the case of a completely isotropic field we have 1 (2.7) = 0 for all i. = 2=3, 2 = 2=3, 3 = 4=3, = 4=3. Note that this prescription is still fully general [until we make some limiting assumptions about the i (r; z )]. Since the re-arrangement process mixes the perpendicular and parallel components of the field, we would expect that the field behavior is changed from flux freezing in such a way that the coefficients i are bracketed by the values they take in the case of flux freezing.1 Since the case of a purely isotropic field must be included in our analysis, it is clear that this condition requires that 2 < 0 < 1 and 3 < 0 < 2 . We define two quantities to characterize the anisotropy of the magnetic pressure: U 0 U 0? 0k ; U k + U 0? 1 U 0 U 0$ Æ 0 ; U + U 0$ (2.8) Fully developed, compressible MHD turbulence is still an open and very difficult problem. Sridhar and Goldreich (1990); Goldreich and Sridhar (1995, 1997) have provided advanced treatment of this problem in the context of anisotropic incompressible MHD turbulence. They do find that turbulence tends to be anisotropic in the sense that the turbulent cascade might propagate a preferred field directionality to smaller scales. The situation considered in these papers is different from the one considered here in that we assume that no ordered large scale field is present and the fact that the plasma is internally relativistic and compressible. It would be an important step forward to generalize the results by Goldreich and Sridhar to the parameter choices considered here. 34 where U 0? U 0$ + U 0. purely parallel for toroidal for Æ = 1. Thus, the magnetic field is purely perpendicular for = 1, and = 1. The perpendicular component is purely radial for Æ = 1 and purely The field is perfectly isotropic for = 1=3 and Æ = 0. It is obvious from equation (2.7) that Æ is constant for any combination of parameters, since U 0 $ / U 0 by assumption. While this parametrization alone is rather unrestrictive, we can limit it to a one parameter family by assuming that the i are constants under any possible variation of and R, and that the rearrangement process does not change the total comoving energy density in the magnetic field. (Otherwise the same process would have to act as an energy sink, since we assume that the magnetic field is the dominant term in the internal energy budget. We would therefore be dealing with a dissipative process, which we will address in x2.2.1.2.) We can solve for i in terms of by fixing either or R and demanding that the total energy density U 0 P U 0i behave the same as it would following flux freezing: dU 0 = U 0 ? [(1 2) d( v) + (2 2) dR] + U 0 k [3 d( v) + (4 = for arbitrary d( 2U 0 ? (d( v) + dR) 4U 0 k dR 4) dR] (2.9) v) and dR. Constancy of any of the i then implies constancy of and substi- tution of from equation (2.8) yields Ui / ( v ) 1 R 3 1 = 1 + ; 2 = 1 ; 3 = 1; 4 = 1 (2.10) which includes the isotropic case, where the magnetic field behaves like a relativistic gas, for which = 1=3, Æ = 0. It turns out that one can find special analytic solutions with constant i that satisfy equation (2.9) without the requirement that be constant (see x 2.4). For these solutions the rear- rangement process conserves the comoving magnetic energy density only under the variations 35 in and R allowed by the Bernoulli equation [i.e., d( v) and dR in equation (2.9) are not arbitrary]. The only condition on the parameters i for such a solution is that 1 =2 = 3 =4 . These solutions are limited to the self-similar range, where the jet is dominated by magnetic pressure. Once they approach the terminal phase (i.e., 0 > U 0), the parameters i must vary with z . For the rest of this chapter we will assume that equation (2.10) holds unless indicated otherwise. 2.2.1.2 Dissipation of Magnetic Energy It is unlikely that the tangled magnetic field evolves without any dissipation of its energy (e.g., via reconnection). We thus include a simple, ad hoc prescription of magnetic energy losses. We base this parametrization on the idea that the magnetic field is always in a nearly force-free equilibrium. However, it is impossible to maintain perfect force-free conditions everywhere and as the jet expands in either direction, the field responds by rearrangement between the different components (eq. [2.10]) and by dissipation of some of its energy. We therefore assume that the dissipation rate is roughly proportional to the divergence of the velocity in the comoving frame: @U 0 i U 0 i r v0 @ diss (2.11) or, in the lab frame @ @U 0 i U 0 i ln vR2 : @z diss @z (2.12) This ansatz can easily be generalized to different i for different field components (e.g., if the Alfvén velocity factors into ). For a more realistic dissipation model see the Appendix. We will assume that the dissipated energy goes into isotropic particle pressure, which is then either (a) radiated away immediately as isotropic radiation in the comoving frame or (b) accumulated until the jet reaches a state of equipartition between particle pressure and magnetic field. 36 2.2.2 Equations of Motion Let us write the relativistic continuity equation as 0 vz R2 = const: (2.13) The energy and momentum equations are given by T ; = 0, (T is the stress-energy tensor, separable into a matter and an electromagnetic part). In the absence of gravity, this T ; = 0, which will be sufficient for the analysis through most of this chapter reduces to since most of the acceleration will likely take place at distance z rg GM=c2 , where M is the mass of the central black hole. It turns out, however, that gravity is important in discussing the critical points of the jet, in which case we will approximate the covariant derivative by a Newtonian potential ( 0 30 = 3 33 3 = 00 rg =z2 ). We will comment on the accuracy of this approximation in x2.3.1. Since there is no energy exchange between the jet and the environment, using the expression for the electromagnetic field measured in the lab frame from x2.2.1, we write the energy equation as T 0 ; = 0 (neglecting gravity). We then integrate the equation over a cross-sectional volume of the jet and convert it to a surface integral using Gauss’s law. The contribution from the sidewall is zero, giving 2 0 c2 + 4p0 vz R2 + (where the 1 v 4 z 2 B 0 2 + B 0 $ 2 R2 L = const: B 0 i 2 are now averaged quantities). (2.14) Dividing equation (2.13) into equation (2.14) gives the relativistic Bernoulli equation. In the more general case including radiative losses and gravity we have ! B0 2 d 2 2 02 vz R c + 4p0 + 2 ? dz 8 rg 2 2 0 2 +2 2 vz R c + 4p0 + 2U 0 ? + Srad = 0; z (2.15) where Srad is the energy lost to radiation leaving the jet. We have to make some assumption about the form of Srad , i.e., the amount of energy radiated away [cases (a) and (b) from x2.2.1.2]. 37 The z -momentum flux Q can be calculated in much the same way (integrating T 33 across a jet cross-section). Since the jet can exchange z -momentum with the environment, the momentum discharge need not be conserved, however. Dropping terms of order vr 2 , the integration yields Q Z A 2 v 2 R2 ( + 4p0 =c2 ) + R2 p0 dT 33 + R2 h 2 1 + v2 U 0 ? i U 0k : (2.16) The sideways momentum equation is given by T 1 ; the solution be stationary (i.e., vr T 0 ; = 0. The condition that @R(z )=@t = 0) gives the pressure balance condition between the jet and its environment. We assume that the internal structure of the field adjusts to maintain the given cross-section. Since we assume that vr @ small, @r vz , the internal variation will be sufficiently vr @ vz @z , to justify the assumption of uniformity (note: this assumption is only satisfied if the jet is in causal contact). We are thus only interested in the pressure balance condition at the jet walls, r = R, which gives pext = U0 + Uk0 U$0 + p0 : Note that (2.17) U$0 = 0 directly at the jet boundaries, since the magnetic field is assumed not to penetrate the contact discontinuity. However, since interior pressure balance demands that U0 + Uk0 U$0 + p0 be constant, we can set U0 U$0 = const: and substitute it for U0 at r = R, which gives equation (2.17). 2.3 Dynamical Solutions Before we start analyzing the equations presented above, it is worth noting that in the case of a cold (p0 = 0) jet and a magnetic field following pure flux freezing (1 = 2 = 0) the only possible solution to equation (2.14) far away from the core (i.e., z rg ) is (z) = const:, i.e., the jet expands sideways to satisfy pressure balance, without accelerating. This is because both the kinetic energy flux and the Poynting flux do not vary with R, while they do vary with 38 v, so that equation (2.14) becomes an equation of only. Thus, fixing the total jet power L fixes . While a scenario like this might explain the coasting phase of the jet (where no more acceleration occurs), it cannot account for the initial bulk acceleration we are looking for. Note that this is different than the case of anisotropic, relativistic particle pressure in the absence of isotropization (i.e., simply under adiabatic behavior of the individual components). In that case, the components scale like pz / ( v) 2 R 2, pr / p / ( v) 1 R 3 . We might expect a behavior like this for a relativistic turbulent pressure term. The sideways pressure is simply pr . At relativistic speeds, the solution approaches the one found by BR74, p /R/ 1=4 . Thus, unlike in the magnetic case described in this chapter, it is generally possible to accelerate a jet with anisotropic particle pressure without making any arbitrary assumptions about the randomization process. This is simply because only the perpendicular component of the field, U 0 ?, contributes to the Poynting flux, while all components of the pressure enter equation (2.14), which introduces a dependence on R, making a solution 6= const: possible. For a magnetically dominated solution to exist, on the other hand, we need a field rearrangement process at work, such as was described in x2.2.1.1. But even under such favorable conditions, a proper, accelerating solution is not always guaranteed. 2.3.1 Critical Points Since the jet will likely be injected with sub-relativistic speed, the question arises as to where the jet crosses possible critical points and at what velocity. If the jet is injected at large distances from the central black hole, we can neglect gravity; if it is injected close to the hole we will have to include at least a phenomenological gravity term. As a first step, we will set M = 0 artificially (still assuming the presence of an external pressure gradient) and neglect dissipation (Srad = 0). Equation (2.15) gives i dv 0 c2 + 4p0 + 2U 0 ? v2 + 4 (1 ad ) p0 + 2U 0 ? vdz dR = 0; + 4 (2 ad ) p0 2 (1 + ) U 0 ? Rdz 2 h (2.18) 39 where ad is the adiabatic index of the particles, ad d ln p0=d ln 0. This equation has a critical point when the expression in square brackets vanishes. At such a point, the jet crosssection must satisfy dR=dz = 0, i.e., the jet must go through a nozzle, the position and cross section of which are determined by the dynamics of the flow. Following the notation of BR74, the velocity at which that happens is s c? = 4p0 ? (ad 1) 2U 0 ?? ; 0 ? c2 + 4p0 ? + 2U 0 ?? where the subscript (2.19) ? indicates that the quantity is evaluated at the critical point z? . Since for a magnetically dominated jet lim !0 c? = 0, the critical point exists only for < 0. purely isotropic field, where = 1=3, c? reduces to the sound speed of a relativistic gas with For a p ad = 4=3, c? = 1=3. Locally we can always write pext /z , thus we define d ln pext =d ln z: (2.20) We can then substitute the pressure balance condition (2.17) into equation (2.18) in the limit 0 c2 + 4p0 U 0 and eliminate R, which yields 2 h i (3 + ) v2 + (1 + 3 ) dv = (1 + ) : vdz z (2.21) This equation also has a critical point with a critical speed of cy s 1 + 3 : 3 (2.22) Unlike equation (2.18), solutions cannot cross this critical point, since there dv=dz ! 1 (but see x2.3.2). We expect dpext =dz Since < 0, so solutions always accelerate (decelerate) for v > cy (v < cy ). cy only exists for < 1=3, solutions with > 1=3 always accelerate. equation (2.18) implies that for v > c? (v < c? ) the In that case jet is expanding (contracting) in the r-direction. Since c? only exists for < 0, solutions with > 0 always expand sideways. If, on the other hand, injected with v < 1=3, two branches of solutions exist: (a) solutions which are > cy , which always accelerate and go through a nozzle at v = c? cy , and (b) 40 solutions which are injected with v < cy , which always decelerate. Thus, at sufficiently large distances from the core for gravity to be negligible (see x2.3.2), highly anisotropic solutions with 1 have to be injected at relativistic velocities to be accelerating, since cy ! 1 as ! 1. This corresponds to the right branch of the dashed solutions plotted in Fig. 2.3 (which includes the effects of gravity, see x2.3.2). It is instructive to look at the case of pure anisotropic relativistic particle pressure again. (pk p?)=(p? + pk). If we fix p by some rearrangement process as we did for the magnetic field in x 2.2.1.1 (which might occur, for example, if We define the pressure anisotropy as p there is coupling between magnetic field and turbulent pressure as suggested by B95), the behavior is very similar in the sense that accelerating solutions for p have to be injected at super-critical velocity v If we simply let the components of arrive at a different critical velocity, cyp = in this case), which exists only for p q (2 + 2p )=(3 + p). solutions injected with Since c?p v > cyp q > cyp = (1 + 3p)=(5 p ). p evolve adiabatically (without rearrangement), we q (5 + 7p )=(9 + 3p ) (note that is not constant > 5=7. > cyp > 1=3 (i.e., for p? > 2pk ) for p The solution once again has a nozzle at c?p = > 5=7, and since dR=dz < 0 for v < c?p , must accelerate to satisfy pressure balance, which means that p increases with z , reducing cyp and thus making the flow more super-critical (i.e., once above the critical point, the solution moves away from it). 2.3.2 The Effects of Gravity on the Sonic Transition As seen in the previous section, a solution for > 1=3 that starts out with v < cy will always decelerate in the absence of gravity. However, as is the case in the solar wind, gravity can actually help a flow go through a critical point. We thus consider M > 0 in this section. A good overview of MHD effects in general relativity can be found in Phinney (1983). We can go through the same arguments as in x2.3.1. The critical speeds are still given by equations (2.19) and (2.22), but now the critical conditions are different. At c? , equation (2.15) 41 Γ†v† Γ*v* Γv 10 1 10 z† 100 z/rg 1000 Γv 10 1 z† 10 100 z/rg Figure 2.3: Inner solutions for = 2 in the vicinity of the critical point zy in the absence of dissipation but including gravity for the two possible cases, < 1=3 and > 1=3. In the first case (panel a), shown for = 0:9, the transonic solutions are thick black lines, suband super-critical solutions are thin black lines. Dashed lines show double-valued solutions (of interest is only the upper right quadrant for z > zy , v > cy ). The critical values cy , zy are shown as dash-dotted lines, c? is plotted as a grey dotted line. The condition dR=dz = 0 is shown as a dash-triple-dotted line and regions where dR=dz < 0 are shown as hatched areas. In the second case (panel b, for = 0) only super-critical solutions are possible. All solutions are expanding sideways and all possible initial values lead to acceptable solutions. We have once again indicated the location of zy . 42 gives 2r 2 dR 4p0 ? (2 2ad ) 2 (1 + ) U 0 ?? + 0 ? c2 + 4p0 ? + 2U 0 ?? g = 0 Rdz z? instead of dR=dz = 0. Since (2.23) 1 and ad > 1, we can infer that dR=dz > 0 at z? , i.e., there is no ‘geometric’ nozzle at z? anymore. The solution can always adjust dR=dz to satisfy this condition, thus the first critical point c? becomes irrelevant. Inclusion of the gravity term changes equation (2.21) to 2 h i (3 + ) v2 + (1 + 3 ) dv = (1 + ) vdz z (3 + ) 2rg : z2 (2.24) Now solutions can cross the critical point cy , since the right hand side of equation (2.24) vanishes at zy 3 + 2rg : 1+ v 6= cy If at zy , (2.25) dv=dz = 0 the solution must follow at that point. This is true for all . Since that is the only zero of equation (2.24), we can therefore conclude that solutions accelerating at any z > zy will accelerate for all z > zy . Solving the equations for dR=dz instead gives h 2 1 (3 + ) v2 + which also has a critical point at i cy . dR = Rdz For v2 + v = cy , + ( z 1) 2rg ; z2 the right hand side of this equation only vanishes at zy . In that case, dR=dz remains finite. For all other solutions (i.e., if z v = cy ), we must have singularities in both dv=dz (2.26) and dR=dz . 6= zy when The singularity in dv=dz evident from Fig. 2.3 and from equation (2.24); pressure balance then requires that must have a singularity of opposite sign, since dpext =dz is assumed to be finite, i.e. is dR=dz pext is continuous. We have numerically integrated equation (2.24) for two representative cases ( and = 0, = 2 ) = 0:9 and plotted them in Fig. 2.3. Solutions are qualitatively different for < 1=3 and > 1=3: 43 For < 1=3, there is one accelerating transonic solution, given by the condition in equation (2.25), shown in the upper panel of Fig. 2.3 as a thick solid black curve. This is also the only solution accelerating for all z . As in the case of a regular adiabatic wind (Parker 1958), there also exists a decelerating transonic solution. Regions where solutions contract in the r -direction (i.e., where dR=dz < 0) are shown as hatched areas. There are four more branches of solutions. Two branches are double-valued (shown as dashed curves in Fig. 2.3). The left branch of those solutions can be rejected since those solutions only exist for z < zy. branch to exist, it must be injected with For an accelerating solution on the right v > cy . This corresponds to the solutions discussed in x2.3.1 for which gravity can be neglected. The remaining two branches are solutions that are always sub- or supercritical (plotted as thin solid black curves in Fig. 2.3). The sub-critical solutions decelerate for large z and always stay sub-relativistic. They are uninteresting as possible candidates for relativistic jets. The supersonic solutions decelerate for z < zy and accelerate for z > zy. These solutions correspond to the super-critical solutions mentioned in x2.3.1. ! 1, zy ! 1. This is not necessarily an indication that no solution is possible for 1, since for those cases They always expand in the sideways direction. As we let the critical speed is very close to 1, thus the solution can attain large . Furthermore, as we saw above, the solution is expanding even before it goes through zy . We can thus have a regular (though sub-critical) accelerating jet even for For 1. > 1=3, there is only one branch of solutions, all of which start out decelerating, shown in the bottom panel of Fig. 2.3. As the solutions reach zy they begin to accelerate and behave the same way as described in x2.3.1. Since zy moves inward for increasing , this is no handicap. For > 1=3 we have zy < 8rg = from equation (2.25), which, for reasonable values of , is well in the regime where relativistic corrections become important and inside the region where we expect the injection to occur. All of 44 these solutions have positive sideways expansion dR=dz The transonic solution for > 0 for all z . < 1=3 has some additionally nice features: Since we know zy , we can relate the jet cross section to the total jet power Ly at zy . Assuming that the jet is still magnetically dominated at zy , the kinetic luminosity of the jet is Ly = Ry2 y2 vy2U 0 ?y : (2.27) The external pressure at zy is pext y and so Ry = v u u u Ly Æ t + 1+ 1 (1 + ) p : pext y (2.28) While we do not know pext y , for most parameter choices Ly is very nearly equal to L1 , which we have a reasonably good handle on from an observational point of view. Furthermore, we can estimate the jet width at observable distances and scale the solution back to gives us an estimate of py and thus U 0 ?y . This in turn will allow us to determine the original matter loading of the jet from estimates of the terminal Lorentz factor 2.4 zy , which 1. Solutions in the Self-Similar Regime and Asymptotic Solutions For an already relativistic jet in the ‘self-similar’ range zy is the location where 0 c2 (2.14) give /R z zinertia (where zinertia = 2U 0 ?) a self-similar solution can be found. 2 =1 and with equation (2.10) we have Equations (2.10) and / R. Under the conditions of equation (2.10), the pressure balance condition gives / R / pext 1=4 ; (2.29) the same as in the case of isotropic particle pressure considered by BR74. For future reference we define the acceleration efficiency d ln ; d ln pext thus for this simple case (2.30) = 1=4. 45 If we adopt the less limiting restriction 1 =2 = 3 =4 (see x2.2.1.1) instead of equation (2.10), we can find powerlaw solutions in three limiting cases: / R 2 =1 / pext 2 =41 , which can be very efficient for 1 2 . As pointed out in x2.2.1.1, one would generally expect that (a) For Æ = 0, the solution is given by 2 < 0 < 1 . 1, i.e., highly anisotropic, perpendicular fields, the solution is given by / R 2 =1 / pext 1=(21 =2 2) , which has a limiting efficiency of 1=2. (b) For (c) For If Æ 1 the solution is approximately the same as case (a). > 0, the solution will in general approach solutions (b) or (c) (i.e., ! 1). For Æ < 0 it is possible that the solution approaches a finite terminal Lorentz factor and zero opening angle if radial tension cancels the pressure due to Uk and U . Note once again that these solutions exist only for the coefficients that 1 1 , 2 , 3 , and 4 Fig. 2.4 shows the different regimes. 1 and c2 U?. For all other cases are not constant. Note that we would generally expect 2, since otherwise the re-arrangement process would be acting preferentially for changes in geometry in one specific direction, which seems arbitrary. Thus, these results reduce to the well known 1=4. We can look for solutions in the presence of dissipation of magnetic energy. We now have to consider equation (2.15). We assume that the energy goes completely into relativistic particles, thus energy conservation implies dp0 = dz dissipation 1 dU 0 : 3 dz dissipation (2.31) The particle energy can subsequently be radiated away as isotropic radiation. As long as p0 U 0 ?, the radiative case is no different from the non-radiative case, since the adiabatic term in the particle pressure does not contribute to the dynamics. A powerlaw type solution is once again possible only if the enthalpy is negligible compared to the magnetic energy density (see x2.4.2). In that case the solution in the self-similar 46 1.0 ζ → (−1) η → µ1/(2µ2 - 2µ1) δ 0.5 ζ → 1 η → −µ2/4µ1 0.0 ζ→(1+δ)/(1-δ) η → 0 -0.5 -1.0 0.1 1.0 -µ2/µ1 10.0 Figure 2.4: Regions in parameter space for the most general choice of parameters i possible in the self-similar region. We have indicated the various limits of at sufficiently low external pressure. Along with 1 we have indicated the limiting efficiency achievable when has reached is limiting value. For 2 =1 > 1, the efficiency can become very large. For Æ < 0, it is possible that the jet stalls due to radial tension. Note also that for Æ < 0 there is a minimum value for at the injection below which no solution is possible, given by min > (1+ Æ )=(Æ 1). Even if 0 > min , the solution will contract and decelerate if Æ is below a certain value. We have plotted this parameter range for a jet that starts out isotropically (i.e., with = 1=3) as a grey area. For smaller , this area will become larger. range is given by / pext = 1 at = 1. We have plotted with = 1=[4 + 6(3 + 5 )=(3 3 2 as a function of and 2 6 )] 1, with in Fig. the efficiency is larger than in the case without dissipation, for 2.5. For > 3=5 it is smaller. limiting efficiency that can be achieved in such a jet under the condition that given by < 3=5 The dR=dz > 0 is 1=2, as ! 0. This happens because the dissipative process can convert energy in the parallel field component Uk (which does not enter eq. [2.14]) into particle pressure, which must be taken into account in the energy balance. Also shown are areas in --space where the 1 2 5 -4 .3 0 47 0.25 0.40 0.50 1.00 0.1 0 0.2 0 0.30 Λ 0.10 dΓ/dz < 0 dR/dz < 0 d(αo/αb)/dz > 1 for: 3<ξ<4 2<ξ<3 ξ<2 0.01 -0.5 0.0 ζ 0.5 Figure 2.5: Contour plot of acceleration efficiency d ln =d ln pext for radiative dissipation and different values of and . The grey areas indicate parameter values for which the jet is either not collimated (light grey with dark grey border) or decelerates (dark grey with light grey border). The hatched areas indicate regions where the ratio o =b of opening angle to beaming angle grows with z for given values of 0 < < 4. conditions d =dz > 0, dR=dz > 0 are not satisfied. Note that the actual acceleration is not limited by the dissipative process: highly anisotropic fields with strong dissipation can produce faster acceleration, however, such cases are actually contracting in R, thus we do not consider them here. While dissipation can produce strong magnetic pressure gradients, the inherent assumption of a stationary jet, which leads to the condition of sideways pressure balance, restricts the run of pressure in the jet. If the energy is dissipated too fast, the jet will fall out of causal contact with itself and its environment and time independence would no longer be a good assumption. 48 2.4.1 Opening Angles and Causal Contact Since a jet is generally defined as a collimated outflow, we can ask under which condi- tions the solutions from above are actually collimated. The collimation condition dR=dz < 1 d ln pext =d ln z = < 4 as long as the jet is magnetically translates to a pressure gradient dominated, the same as in the particle pressure dominated case. The presence of dissipation can alter this value. Generally, the collimation is increased by dissipation, since the sideways pressure is reduced, thus the jet does not need to expand as much. In the coasting phase, where the jet is no longer accelerating, this condition changes to < 3 + < 4. Given the solutions from above, we can investigate the ratio of the opening angle o to the beaming angle b o =b = dR dz 1 . In the absence of dissipation we can write / z=2 1 ; (2.32) independent of . Thus, for steep pressure gradients > 2, the opening angle will grow faster than the beaming angle and will thus always become larger even if it starts out being smaller. For shallow pressure gradients < 2, the situation is reversed, i.e., the beaming angle will eventually become larger than the opening angle. The presence of dissipation changes this behavior qualitatively: the ratio o =b now depends on both and , as illustrated in Fig. 2.5. This has consequences for the appearance of the jet, since the effective beaming angle is given by the larger of the two angles. Under the assumption that the jet is always collimated, the opening angle in the coasting phase will always become smaller than the beaming angle, since the jet does not accelerate anymore. This could have important consequences for the morphology of superluminal sources: if the beaming angle were smaller than the opening angle, one might expect to see larger jet misalignments, or lose the jet morphology altogether. The appearance would become sensitive to the emissivity and local Lorentz factor as a function of position across the jet cross section. Jets that expand too fast will eventually lose causal contact with their environment. This happens when the Alfven crossing time of the jet becomes larger than the expansion time (in 49 the comoving frame), i.e., when R p0 z > 0 exp = 0 vAlfven c vdp =dz c (where we approximated vAlfven c) or R 0A = R> (2.33) z : (2.34) This corresponds (up to the factor ) to the criterion when o > b . Thus, for > 2 (in the absence of dissipation) the jet will eventually lose causal contact with its surroundings (see Fig. 2.5 for values of and where this is the case). As mentioned in x2.2, a quasi 1D treatment is no longer possible, since the internal pressure balance is now regulated by shocks traveling inward from the jet walls. After the jet reaches the terminal phase, it will re-gain causal contact, since the opening angle will continually decrease (assuming the jet is still collimated). 2.4.2 Equipartition Constant pumping of magnetic energy into particle pressure can lead to equipartition between U 0 and p. We can use the self-similar solution to estimate eq , where the accumulated particle pressure surpasses the magnetic energy density (including effects of adiabatic cooling on the accumulated particle pressure, where we assume that it behaves as a relativistic gas, 1> eq the solution might be altered. For some parameter values p never reaches the level of U 0 ? . In that case we estimate which gives an upper limit on the resulting pressure). Thus, for the asymptotic ratio (p0 =U 0 ?)1. Figure 2.6 shows the results of those estimates. For large , equipartition can be reached quickly, thus, unless the energy going into particles is subsequently radiated away, the assumption that the particle pressure be negligible compared to the magnetic field energy density will be violated beyond eq . We define the energy distribution function as f ( ) F0 s; Z 2 1 f ( )d = n0 ; (2.35) 4 e6 5 3 -2 .1 0 50 1.00 0.5 0.3 Λ 0.2 0.10 2 4 10 1.0 0.1 100 1e 6 1e4 0.01 -0.5 0.0 ζ 0.5 Figure 2.6: Value of for which the pressure accumulated by non-radiative dissipation reaches equipartition with U 0 ? . Neglecting p is no longer justified beyond that . For < 0:6 the pressure never catches up with U 0 ? , in that case we plotted contours of the limiting ratio p0 =U 0 ? (dashed lines). The hatched and grey regions correspond to the regions in Fig. 2.5. where is the Lorentz factor according to a particle’s random motion, measured in the comoving frame, and 1 2 are the lower and upper spectral cutoffs. Since we assume that the magnetic field is dominating the internal energy budget, synchrotron losses can be very strong, provided the particle energy spectrum is flat enough so that most of the energy is at high particle energies (i.e., s < 2). In that case we can expect most of the energy to be radiated away immediately and the corresponding electrons will lose most of the inertia, thus the dissipated energy will not lead to a build-up of particle pressure. If, however, synchrotron losses are weak compared to dissipation (e.g., if the spectrum is too steep, or if synchrotron self-absorption traps most of the radiation to inhibit cooling), the effects of particle pressure can become important, as demonstrated in Fig. 2.6. For a discussion of the observational effects of the different 51 radiative scenarios see x2.5.1 2.4.3 Full Solutions We can solve the full equation (2.15) in the regime 1, i.e., for relativistic jets. As mentioned before, the pressure balance condition leads to a simple algebraic equation in and R. In the absence of dissipation and gravity, equation (2.14) is in fact another algebraic equation relating and R, thus, the two equations can be solved for (pext ) using a numerical root finder. Apart from reproducing the scaling behaviors established in x2.3, this will enable us to determine the terminal Lorentz factors and the length scales over which the transitions between different dynamical phases occur. Furthermore, we can use the full dynamical model to investigate the evolution of such observational quantities as polarization and synchrotron brightness. In the absence of dissipation, the terminal Lorentz factor that can be reached with such a jet is simply lim!0 = 1 pext ! 0 0 0 c2 + 2U?0 0 + 4p0 0 ; 0 0 c2 (2.36) where subscripts 0 denote quantities evaluated at some arbitrary upstream point. This simple solution is no longer possible in the presence of dissipation, which introduces a sink term into equation (2.14). As a result, we have to use equation (2.15) instead. Once the energy has been converted into particle pressure, it can be radiated away as isotropic radiation, which will not affect the dynamics of the jet any further (assuming that p is dynamically unimportant). If the energy is stored as particle pressure, the pressure could eventually become dynamically important (see x2.4.2). Until that happens, though, the two solutions are identical. The terminal Lorentz factor is always reduced (see x2.5.1), but the acceleration efficiency can be increased for < 3=5 (see x2.4). We have plotted the solution for the radiative case (the one case solvable analytically) in Fig. 2.7. 52 Γ(z)/Γ0 Terminal Γ for Λ=0 10 pure magnetic jet (self similar case) cold matter (2Uperp=40ρ0c2) cold matter, dissipation for Λ=0.05 cold matter, dissipation, radiation drag 1 1 10 100 103 (z/z0)(ξ/2) 104 105 106 Figure 2.7: Analytic solutions in the limit v 1 for = 0: a) self similar limit, valid for very large U?0 0 c2 ; b) solution with cold matter, U?0 =0 c2 = 20, i.e., 1 = 41; c) radiative dissipation with = 0:05, otherwise same parameters as b); d) same parameters as c) but including radiation drag. Note that the dissipation of energy alters both the acceleration efficiency and the terminal Lorentz factor 1 . 2.4.4 Radiation Drag The presence of ultra-high-energy particles in AGN jets suggests that inverse Compton (IC) enhanced radiation drag might be dynamically important. While O’Dell (1981) initially suggested that pair jets might be accelerated by the Compton rocket effect, Phinney (1982) showed that it is hard to accelerate a plasma beyond fairly modest Lorentz factors by radiation pressure without a continuous source of particle acceleration to offset the strong IC cooling of the plasma. Furthermore, if the radiation source is not point-like, the terminal Lorentz factor is limited by the solid angle the radiation source subtends. On the other hand, radiation drag can hamper the bulk acceleration of plasmas containing relativistic particles in the presence of 53 a radiation field, if those particles are continuously reheated to overcome the IC losses. The dissipation mechanism discussed above could provide such reheating. Here we will consider the effect of radiation drag in the simplest possible prescription. We assume that the IC cooling and the dissipational heating time scales are short compared to the adiabatic timescale. If this is not satisfied, the influence of radiation drag will be reduced. We can then expect dissipational heating to nearly balance IC losses in a near equilibrium situation. Thus the amount of IC drag is controlled by how much dissipation there is. For this approximation to be valid, IC losses must dominate the loss processes of the particles, i.e., the radiation energy density magnetic field energy density U 0 rad in the comoving frame must be large compared to the U 0 (for large enough this is always going to be the case, since the external field will be Doppler boosted). Finally, we assume that h 2 2 i 1, where is the particle Lorentz factor in the comoving frame. This sets an upper limit of U 0 rad 6 103 ergs cm 3 " U 0 d ln R2 1014 cm 02 c d ln z z # (2.37) on the comoving radiation energy density (otherwise IC cooling would have lowered the upper spectral cutoff to 2 1). These assumptions allow us to eliminate U 0rad from the equations, since the drag term and the cooling term are both proportional to U 0 rad . In a sense, then, we are presenting an upper limit on the importance of IC radiation drag over large length scales. It has to be kept in mind, though, that drag can be much more important in non-stationary situations (like, for example, in shocks), which are beyond the scope of this thesis. We assume the jet is moving through a radiation field that is locally isotropic in the lab frame. Following Phinney’s treatment (1982), we can calculate the loss rate and the force density due to IC scattering in the comoving frame and then transform back to lab frame to find the additional term for equation (2.14). We find that radiation drag always decreases both the acceleration efficiency and the terminal Lorentz factor 1 by moderate amounts. It does not, however, introduce qualitatively new features. To demonstrate this, we have plotted a solution including radiation drag for otherwise identical parameters in Fig. 2.7. 54 2.5 Discussion 2.5.1 Tradeoff Between Dissipation and Acceleration and Synchrotron Brightness In the following section we will investigate the observational effects of the jets we have introduced in this chapter. A highly dissipative jet will radiate away a large fraction of its internal energy along the way before reaching the terminal Lorentz factor 1 , while a non- dissipative jet will convert all its internal energy into kinetic energy flux. Since the jet will ultimately terminate and reconvert its kinetic energy flux into random particle energy when it slams into the surrounding medium, the ratio of kinetic luminosity (which could be estimated based on the energy input into the lobes, based on the source size and its age) to the radiative luminosity Ldiss (z ) (i.e., the integrated luminosity of the jet before reaching the terminal shock) should give us some indication of the importance of dissipation. We have already seen in x 2.4.3 that the presence of dissipation can lower lowering the kinetic energy flux at the terminal shock, 1, thus L1 (dominated by cold kinetic energy flux), and the produced hot-spot luminosity. A given fraction b of the terminal luminosity bL1 will be radiated away, which can be estimated from the hot-spot and cocoon luminosity (calculating b is, of course, a highly non-trivial matter), giving us a handle on . We have plotted the ratio Ldiss L1 (2.38) in Fig. 2.8. To make that plot, we chose parameters such that in the absence of dissipation the jet would reach 1( = 0) = 2U 0 ?0 =(0 0 c2 ) = 100. If we had chosen a larger (smaller) value of this parameter, the lines in the plot would move down (up), since 1 depends non-linearly on both and 2U 0 0 =(0 0 c2 ), so this plot is only a representative one of a family of similar plots for different 1 ( = 0). Another question is what the spatial distribution of the jet emission is, since there are several competing effects: the optical depth to self absorption (and inverse Compton up-scattering), .4 0 -1 5 2 6 55 100 25 5 625 1 25 10-1 Λ 1 0.2 10-2 0.04 10-3 -1.0 -0.5 0.0 ζ 0.5 1.0 Figure 2.8: Plot of the ratio Ldiss =L1 , indicating how much of the energy carried in the jet is radiated away and how much will reach the terminal shock (this energy can be used to heat the hot spot and to inflate the radio lobes). This plot was constructed for 10 1 ( = 0) = 100. Lower values of 10 will shift the lines in this plot upwards. Note that this plot was constructed using the assumption that all the dissipated energy is radiated away on the spot. Doppler boosting and opening angle (the larger of which will determine the opening angle of the cone into which most of the radiation goes), and of course the dissipative power of the jet itself [depending on and (z ), R(z )]. This question can be asked with respect to the frequency in- tegrated brightness I or the spectral brightness I . If we assume that all the dissipated energy is radiated away on the spot, we can calculate the local dissipation rate, which must then be equal to the local frequency integrated jet emissivity j 0 in the comoving frame. This assumption de- pends on the injected particle energy spectrum. If the spectrum is flatter than s = 2, most of the energy is in the high energy particles. In that case, synchrotron cooling can be efficient enough for our assumption of on the spot radiation to be effective. If, on the other hand, s > 2, most of the energy is in the low energy particles, synchrotron radiation will not be efficient (unless 1 56 is very high, in which case the injected spectrum would rapidly cool to a quasi mono-energetic distribution), and the jet will accumulate particle pressure or radiate by other means (note that Compton cooling would be equally insufficient to balance heating in this case). To investigate the first case we will set s < 2. Given a viewing angle we can then determine the observed total intensity I , given by I/ where dU 0 dz diss D2 R ; sin (2.39) is the angle between line of sight and jet axis and [ (1 v cos )] D 1 is the Doppler factor. This expression takes relativistic beaming and the relativistic corrections to foreshortening into account. One might expect that the integrated brightness peaks at a certain distance from the core, since D is strongly peaked at 1=. However, in our prescription the dissipation drops off too fast for this effect to be important. The main difference in the brightness evolution is that a dissipative jet has a different efficiency and generally expands less rapidly in the sideways direction (and will reach a smaller terminal Lorentz factor effect will become important once the jet has reached 1 ). This 1 and only for large enough to signif- icantly alter the dynamics ( > 0:1). We have plotted I as a function of z for different values of , = 0, U 0 0 = 20 0 0 c2 , and a viewing angle of = 10Æ in Fig. 2.9, arbitrarily normalized to I ( = 0:01) to increase dynamic range (the brightness decreases by many orders of magnitude along the jet). As is obvious from the plot, for small , only the overall normalization of I varies with , whereas for large enough , the brightness distribution itself changes shape due to the altered dynamics. Also shown are the Doppler factors D for the different parameters, which are primarily responsible for the different shapes. The situation can become more difficult in the opposite case, i.e., if most of the radiation is trapped (e.g., by synchrotron self-absorption, which implies a steep spectrum, s > 3) or if the deposited energy is simply not efficiently radiated (e.g., if 2 < s < 3). In that case the emission of dissipated energy could be delayed, leading to a relative brightness peak downstream. To briefly investigate this possibility, we assume the latter case, i.e., 2 < s < 3, which is not an 57 10 D I(Λ)/I(Λ=0.01) 100 1 Λ=.004 Λ=.010 Λ=.027 0.1 1 10 100 Λ=.074 Λ=.200 Λ=.541 103 z/z0 104 105 106 Figure 2.9: Plot of the frequency integrated brightness for a radiative jet (i.e., all the dissipated energy is radiated away on the spot) as a function of z for different values of , = 0, = 2, U 0 ?0 =00 = 20, and = 10Æ , arbitrarily normalized to the intensity curve for = 0:01 to increase the contrast (thick black curves). Also shown are the corresponding Doppler factors D as thin grey curves. The shapes of the individual intensity curves are mainly determined by the variation of D . Note that a significant observable effect is achievable only for > 0:1. unreasonable choice for AGNs (see x2.5.3, for example). We assume that the energy flux F peaks at high energies p : either at the spectral break of 1=2 expected in a scenario in which high energy particles are constantly re-injected, where the spectral index is given by d ln I ; d ln (2.40) or at the spectral cutoff produced by synchrotron and IC cooling (in the absence of a strong break). The position of p depends on adiabatic effects, radiative cooling, and heating due to dissipation. The spectrum will be self-absorbed at low frequencies, which generally leads to an observed spectral index of 5=2 (for an exact treatment of the spectral shape at the self absorption turnover see De Kool, Begelman, and Sikora 1989). If we take 2 < s < 3 or 58 1=2 < < 1, the self absorbed part contributes a negligible fraction to the total brightness and most of the energy is emitted at the high end of the spectrum. In this case it is impossible to calculate the brightness analytically as a function only of , R, and z . Rather, one can numerically integrate the evolution equation of the peak frequency under adiabatic cooling, dissipative heating [we assume a self-similar transfer of energy from magnetic field to the particles such that ing on the basis of the solution (d=dz )jdiss / (dU 0 =dz )jdiss], and synchrotron cool- (z ) given above. We can estimate the run of I by scaling it with the brightness at p , taking account of relativistic beaming and aberration. If we choose to normalize the intensity curves as we did in the previous case, we can get around fixing the absolute normalization of U 0 , since it only enters linearly into the intensity and will thus cancel out upon normalization. We used U 0 ?0 = 20 0 0 c2 , along with s = 5=2 and plotted the fre- quency integrated intensity in Fig. 2.10 with otherwise the same parameter values as in Fig. 2.9, once again normalized to I for = 0:01. Note that for large values of our assumption that the jet be magnetically dominated and that particle pressure be negligible can break down (see Fig. 2.6), so curves with high are to be taken with a grain of salt. Nevertheless, it is inter- esting to note that the intensity drops less rapidly with z for larger values of , corresponding to the delayed emission mentioned above. The shapes of these curves depend only weakly on s. The different bends in the curves stem from the evolution of the Doppler factor (shown in Fig. 2.9), and the evolution of the peak frequency. The slopes of the curves are produced mostly by the evolution of the lower cutoff frequency 1 (see eq. [2.35]), which enters the expression for the synchrotron brightness through the powerlaw normalization of the particle distribution, and by the evolution of Lorentz factor and jet radius (entering through the particle density and the integration of the emissivity across the jet). 2.5.2 Polarization While the degree of polarization is highest for homogeneous magnetic fields, jets with tangled or disorganized field can exhibit a net polarization if there is a net anisotropy in the field 59 104 Λ=.004 Λ=.010 Λ=.027 Λ=.074 Λ=.200 Λ=.541 I(Λ)/I(Λ=0.01) 103 100 10 1 1 10 103 100 104 105 z/z0 Figure 2.10: Plot of the frequency integrated brightness for a marginally non-radiative jet (only a dynamically small amount of the dissipated energy is radiated away on the spot) as a function of z for different values of , = 0, U 0 0 =00 c2 = 20, = 2, and = 10Æ , arbitrarily normalized to the intensity curve for = 0:01 to increase the contrast (the absolute intensity drops by many orders of magnitude). Note that these curves do not depend on the absolute value of the magnetic field, which cancels out due to the normalization. (Laing 1980). The measured polarization will depend not only on , but also on the viewing angle and the bulk Lorentz factor . The polarization of radiation from a powerlaw distribution of electrons with index s in a region of homogeneous field is given by I I s+1 ? k = I? + Ik s + 7=3 (2.41) where I is the intensity at a given optically thin wavelength. To calculate the integrated polarization, we average across the jet. To do this we decompose the radiation into polarization along the jet axis and perpendicular to it. Furthermore, we assume that field directions are distributed among all solid angles and introduce a weighting function that distributes the field orientations 60 to the required anisotropy, w(#) = sin # (2.42) where # is the angle between the field and the z -axis and is determined by the anisotropy. We can solve for under the condition that hBk2 i = (1 + )=(1 = )hB?2 i: 1 + 3 : 1+ (2.43) We correct the viewing angle for relativistic aberration, which has a significant impact on the observed polarization, since the average polarization will go to zero for a jet seen head on. Furthermore, the angle between line of sight and magnetic field is important in determining the relative brightness of a region. Figure 2.11 shows the predicted polarization for the cases shown in Fig. 2.7, a spectral index of = 0:5, and a viewing angle of = 10Æ . Since the anisotropy of the jet is fixed, the variation in the polarization ( ) is solely caused by changes in the viewing angle due to relativistic aberration. Generally, the polarization will be perpendicular to the jet axis if < 1=3 and parallel if > 1=3. As long as equation (2.10) holds, an extremum () will be present and it should indicate the position where = 1= sin , i.e., where the viewing angle corrected for aberration is 0 = 90Æ . Note that this polarization is averaged in across the jet. In order to compare these predictions to actual measurements a relatively small correction for the emission weighted averaging across the jet at different angles must be made. The qualitative predictions of this section should be unaffected by that caveat. 2.5.3 Applications Finally, we sketch out some applications for this model. The best studied AGN jet is that in M87, since it is the closest unobscured source (though by no means a particularly powerful one). The properties of the M87 jet are discussed at length in x3, here we will only list the properties important for this analysis. The central black hole in M87 has a relatively well 2:4 109 M or rg 3:5 1014 cm. The kinetic power of M87 is estimated to be of order Lkin 1043 44 ergs sec 1 (Reynolds et al. 1996b, BB). Taking the determined mass of M 61 pure magnetic jet (self similar case) cold matter (2Uperp=40ρ0c2) cold matter, dissipation for Λ=0.05 cold matter, dissipation, radiation drag Π[%] 30 20 10 0 1 10 100 103 z/z0 104 105 106 Figure 2.11: Optically thin polarization as a function of z for the same parameter values as in Fig. 2.7 and a viewing angle of = 10Æ . We chose a spectral index of = 0:5. The variation in is solely due to changes in the aberrated viewing angle along the jet. proper motion measurements based on HST data (Sparks, Biretta, and Macchetto 1996, SBM hereafter) at face value, the terminal bulk Lorentz factor likely falls into the range2 10 with a viewing angle of 20Æ . The average polarization at kpc distances (where the jet has likely reached terminal velocity) is roughly corresponds to 6< 1< 10% parallel to the jet axis , which 0:3 with the numbers given above. Reynolds et al. (1996b) showed that the jet probably consists of pairs rather than ionized gas, so the jet might actually still be accelerating (if indeed a large fraction of the particles has > 10. Note, however, that the presence of shocks, clearly visible as knots in all wavelengths, calls for a more sophisticated model which takes time-dependence and MHD instability effects 2 Note that VLA measurement show slower proper motions (Biretta, Zhou, and Owen 1995) and the relationship between the observed pattern speeds and is not known. There are, however, no direct measurements of bulk motions, so for lack of better knowledge we will use the larger values obtained from the optical data. 62 into account. For a discussion of the nature of the shocks observed in M87 see BB.) Furthermore, there is evidence that the jet is not magnetically dominated on large scales (z > 100 pc) and that the magnetic field is actually somewhat below equipartition (Heinz and Begelman 1997, see x3), which means in this context that the magnetic field must have been dissipated non-radiatively, accounting for the particle pressure at larger distances. The observed spec- 0:6, which is at least in the correct regime for synchrotron radiation to be inefficient at radiating away the dissipated energy (see x2.5.1). At a viewing angle of 20Æ the jet radius at knot A (z 3 kpc) is R 35 pc with an approximate opening angle of o 0:7Æ , much smaller than the beaming angle of b > 6Æ , tral index at optically thin wavelengths is thus the jet is narrow at least at VLA resolution. Note that entrainment of ambient material may be important before the jet reaches knot A (Bicknell and Begelman 1996, BB hereafter). Using knot D as a reference point does not change this analysis significantly, however. There are no good estimates of the pressure gradient in the innermost regions of the M87 X-ray atmosphere (this situation should change, though, with upcoming Chandra observations of M87). The pressure at large distances is approximately pISM 10 10 dyn cm 2 , but BB argue that the pressure in the radio lobes is significantly higher than this, pext 1:5 10 9 dyn cm 2 . For lack of better information we will assume the latter value and a smooth pressure gradient with = const. The radiative luminosity of the jet itself is Lrad > 3 1042 ergs sec 1 (Reynolds et al. 1996b), which argues for > 4 10 3 . If (as we speculated above) much of the particle pressure at large distances was indeed produced by dissipation, could be much larger. The jet probably reaches terminal 1 10 somewhere between VLBI scales and VLA scales, 2 103 rg 0:2 pc < z1 < 200 pc 2106 rg . For small enough to be dynamically unimportant we can assume that 1=4 in the self similar regime. Arbitrarily setting z0 10 rg gives 0:8 < < 1:74. The central pressure p0 is then 2 10 4 dyn cm 2 < p0 < 200 dyn cm 2 , which requires an rms magnetic field of balance (using an assumed z0 0:09 G < B 0 0 < 90 G for pressure 0:3). The initial jet width strongly depends on : 8 rg < R0 < 9000 rg for = 10rg . The latter value is unrealistic (and inconsistent with the limits put on 63 the jet width by VLBI observations, Junor and Biretta 1995), since most of the energy output of the disk into the jet will be provided close to the black hole. It is therefore most reasonable to 2 103 rg and 1:7. The total jet power implied by the numbers given is of order L 2 1044 ergs sec 1 , consistent with the estimate by BB. Overall it seems that assume that z1 this model is consistent with the observed properties of M87 to first order if we adopt a pressure gradient following 1:7. The total isotropic energy output of E > 1054 ergs of GRB 990123 (Akerlof et al. 1999; Bloom et al. 1999) argues strongly in favor of non-isotropic gamma-ray burst (GRB) scenarios, so jet models explaining the apparently beamed nature of these sources (e.g., Meszaros and Rees 1997; Sari, Piran, and Halpern 1999) enjoy newly enhanced popularity. One of the standard scenarios for the energy sources of GRBs is a massive accretion event (either a neutron star ski, - neutron star merger or the accretion of a neutron star by a black hole: Narayan, Paczyn and Piran 1992), which leads to the formation of a disk after tidal disruption of one of the objects. Since neutron stars already display large magnetic fields, one might expect strong shear amplification of this field in the disk, leading to a scenario similar to what we described in x2.2. Similarly, the hypernova approach (Paczyn ski 1998; Woosley 1993) can produce a pre- collimated outflow, which might then evolve into a jet. Application of our model to GRBs is, however, not as straightforward as in the case of mature radio galaxies. This is because GRBs are highly time dependent (corresponding to the adolescent stages of radio galaxies): the lifetime of the jet (roughly of the order of the light travel time of the material) is shorter than the sound crossing time of the bubble the jet blows into the environment, so a pressure balanced solution as described above (which will be set up after the jet and the ambient material have equilibrated, i.e., after the jet has existed for a few sound crossing times) might not be a good approximation. The investigation of jet dynamics in the context of GRBs and in the framework of tangled fields as introduced above will therefore be the subject of future work. Here we simply wish to point out the benefits of jet models in general and an approach based on our model in particular: 64 Acceleration of GRB outflows by Poynting flux has the advantage that collimation can be provided not only by the external medium, but also by the field geometry itself (note that for Æ = 0 the perpendicular component of the field does not contribute to the sideways pressure, so for 1 the jet can have a large Poynting flux yet orders of magnitude smaller sideways pressure than a particle dominated jet would have for the same energy flux). One would not need to invoke shocks to produce emission in this context, since the internal dissipation of magnetic energy would provide a natural source of high energy particles and photons to produce gamma rays (see Thompson 1994 for an example of how internal dissipation can power GRBs). The short term variability seen in GRBs could then be explained by inhomogeneities (e.g., variations in the inhomogeneity of the field) imprinted on the outflow by variability in the central engine itself, which is expected to have time scales of the same order as the ones observed. 2.6 Chapter Summary In this chapter we presented an alternative jet acceleration model that utilizes tangled magnetic fields rather than organized fields. Collimation must be provided by an external agent, but magnetic tension can still reduce the amount of pressure needed to collimate the jet. Unlike jets accelerated by particle pressure or radiation pressure, radiative losses are not a severe constraint on this model, and it avoids MHD instabilities encountered in magneto-centrifugal jets. This model is similar to the original ‘Twin Exhaust’ model (BR74). Analytic solutions show that / pext 1=4 . Dissipation of magnetic energy can both increase or decrease the acceleration rate, while radiation drag will always slow down the jet. We calculated the change in the terminal Lorentz factor 1 due to dissipation and produced surface brightness, as well as polarization predictions for small scale jets. Finally, we demonstrated that the model is 65 consistent with the observations of the M87 jet. Future research is necessary to include the effects of turbulent kinetic energy, time dependence, 2D effects, such as shear layers, and the presence of large scale ordered magnetic fields. It seems most likely that a realistic jet contains both ordered and chaotic field and a combination of the magneto-centrifugal model with the tangled field model would be a more realistic approach. Chapter 3 Energetics of Jets and the M87 Jet It should be evident from the previous chapter that knowledge of the internal makeup of jets is critical to understanding the origin and acceleration mechanism of jets. Since resolution limits prohibit us from studying the innermost regions of jets directly, the only way to learn about the physical conditions in the plasma is from circumstantial evidence gathered at larger radii. If we can determine the magnetic field strength, its level of uniformity, and the nature of the particles (i.e., pairs vs. ions) are at large radii, we can then try to extrapolate backwards to pin down which of the acceleration mechanisms mentioned in x2 is at work. As it turns out, determining even such fundamental properties as the magnetic field strength in the jet is far from trivial. The most promising way to measure this particular (and particularly important) quantity is via measurements of particle evolution under the influence of synchrotron losses. To do this, resolving the jet at high frequencies (optical and preferably X-ray) is essential, which limits us to the most nearby sources. The nearest and best-studied AGN jet accessible at all frequencies is that in the galaxy Messier 87. In this chapter we will use the example of M87 to demonstrate how we can learn more about the energetics of AGN jets. The following work has been published in Heinz and Begelman (1997) and Heinz (1997). 3.1 The M87 Jet After 79 Years of Surveillance M87 is the central cluster galaxy and brightest member of the Virgo cluster. It shows the typical characteristics of a large elliptical galaxy (it has been classified as an E0 pec galaxy, 67 Sandage 1961) with a total luminosity of about 30 L . Recent distance measurements put it at a distance of 16 Mpc (Nielsen et al. 1999). Surface brightness measurements reveal a strong central peak in density (Young, Westphal, Kristian, Wilson, and Landauer 1978), suggesting the presence of a 109 M black hole at the center of M87. This hypothesis has been strengthened by HST observations of what appears to be an accretion disk around the central compact object, which reveals Doppler motion consistent with Keplerian rotation around a 3 4 109 M black hole (Ford et al. 1994; Macchetto, Marconi, Axon, Capetti, Sparks, and Crane 1997). The noticeable feature of M87 is its bright jet, visible all the way from radio to X-ray wavelengths. First observed by Curtis (1918), it has become one of the prototypical radio jets (mostly due to its proximity, since the radio galaxy itself does not particularly stand out from the crowd of modest power radio sources). The large scale structure of the radio source shows strong signs of interaction with the environment or non-steady behavior of the central engine, with size scales ranging from 5 kpc (VLA radio jet and lobes) to the large scale radio source (about 100 kpc). M87 has been classified as an FR I. Indeed, the total radio power of Virgo A is not overwhelming: Lradio 1042 ergs sec 4 1044 ergs sec 2 . The kinetic power, estimated to be roughly between 1043 and 1 (BB, Reynolds et al. 1996b), is similarly small compared to the Eddington luminosity of LEdd 1047 ergs sec 1 . This has led to the hypothesis that the central object in M87 is fed by an advection dominated flow (Reynolds et al. 1996a). Even though the jet in M87 has been observed in every possible wavelength band (Figures 3.1 and 3.2 show M87 in the radio, and optical bands), some puzzles remain about the nature of its emissivity and composition. Polarization observations at both optical and radio wavelengths have shown that the emission from the jet at wavelengths longward of 100 Å is most likely of synchrotron origin (Baade 1956; Owen, Hardee, and Cornwell 1989). Collimated structure can be traced back to terminates 0:01pc from the core (Junor and Biretta 1995), and 2500 away from the core (corresponding to a projected length of about 2 kpc at the assumed distance of 16 Mpc) in the western radio lobe, with optical emission still detectable at 68 Figure 3.1: Combined high dynamic range VLA map of the jet and lobes at 15 GHz and 0:00 15 resolution (Biretta 1993). this distance. The jet looks very similar at optical and radio wavelengths, although SBM show that differences (e.g., in the transverse brightness profiles) do exist. Reynolds et al. (1996b) argue that the jet plasma is very likely composed of electrons and positrons rather than heavier particles such as protons, but more conclusive evidence is needed to settle this question. Far from having a smooth appearance, the jet exhibits a series of bright knots at intervals roughly 2:00 5 apart (see Figure 3.1). The nature of the knots is uncertain, but they are usually attributed to internal shocks from either flow instabilities (BB) or variable outflow at the source (Rees 1978b). Figure 3.2 shows the sharp increase in brightness in the knot and its filamentary appearance, arguing against variable outflow as a source of the brightness variations observed. The lack of any emission or absorption features in the spectrum of the jet makes a direct determination of the bulk velocity of the jet plasma impossible. However, the onesidedness of the M87 jet has been interpreted as the result of relativistic beaming. Adopting a lower limit on the jet-to-counterjet radio brightness ratio of 150 (Biretta 1993), one can set a lower limit of jet 2 on the bulk Lorentz factor of the plasma with line of sight inclinations of LOS 35Æ . 69 Figure 3.2: HST FOC image (upper panel) and 2cm VLA map of the jet (lower panel), adopted from SBM. The bottom panel shows the distance from the core and the knot labels. Even though the dynamic range of optical HST images is larger than that achieved by Owen, Hardee, and Cornwell (1989), the constraints on jet and LOS (the dynamical parameters of the jet) set by the radio observations are stronger than what follows from the optical non-detections. This is because the brightness ratio goes as [(1 cos LOS ) = (1 + cos LOS )]3+ and R 0:5, the radio spectral index, is smaller than O 1:2, the optical spectral index. Doppler beaming of the counter jet emission away from the observer would explain the existence of the radio lobe on the eastern side of the core, for which no jet is visible. New infrared observations that detect emission from the counterjet region at the 3 level (Stiavelli, Peletier, and Carollo 1997) seem to confirm the hypothesis of relativistic beaming. The Doppler beaming interpretation is also bolstered by proper motion measurements of the knots (Biretta et al. 1995), which show characteristic velocities vproper 0:5 c in knots A and B, with some features exhibiting much larger proper velocities (a subfeature of knot D appears to show superluminal motion at a level of 6c, Biretta, Sparks, and Macchetto 1999). These motions broadly support the interpreta- tion of the knots as relatively weak, oblique shocks moving down the jet with pattern speeds 70 significantly smaller than the bulk speed of the flow (BB). Figure 3.3 shows the integrated spectrum for the knot A-B region (Meisenheimer et al. 1996), which is typical for the spectrum observed along the jet. Both the knots and the interknot regions exhibit a featureless power law spectrum of index R the optical data with a power law of index RO 1:8 in the optical. 0:5 in the radio, connecting to 0:65, and steepening to O between 1:2 and This steepening trend is also found in observations at infrared (e.g., Stocke et al. 1981) and ultraviolet (Perola and Tarenghi 1980) wavelengths, as confirmed recently by HST observations (Boksenberg et al. 1992, , SBM). X-ray observations made with Einstein Observatory (Biretta et al. 1991) and ROSAT (Neumann et al. 1996; Reynolds et al. 1996a) reveal X-ray emission from several spots along the jet (mainly the core and knot A, possibly also from knots D and B). However, the origin of the X-ray emission is unknown and it is not clear whether the spectrum breaks between optical and X-ray wavelengths to a spectral index of OX 1:4, with the X-ray emission still being of synchrotron origin, or whether the X-ray emission is produced by a different mechanism, such as inverse Compton scattering or bremsstrahlung. 3.1.1 The Spectral Aging Problem One might hope to detect the effects of synchrotron cooling and relativistic particle ac- celeration by studying the spectrum as a function of position along the jet. Such measurements (SBM) show that the radio–to–optical spectral index, optical spectral index, RO , is very nearly uniform, while the O , is anti–correlated with the brightness, i.e., the optical spectrum is flatter in regions of higher intensity. Modeling the optical steepening as a high-energy cutoff imposed on a power law spectrum, Meisenheimer (1999, hereafter M99) and Meisenheimer et al. (1996) find a corresponding correlation between brightness and cutoff frequency, i.e., a higher cutoff frequency at higher intensities1 . Both of these results are striking in the lack of a strong secular decline in the cutoff frequency with distance from the core, as would be expected 1 Appendix B reviews basic properties of synchrotron radiation and details of the model fit by M99. 71 Figure 3.3: Top panel: radio-to-optical spectrum for the integrated knot AB region. The radio-to-optical spectral index is RO 0:65, the spectrum cuts off at 1015 Hz. Bottom panel: optical-to-X-ray spectrum for the integrated knot A-B region. The origin of the X-ray emission is unknown. The spectrum could either exhibit a cutoff in the UV and have a separate component accounting for the X-ray emission or (if the X-ray emission is of synchrotron origin) it might break in the optical and connect to the X-ray with a OX 1:4 power law. From Meisenheimer et al. (1996). 72 naively if the steepening were due to synchrotron cooling. Indeed, these observational results do not compare well with simple quantitative models of synchrotron cooling in the M87 jet. The usual assumption of an equipartition between magnetic and particle energy density1 in the jet plasma leads to estimates of the magnetic field of order 300 G , with values up to 500 G in knot A. The synchrotron lifetime2 with Lorentz factors of only for electrons 106 needed to produce the optical emission in a 300 G field, is 2:3 1010 sec, which for mildly relativistic bulk velocities (e.g., 0:5 c) implies a travel distance of less than 120 pc. But the projected length of the jet is about 2 kpc, and even the distances between the most prominent knots are longer than the estimated cooling length. Yet the spectrum between radio and optical bands remains remarkably constant along the jet, with only minor variations in the optical spectral index. This presents a paradox: After a travel distance of 2 kpc one would expect the high energy particles to have cooled in such a way that the spectrum would drop very steeply above 1012 Hz. This cutoff frequency is a factor of 103 smaller than what is actually observed. The discrepancy becomes worse if the magnetic field is stronger than the equipartition value, as suggested by Owen et al. (1989) in order to explain the confinement of the overpressured jet via magnetic tension force. (An alternate explanation for the confinement — that the radio cocoon surrounding the jet is overpressured with respect to its surroundings — has been proposed by BB.) Three explanations for the discrepancy between the expected and the observed amount of cooling have appeared in the literature: (1) First-order Fermi re–acceleration3 in the knots, interpreted as shocks, could produce high energy electrons (and possibly positrons) from a synchrotron-cooled distribution, with a power law of roughly the index observed. It could also explain the observed Xray emission. However, since the power-law index produced by Fermi acceleration is a strong function of the compression ratio one would need some fine tuning to explain 2 3 For a definition of this term see Appendix B.1.1 For a short review on Fermi acceleration see Kirk 1994, for example. 73 the observed constancy of the radio–to–optical spectral index, which does not equal the limiting value for a strong adiabatic shock. Furthermore, there does not seem to be a significant amount of cooling between the knots even at the highest optical frequencies observed, which would be expected for the assumed B -fields and interknot distances. (2) Particles could be transported in a loss-free channel in the interior of the jet, with the bulk of the emission produced in a thin outer layer of high magnetic field strength (Owen et al. 1989). In this picture, the knots and filaments would be interpreted as instabilities with greatly increased magnetic field strength wrapped around the jet. The emission would then be fed by particles from this channel. The radio brightness profiles across the jet seem to suggest a limb-brightened emission, but a reinvestigation of the HST observations (SBM) shows that the optical emission is more concentrated to the inner regions of the jet. Also, a new radio volume emissivity map by SBM (see Figure 3.4), produced by deconvolving a processed 2 cm VLA image of the jet, places the brightest spots in the jet interior. This argues against a field-free zone in the jet interior. (3) On–the–spot reacceleration by a yet unknown process could maintain the cut-off particle momentum at the observed level, as has been proposed by Meisenheimer et al. (1996) in a model similar to ours (see x3.4.2). This has the advantage of explaining all the observed features, but invokes unknown physics to explain the apparent lack of cooling. 3.1.2 Proposed Solution Inspired by the observed correlation between the emissivity variations and the cut-off frequency, by the newly deconvolved volume emissivity (SBM), and by the new evidence for relativistic bulk velocities (Stiavelli et al. 1997; Biretta et al. 1995, 1999), we propose a simple way of explaining the observations. The only standard assumption we give up is the assumption of equipartition, which does not seem to have a very firm physical foundation anyway. Magnetic 74 fields smaller than equipartition by a factor of 1:5 in excess of 2 3, coupled with bulk Lorentz factors 3, can readily explain the lack of strong synchrotron cooling. jet In our model the fluctuations in the cutoff frequency are produced by weak shocks, so that the influence of the compressions on the plasma distribution function can be considered to be adiabatic4 . As a result, we are able to explain the general behavior of the cutoff reasonably well; the magnetic fields we derive from our own fits to the data are below equipartition with a convincing level of confidence, but the inferred total pressures do not necessarily need to exceed the equipartition values. Additionally, for relativistic jets the equipartition values for B -field and pressure are less than in the nonrelativistic limit, so the pressures we derive can fall below the equipartition value in the nonrelativistic case. The importance of this model therefore lies in its ability to explain the observations of the jet (i.e., the lack of cooling and the amplitude of the fluctuations in emissivity and cutoff frequency) in a self consistent fashion without invoking unknown physics. Since independent determination of magnetic fields in optically thin synchrotron emitting environments is otherwise impossible, this method provides a unique opportunity to learn more about the physical conditions in extragalactic jets. The fact that our model requires relativistic effects to be at work is a further step in the chain of evidence for relativistic bulk velocities of the jet plasma in large scale radio jets. This chapter is organized as follows. In x 3.2 we present a nonrelativistic treatment of the synchrotron emissivity, taking into account cooling and assuming that the particles and fields respond adiabatically to changes in the flow density. Once relativistic effects are incorporated into the treatment in x 3.3, we use the data of SBM and M99 to constrain the magnetic field strength of the jet. Chapter 3.4 discusses confinement and stability of the jet in the light of x 3.3, the production of X-ray emission in knot A, polarization, and limits on the particle acceleration site; and x 3.5 gives a brief summary of the pressures derived from the results of 4 The energy of the accelerated particle is proportional to its initial energy and the compression ratio of the plasma to the 4=3 power. Thus, if multiple species or populations of particles exist in the plasma, the fraction of internal energy in each species remains constant throughout the acceleration. 75 the results and future prospects. The Appendix gives a brief review of major properties of synchrotron radiation, shows the solution to equation (3.4) explicitly, and comments on the fitting procedure by M99. 3.2 Adiabatic Effects on Synchrotron Emission Our model rests on the hypothesis that Fermi acceleration is unnecessary to explain the fluctuations of radio–to–optical emissivity and cutoff frequency along the M87 jet3 . Given certain assumptions about the orientation and degree of disorder in the magnetic field, and the degree of anisotropy permitted in the relativistic electron distribution, we can relate changes in both the emissivity and the cutoff frequency uniquely to changes in the density of the jet fluid. These adiabatic effects are readily combined with the effects of synchrotron cooling (Coleman and Bicknell 1988). In effect, given the emissivity map of SBM, we can predict the run of the cutoff frequency along the jet, and vice-versa. Since we also have M99’s observations of the cutoff frequency as a function of position, our adiabatic model is subject to a powerful self-consistency check. Observationally, the main changes in emissivity and cutoff frequency are rather localized, and associated with the positions of the knots. These small-scale fluctuations therefore provide the strongest check on our assumption of adiabaticity. The large-scale trends then determine the best fit to the magnetic field strength. We have already seen that the apparent lack of a large-scale synchrotron cooling trend is incompatible with a magnetic field strength as large as the mean equipartition value (see Fig. 3.5). Neglecting relativistic and projection effects, it would require a magnetic field as low as 25 G to obtain a cooling length of 2 kpc at optical frequencies. This is an order of magnitude smaller than the mean equipartition field and would require a total (particle + magnetic) pressure of 1:2 10 7 dyn cm 2 to produce the observed average amount of synchrotron emission, compared to an equipartition value of 4:0 10 9 dyn cm 2. As noted earlier, the physical basis of equipartition is weak. Estimates of B -fields in 76 radio hot spots based on the synchrotron cooling time indicate that in some cases equipartition might be correct up to a factor of 2 (Meisenheimer et al. 1989), but the conditions in the jet might very well be different from those in the lobes. We are therefore free to consider the magnetic field strength to be a free parameter. Applying our adiabatic model to the observational data, we can derive an estimate for the magnetic field strength. In the case of the M87 jet, this estimate lies below equipartition, even when relativistic effects are taken into account (x 3.3). Our model for the evolution of the particle distribution function follows that of Coleman and Bicknell (1988). We assume that pitch angle scattering due to plasma micro–instabilities keeps the particles close to an isotropic distribution in the fluid rest frame. In the absence of cooling, this would imply that the relativistic electrons respond to compressions like a adiabatic = 4=3 (i.e., ultrarelativistic) fluid, but this behavior will be modified by synchrotron cooling. Because the magnetic field is frozen into the plasma, its strength should change as the plasma density fluctuates along the jet. Depending on the orientation and the degree of disorder of the field, its variation will depend roughly on the density change to some power : B (r) / %(r) , where % is the proper particle density and r is the distance from the core. For a completely disordered magnetic field, = 2 , whereas for a homogeneous field the power depends on the orientation of the field with 3 respect to the compression normal, with = 1 for an orthogonal orientation, = 0 for parallel orientation. Since the polarization of the jet is of order 10%-20% in the interknot regions, compared to the maximum polarization of 70% for a homogeneous field, it is likely that the magnetic field has a disordered component, so it is reasonable to assume to be of order 23 (but see x3.4.4). The ordered B -component is aligned with the jet axis almost everywhere except in the brightest knots, as can be seen from polarization measurements (Biretta 1993). We do not know its orientation with respect to the compression normal, because the orientations of the (presumably oblique: see BB) shocks are unknown. However, our results are not very sensitive to what the actual value of is, as we will show later. We therefore make the simplifying assumption of a single exponent describing the field variations. Using the scaling relation for 77 the synchrotron emissivity of a power law momentum distribution f (p) d3 p N0 p a d3 p = N0 p 4 (corresponding to a spectral index of = a+2 dp; (3.1) a 3 ) under adiabatic compression (e.g., Coleman 2 and Bicknell 1988, see equation [B.5]): 2+3 j / (B sin #)1+ % 3 ; (3.2) where # is the angle between magnetic field and line of sight, we can express the field relative to its value at r0 = 000 :5, the (arbitrary) injection point at which we start the calculation, as a function of the emissivity ratio j=j (r0 ): B = B (r0 )(j=j (r0 )) where (3.3) [1 + + (2 + 3)=(3 )] 1 . A necessary condition for this approach to be valid (in addition to the assumed isotropy and the absence of Fermi acceleration) is the assumed steadystate injection of relativistic particles and fields by the central engine, which allows us to relate densities and fields at each r to the corresponding values at the injection point r0 at a given instant of time. Is it plausible to neglect Fermi acceleration in the shocks that comprise the knots? Except for knot A, the brightness changes along the jet are moderate. In knot A, the brightest feature, the emissivity changes by a factor of order 10 (SBM), which, if entirely due to a sud- den compression of the plasma, can be produced by a proper compression ratio of r measured in the respective rest frames of the plasma if we take infer smaller density contrasts, r 1:5. = 2:7 as 2 3 . For the other knots we Consistent with this observation, we will henceforth take the knots to be weak shocks, in accordance with the suggestion by BB that the knots are highly oblique (and therefore weak) shocks. Thus, because Fermi acceleration leaves the spectral index unchanged if the shock is weak enough, we will henceforth neglect its effect on the cutoff frequency. Section 3.4 discusses Fermi acceleration in more detail, with particular focus on the possibility of Fermi acceleration occurring in knot A. 78 Furthermore, because the shocks are believed to be oblique, we take the fluid velocity to be constant to first order, both in magnitude and direction. For the shock jump conditions in the non–relativistic limit (which we consider in this section) the velocity component perpendicular to the shock plane v? is inversely proportional to the density, thus for a proper compression ratio of 2:7, as seen in knot A, the perpendicular velocity component should change by a factor of 0:37. For highly oblique shocks, v? is small compared to vk and the velocity will not change significantly. Moderate changes in velocity would be easy to incorporate in principle; yet with our current ignorance of the velocity field and shock parameters, such a level of detail is unwarranted. We will comment on the validity of this assumption in x 3.3. We also postpone a treatment of the motion of the knots until x 3.3, and assume them to be stationary for the rest of this section. With these assumptions we are ready to calculate the downstream cutoff frequency for a given initial cutoff momentum in the injected particle distribution and a given B -field at r0 . We use the transport equation as presented by Coleman and Bicknell (1988): df 1 d% @f @ + p = Ap 2 (p4 f ) dt 3% dt @p @p written in the rest frame of the fluid. Here, A= (3.4) f = f (p) is the electron distribution function and 4e4 2 9m4e c6 B is the synchrotron loss term. The equation is valid for the assumed case of isotropy and negligible Compton losses (for a brief discussion of Compton losses see x 3.4.1). The solution of this equation is 0 1 14 3 p % f (p(r)) = f0 (p0 ) @ 0 1 A p %3 (3.5) 0 where f0 is the injected momentum distribution and 1 (%=%0 ) 3 p0 p(r) = R t(r) 1 (1 + p0 t(r0 ) A(t0 )(%(t0 )=%0 ) 3 dt0 ) (3.6) (see Coleman and Bicknell 1988 and Appendix B.2) where the subscript 0 denotes the values at injection point r0 . Even for arbitrarily large p0 , p(t 6= 0) can only reach a limiting value of pmax (t) (%=%0 )1=3 1 0 0 0 t(r0 ) A(t )(%(t )=%0 ) 3 dt R t(r) (3.7) 79 10-2 j(2cm) [Jy/pixel3] 10-3 10-4 10-5 10-6 10-7 10-8 200 400 600 800 1000 pixel Figure 3.4: Emissivity map provided by SBM (top panel), produced by symmetrifying the 2cm VLA map of the jet. The scaling is logarithmic in Jy/pixel3 for 0:00 0223 pixels. The bottom panel shows a slice along the jet axis to demonstrate the scaling of the emissivity as a function of distance from the core (solid line) and the emissivity averaged across the jet (thick line). Note that the variations along the central slice are much higher than for the averaged j . This is very likely due to the fact that the deprojection method is least accurate towards the jet axis. Thus, any momentum distribution subject to synchrotron cooling without replenishment of high energy particles must develop a cutoff at high energies. Equation (3.6) describes how the momentum of a given particle changes along a streamline. Thus, if the distribution initially cuts off at pc;0 , we can calculate the cutoff momentum 1 pc (r) downstream. Because in our model the density %(r) is proportional to B (r) and because we know the scaling of B with r from equation (3.3), we can eliminate % and B=B0 from equation (3.6). The remaining parameters are B0 , pc;0 , and j (r )=j0 , the latter being provided by the Sparks et al. data, shown in Figure 3.4. The cutoff momentum pc is related to the observed cutoff frequency c by the expression c = 3e 2 p B sin #: 4m3e c3 c (3.8) Equation (3.8) contains another parameter, #, the angle between the line of sight and the mag- 80 netic field. For now we shall set the factor sin # 1, which is valid for disordered fields, since 1) the regions in which the field is perpendicular to the line of sight have the highest emissivity, and 2) assuming randomly oriented fields, half of the field orientations lie in the range from 60Æ to 90Æ to the line of sight, i.e., sin # 0:866. Thus the cutoff frequency is mainly determined by field orientations close to 90Æ or sin # 1. We can now determine the free parameters B0 and pc;0 by applying a least chi-squared method to fit the observed cutoff frequency c;obs with the value determined from equations (3.6) and (3.8), using the emissivity map j (r )=j0 provided by SBM. We prefer to average the emissivity across the jet (we averaged j over a disk with jet diameter at every location along the jet), which minimizes small scale variations probably due to the deprojection procedure, which is most unreliable towards the jet axis (we will comment on the possible uncertainty introduced by this step in x3.3). Because M99 also averaged across the jet, this seems to be the most appropriate way of calculating the cutoff frequency. Figure 3.5 (calculated for a bulk Lorentz factor of jet = 1:1, a radio spectral index of R = 0:5, LOS = 90Æ , and = 2 3 ) shows the observed cutoff frequency c;obs (vertical bars) with error bars and the best fit curve (solid line), which seems to reproduce the scaling of the cutoff frequency reasonably well. (The radio spectral index seems to break to 0:65 at 10 GHz, so we have used both = 0:5 and 0:65 in our fits with insignificant differences in the average parameters but smaller chi-squared for 0:65; see x3.3.) equipartition For comparison the plot also shows the best fit cutoff frequency for B -fields (dashed line). The mean B -field is of order 10 G, even smaller than the zeroth order estimate made at the beginning of this section. Assuming (arbitrarily) a lower cutoff at = 107 Hz and the observed high-frequency cutoff at 1015 Hz yields an average total pressure of value of p 8 10 8 dyn cm 3 10 9 dyn cm 2 for the given parameters, compared to an equipartition 2 . In calculating absolute values for both pressure and B- field, projection (i.e., foreshortening and length scale) effects must be taken into account, since the emissivity was derived for a side-on view of the jet. This introduces a factor of in intrinsic emissivity and pressure for a given magnetic field and a factor of sin LOS 4 (sin LOS ) 7 in 81 1016 νcutoff [Hz] 1015 1014 1013 1012 0 5 10 15 distance in arcsec 20 Figure 3.5: Measured cutoff frequency along the jet from M99 (vertical lines with error bars). Solid line: best fit curve as calculated from the emissivity measured by SBM for jet = 1:1, = 23 , and LOS = 90Æ ; dashed line: best fit curve for the case of equipartition calculated from SBM data for the same set of parameters. equipartition pressure. It seems that the proposed modest compressions can account for the fluctuations seen in the spectral cutoff, and the large scale decrease in c is well reproduced. It would be helpful to determine both the emissivity and the spectral index maps from the same method and data, thus eliminating errors due to different reduction procedures. We comment on the deviations and uncertainties in this fit in x 3.3. It is important to note that this technique should be independent of what the actual shape of the particle distribution is, because it simply tracks the behavior of a single feature in the spectrum, which could be identified with either a break or a cutoff. As seen in this section, one runs into problems with the jet pressure for nonrelativistic bulk velocities. Also, the observed mildly relativistic proper motion of the knots and the jet’s onesidedness favor a relativistic interpretation, as do the knot spacing and morphology (BB). The results indicate that Lorentz factors of order 2 5 fit the observations best. In the next section we will investigate the effects of these suggested relativistic bulk velocities. 82 3.3 Relativistic Effects Relativistic motions not only explain the onesidedness of the M87 jet, but also help to solve the synchrotron cooling problem mentioned in the introduction. The travel time in the electron rest frame is reduced by a factor jet due to time dilation, the intrinsic emissivity is reduced by a factor D2+ (where D is the Doppler factor D=[ jet (1 and the intrinsic cutoff frequency is Doppler shifted downward by a factor cos LOS )] D. 1 ), As a result, the apparent synchrotron lifetime can be a significant underestimate of the intrinsic value. Biretta (1993) estimates the lower limit on the jet–to–counterjet radio brightness ratio to 150 380 (the higher value corresponds to the assumption that jet and counterjet have identical appearance). Based on this limit we adopt line–of–sight angles 35Æ and Lorentz factors 2. Note that even Doppler factors smaller than unity can lead to a large jet–to– be counterjet brightness ratio, as the counterjet brightness is severely reduced for large jet . We repeat the analysis of x 3.2 using the emissivity profile of SBM, this time corrected for Doppler boosting and projection effects. Again, for fitting the cutoff frequency only emissivity ratios are important, so these corrections do not change the fitting procedure as long as changes in the bulk velocity can be neglected. We are confident that at least the direction of the flow is not changed significantly before knot C. The only knot for which such effects could be important is knot A, because it displays a jump in emissivity of 11, whereas in the other knots the emissivity is increased by a factor of order 3 only, which implies very moderate compressions. Using the relativistic continuity equation for an oblique shock we have estimated the post–knot A Lorentz factor to be jet;A+ 3 for a pre–knot A jet;A = 5, a compression ratio of 3 and intrinsic obliquities 60Æ . Although the change in jet might seem large at first glance, the impact such a velocity change in the shock at knot A as on our fits is not large, as we will explain below. We modify equation (3.4) to follow the electron distribution in the fluid rest frame by replacing t with d with d , where and dt d is the proper time. The same changes apply to equation (3.6). Strictly speaking, the fluid frame is not an inertial frame and we would have to include 83 accelerational terms into the equation, introducing an anisotropy. But our assumption should be adequate, provided that isotropization takes place over short enough scales. Treating the response of the distribution function to compressions as adiabatic and assuming isotropy (i.e., an adiabatic index of 43 ) we calculate the changes in B and cutoff mo- mentum (measured in the fluid frame) from the emissivity changes in the fluid frame. The substitution t ! takes care of the time dilation effects. In order to incorporate the observed motion of the knots, we must correct A( 0 ) and %( 0 ) in equation (3.6) for light travel time effects between the source and the observer. This is because the knots move during the time it takes a particle to travel from r0 to r . We need to know the ratios B=B0 and %=%0 experienced by a particle as a function of proper time 0 in order to be able to do the integration in equation (3.6). Because we infer the relative values of B and % at a given position from the emissivity ratio j (ruid )=j0 , it is important to know the velocity of the emissivity pattern. We assume that the pattern of density and field fluctuations retains its shape and moves along the jet at a fixed speed vpattern , taken to be smaller than vuid and set equal to 0:55 c everywhere in our calculations for simplicity. If the present field distribution (i.e., at a given time t = 0 in our frame, corrected for light travel time effects) is expressed by B (r), then the field at time t0 and position r 0 is given by B (r 0 + vpattern t0 ). Now, for a particle currently at r , the equation of motion is r0 = r by the particle as a function of time is vuid t0 . B [r Therefore, the field distribution experienced (vuid vpattern )t0 ]. Appropriate modifications to equation (3.6) are straightforward. The effect of the pattern speed on the result is not very dramatic, reducing 2min by about 6%. With this set of assumptions we can once again proceed to integrate the modified equation (3.6) for various LOS and jet . Using a minimum chi-square routine we can determine the best–fit values for B0 , and p0 . Relation (3.3) then yields B (r ). Figure 3.6 shows a typical chi-square plot calculated for jet = 2 . The equipartition value for the average 3 = 3, LOS = 25Æ , and B -field is shown as a shaded area at 89 G. 84 1.6 1.4 equipartition B-field P0 × 1010[g cm sec-1] 1.8 4 1 1.2 3 2 5 1.0 0.8 20 40 60 Bmean[µG] 80 Figure 3.6: Contour plot of the 2 values as a function of Bmean and the injection cutoff momentum P0 for = 25Æ and jet = 3:0. Shown are the contours corresponding to a reduced 2 of 45 and integer multiples of this value. The shaded line on the right of the plot shows the equipartition B -field for this set of parameters. The upper limit on Bmean , set by 22min contours, lies at 49 G, 75% above the best fit value, Bmean = 28 G. The lower limit set by The average equipartition field of Bmean 22min is 5 G, 80% below the best fit value. 89 G lies above even the 52min contour. The lower limit on B is not nearly as strict, due to the fact that cooling is not dominant, i.e., we can produce a similar spectral behavior by reducing the magnetic field and increasing the particle energy, which produces the tear-shaped appearance of the contours. Thus, strictly speaking, the best fit values for the B -field should be regarded as upper limits. The reduced 2min values (i.e., 2min divided by the number of degrees of freedom) fall above 44, which is uncomfortably high. However, because we do not have formal errors for the emissivity deprojection by SBM, which will introduce a significant uncertainty, a high value for 2min is not all that discouraging. Estimating the average uncertainty in the emissivity by comparing the averaged emissivity to that derived from taking only a slice along the jet yields an uncertainty of order 50%, which leads to uncertainties in the predicted cutoff frequency of 85 roughly 20%. This is significantly higher than the formal error in M99’s data and will reduce the 2min by a factor of approximately 10. The 2min values are dominated by the region beyond knot A. The post–knot A residuals in our fit are not larger than the residuals in the pre–knot–A region, but because the post knot A region is brighter, the error bars on the measured cutoff frequency are smaller, which increases the 2min . The deprojection procedure, which assumed an axially symmetric flow, breaks down beyond knot A, which will introduce significant uncertainty. Also, non–uniformities in the emissivity could lead to large errors if the optical emission peaks at different locations than does the radio emission. Field orientation effects and changes in jet and LOS might also contribute to the error. We performed the same procedure just out to knot A and found that, with the same parameters, the reduced 2min shrinks to 13. Leaving B and pc as free parameters reduces 2min to 10, but also reduces the B -field significantly. Because in this case the algorithm mainly fits the region around knot A (where the error bars are smallest), we cannot expect the global run of c to have significant impact on the fit, which would be necessary to extract information about the average magnetic field. We conclude that the reproduction of fine detail is not satisfactory in the region beyond knot A. However, the gross run of c , which is principally responsible for constraining our parameters, is reasonably well reproduced. The best–fit average magnetic field Bmean , as a function of jet and LOS , is plotted in Figure 3.7. Figure 3.8 shows the average ratio hB=Beq i1 as a function of jet for LOS = 15Æ to 30Æ in increments of 5Æ , and the area corresponding to the limiting jet–to–counterjet brightness ratio of 150 - 380. Note that the equipartition magnetic field has to be corrected by a factor of 2+ 1 D 3+ (sin LOS ) 3+ for projection and Doppler boosting of the emissivity; this has already been taken into account in the figure. Clearly, for jet in the range 3 5 and LOS < 25Æ the departure from equipartition is not very large (roughly a factor of 0:2 < hB=Beq i < 0:6). In order to test the dependence of the best fit B0 on the parameter the same curves for = 1 and = B1 B2 from the 1 B1 = we have calculated 1 15 . Figure 3.9 shows the fractional deviation 2 curve for models with 3 15Æ LOS 30Æ . B B The deviation is small 86 45 Bmean [µG] 40 35 30 brightness ratio limit 15˚ 20˚ 25˚ 30˚ 25 20 15 2 3 4 5 Γjet 6 7 8 Figure 3.7: B -field averaged along th jet between 000 :5 and 2200 as a function of jet for LOS = 15Æ (solid line), LOS = 20Æ (dotted line), LOS = 25Æ (dashed line), and LOS = 30Æ (dasheddotted). The grey region indicates the jet–to–counterjet brightness ratio limit of 150 (dashed grey boundary) - 380 (solid grey boundary, Biretta 1993). 0.70 brightness ratio limit 15˚ 20˚ 25˚ 30˚ 〈 B / Bequipartition 〉 0.60 0.50 0.40 0.30 0.20 2 3 4 5 Γjet 6 7 8 Figure 3.8: Ratio of the best–fit B -field to the respective equipartition B -field Beq averaged between 000 :5 and 2200 for = 23 as a function of jet . The different values of LOS are labeled similarly to Fig. (3.7). The grey region shows the jet–to–counterjet brightness limit (dashed grey boundary: 150, solid grey boundary: 380). 87 Γjet,AΓjet,A+ ζ = 1 / 15 ζ=1 α2cm= 0.65 (∆B/B)ζ,Γ,α 0.20 0.15 0.10 0.05 0.00 2 3 4 5 Γjet 6 7 8 Figure 3.9: Fractional deviation BB of the best fit B -field (averaged between 000 :5 and 2200 ) jB1 B2 j , where = 2 and either = 1 for a. two different values of : BB 1 2 B1 3 15 (hatched, solid boundary) or 2 = 1(hatched, dotted boundary); b. a uniform jet, compared to Bbreak j , where B jBuniform a jet slowing down at knot A: BB break is the best fit average Buniform B -field for a jet slowing down from jet;A to jet;A+ at knot A, and Buniform is the best fit average field for a uniform jet with jet = jet;A (dark grey region, short dashed boundary) The latter is plotted versus and jet = jet;A+ (light grey region, long dashed boundary). jB1 B2 j for our standard B jet;A+ ; c. two different 2cm radio spectral indices: B B1 value 1 = 0:5 and 2 = 0:65, shown as the black area. (The width of the band corresponds to LOS between 15Æ and 30Æ in each case.) compared to the expected errors introduced by the simplifications we made and to the range in B allowed by our minimum chi-square procedure, at most 12% for 2 = 1 15 and small jet . This is not a very reasonable value for in any case, because the field has a random component, thus should be higher, and the probability of the field being in the shock plane (thus having = 1) is twice as high as for the field being normal to the shock. We conclude that our ignorance of the precise behavior of B under compression is not a serious obstacle to the application of our model. We also tested the impact a change in jet at knot A might have on our results. As we mentioned earlier, the best fit B -field values we derive are upper limits. This is the reason why 88 a change in jet at knot A does not change our results significantly: generally, lower Lorentz factors require lower fields to explain the observed lack of cooling. If the jet is slowed down beyond knot A, we will need lower average fields to fit this region. However, lowering the field does not change the quality of the fit much (the 2 is essentially unchanged), so the global field strength is simply set by the region with the lower Lorentz factor, jet;A+ (the relative scaling of B is still determined from equation 3.3, taking relativistic beaming into account). We have introduced by hand a change of jet at knot A into our model (we solved the continuity equation at the shock, assuming an obliquity of 60Æ , for the velocity change that would reproduce the observed emissivity jump of 11, including relativistic beaming and adiabatic compression), and calculated the fractional deviation BB Bbreak j of the derived averaged B -field. jBuniform Buniform Here, Buniform is the best fit average B -field derived for uniform jet and Bbreak is the best fit field for a jet slowing down from jet;A to jet;A+ at knot A. Figure 3.9 shows BB for uniform jet models with jet set to either jet;A or jet;A+ (filled light and dark grey regions, respectively). The latter is always less than 18% for the parameter range we used. Note that for post–knot–A jet;A+ ’s above 5, the pre–knot–A jet;A exceeds 8.5, thus jet;A+ > 7 can be ruled out on the basis of gross energy balance arguments (see next section). For completeness we have shown the deviation of the best fit average B -field BB jB1 B2 j for a 2 cm radio spectral index of = 0:65 instead of = 0:5 as the black region 2 1 B1 in Figure 3.9. One can see that the difference is negligible compared to other uncertainties. 3.4 Discussion In the preceding sections, we have demonstrated that a) magnetic fields slightly below equipartition and b) moderately relativistic effects are able to explain the general behavior of the spectrum in M87. In this section we will examine the confinement properties of the jet and compare our model with a previous model by Meisenheimer et al. (1996). We will also comment on the production of X-ray emission in knot A, and on the consistency of our model with polarization measurements, and we will estimate the minimum distance from the core at 89 which particle acceleration must occur. 3.4.1 Confinement Naturally the question arises whether the jet can be confined under the conditions we proposed above. The usual assumption for a jet to be confined is that it is in pressure equilibrium with its surroundings. Alternatively, one could imagine the jet to be freely expanding into an underpressured surrounding medium. BB argue that in order to produce shocks via Kelvin-Helmholtz instability, some interaction between jet and surrounding medium has to take place, as opposed to a free expansion scenario. They also show that the minimum Lorentz factor jet for a freely expanding jet with no cold matter content is at least 13, much higher than the values we have used above. Because we would most certainly fall out of the beaming cone for such a high jet jet, the intrinsic emissivity would be much higher than the observed value. As BB point out, the energy flux of the jet would far exceed the estimates made on the basis of the expanding bubble the M87 jet blows into the ISM. A jet that high would also raise questions about the location at which the jet is decelerated to nonrelativistic velocities, and seems inconsistent with the claimed detection of IR counterjet emission by Stiavelli et al. (1997). We can therefore rule out the picture of a freely expanding jet. As a consequence we need a mechanism to provide confinement, i.e., we need to set the jet pressure in relation to the ambient pressure. The ambient gas pressure in the center of M87 has been derived by White and Sarazin (1988) from fitting cooling flow models to the Einstein X-ray observations. The values they find fall into the range pISM = 1 10 10 dyn cm 2 to p ISM = 4 10 10 dyn cm 2 . It is important to note that the pressure of the interstellar medium in M87 might not be representative of the pressure of the immediate environment of the jet. In fact, BB’s analysis of the helical KelvinHelmholtz instability leads to the conclusion that the ambient medium of the jet is significantly overpressured with respect to the interstellar medium in M87. Note also that the pressure in the knots might well exceed the ambient pressure without losing confinement, as long as the pmean [dyn cm-2] 90 90˚ non relativistic equipartition pressure brightness ratio limit 15˚ 20˚ 25˚ 30˚ 10-8 10-9 ISM pressure ISM pressure 2 3 4 5 Γjet 6 7 8 Figure 3.10: Total pressure pmean averaged along the jet between 000 :5 and 2200 as a function of jet . Labels according to Fig. (3.7). For comparison, the dashed-triple-dotted line shows the equipartition pressure for a non-relativistic jet seen edge on (i.e., LOS = 90Æ ). The hatched area shows the estimated ISM pressure (White and Sarazin 1988) in M87. average pressure does not. We have calculated the average total pressure pmean in the jet from the averaged emissivity and the best–fit B -field for various angles and Lorentz factors, as shown in Figure 3.10. The assumptions we have made in constructing this plot are analogous to those of SBM, who (arbitrarily) assumed a lower cutoff at 107 Hz, a high energy cutoff at 1015 Hz, a spectral index of RO = 0:5, and equipartition between heavy–particle and electron energy. the spectrum is steeper than R (Note: because = 0:5 above 10 GHz, our estimate of the pressure is likely to be an overestimate.) We have also assumed isotropic emission in the plasma rest frame by using an average value of # = 54Æ for the term sin1+ # in the emissivity equation (3.2). For comparison we have also calculated the equipartition pressure and plotted the ratio of pressure to equipartition pressure in Figure 3.11. It is obvious that we are far above equipartition for small values of jet and large LOS , but as we approach the favored range of and LOS < 30Æ , ptotal jet 3 approaches the equipartition value. The exact value of the pressure 91 brightness ratio limit 15˚ 20˚ 25˚ 30˚ 〈 p / pequipartition 〉 4 3 2 1 2 3 4 5 Γjet 6 7 8 Figure 3.11: The ratio of the best–fit particle pressure to the respective equipartition value averaged along the jet as a function of jet . Labels according to Fig. (3.7). depends critically on the details we put into the model spectrum. For a jet composed entirely of electrons and positrons, the pressure would go down by a factor of 12 , whereas the equipartition 4 pressure would only decrease by a factor of ( 21 ) 7 = 0:67. The lack of information about the low–frequency spectrum inhibits any statements about the low–energy particle distribution. However, it is safe to assume that the power law does not continue down to non-relativistic energies. It is obvious that a magnetic field far below equipartition alone cannot explain the behavior of the jet — it might account for the spectral changes but it requires the pressure to be much higher than that of the surrounding medium. Field orientations close to the line of sight will lead to an underestimate in emissivity, pressure, and intrinsic cutoff frequency and will require even lower magnetic fields and even higher pressures in order to prevent significant cooling. This changes as we increase jet : the inferred pressures are close to the value for the interstellar medium in M87 as derived by White and Sarazin (1988), for jet 3 5 and LOS < 25Æ . This, combined with the possible overpressure of the jet’s immediate environment relative to 92 the ISM, leads to the conclusion that there is no confinement problem. For small values of the magnetic field, one might ask if inverse Compton losses become dominant. A simple order of magnitude estimate shows that this is not the case. The ratio of synchrotron to inverse Compton loss timescales is equal to the ratio of photon energy density to magnetic field energy density (Rybicki and Lightman 1979). The magnetic field strength has been estimated above. To derive an estimate of the photon energy density produced by the synchrotron emission, we normalize to the radio luminosity corrected for beaming and projection effects and integrate over an RO = 0:65 radio–to–optical power law that cuts off at 1015 Hz. This shows that the inverse Compton lifetime due to just the synchrotron radiation field of the jet is roughly an order of magnitude longer than the synchrotron lifetime for the parameter range we suggested above. The starlight background at the center of M87 also contributes to the photon energy density. Using an isothermal sphere profile, normalized to the total luminosity of M87, we arrive at a central photon energy density roughly an order of magnitude smaller than that of the magnetic field, small enough to justify the assumption of negligible Compton losses. 3.4.2 Comparison with Earlier Models It is instructive to compare our model to an earlier ad-hoc model by Meisenheimer et al. (1996, see also Biretta 1993), which bears a lot of similarity to our model. They start from the same assumption that the spectral changes along the jet can be explained by simple compressions and assume that the cutoff momentum c is almost constant along the jet, parameterizing it as a function only of the transverse jet radius (measured from the 2 cm radio map): c /R 1 3 2 — note that for an adiabatic compression of the plasma transverse to the flow c goes as R 3 . They take the B -field to consist predominantly of a toroidal component, B , and hold the poloidal component Bz fixed. They determine the longitudinal compression ratio of B and of the particle density n from their fit to the cutoff frequency c with equation 3.8. However, in 1 an adiabatic compression, the cutoff momentum varies as n 3 and will therefore be affected by longitudinal compressions as well (here is where our assumption of a disordered field allows 93 us to determine a relation between density and magnetic field, so we can solve equation 3.8 uniquely for B ). They neglect the fact that the synchrotron emissivity is enhanced in adiabatic 2 compressions by n1+ 3 B 1+ (equation 3.2) rather than n B 1+. Since the shocks might well be oblique, their assumptions that B scales as the longitudinal compression ratio and that Bz is constant might also not be valid. Meisenheimer et al. (1996) favor an intrinsically onesided, subrelativistic jet, viewed close to perpendicular (LOS 90Æ ). Knot A would be a head–on shock in this scenario. As we have mentioned above, for this set of parameters additional acceleration has to be provided to maintain the optical emission out to large distances from the core. Meisenheimer et al. (1996) favor an unknown global acceleration process to explain the constancy of the cutoff momentum. With these assumptions, their model yields similar results to ours in that it reproduces the small scale brightness variations on the basis of the changes in cutoff frequency. Our model could thus be regarded as an extension of their approach, putting it on the theoretical basis of adiabatic compressions, with a different mechanism for providing the large scale constancy of the spectrum. 3.4.3 X-ray Emission An important result from the analysis above is that cooling longward of UV energies is not important over the length of the jet — the proper time is reduced by a significant factor and the magnetic fields are small enough to leave the spectral shape unchanged. This conclusion begs the question of the origin of the X-ray emission detected by the Einstein Observatory and ROSAT. Both observations show emission from the core/knot D region and knot A. 3.4.3.1 The Role of Particle Advection: Ultra-high-energy particles, capable of radiating in the X-ray regime, could be carried out from knot D, where X-ray emission is observed, to knot A, and reaccelerated in the shock by the adiabatic compression mechanism discussed above. For this to happen the spectrum 94 would have to break rather than cut off in the optical. The presence of a break instead of a cutoff would not change our fits, as long as the break is located above the frequency we fitted. We have calculated the behavior of particles with X-ray emitting energies along the jet and found that for our best fit at B -fields cooling out to knot A will have produced a spectral cutoff 1017 Hz – which is where most of the Einstein HRI’s sensitivity lies. Since the B -fields we derived are upper limits, a lower field could leave the distribution function unchanged even at such high energies. Therefore this mechanism of producing X–rays is marginally consistent with our model. It might also account for at least part of the X–rays. Note that, as suggested by various authors (e.g., Biretta and Meisenheimer 1993), the X-ray emission could also be of non–synchrotron origin altogether. 3.4.3.2 Fermi Acceleration at Knot A: The compression of a factor 3 inferred from the analysis above indicates that Fermi acceleration might be present in knot A, although the moderate change in emissivity and the constancy in radio and optical spectral index suggests that it might not be very efficient. It is possible that Fermi acceleration occurs at parts of the shock only, resulting in a particle distribution composed of a compressed and a Fermi-accelerated preshock distribution. In order for Fermi acceleration to take place at all the shock has to be subluminal, i.e., the intersection point of a given magnetic field line and the shock front has to move with a speed smaller than the speed of light, in which case we can find a frame in which the magnetic field is perpendicular to the shock front. This is the case for fields not too closely aligned with the shock plane. In the nonrelativistic case the field orientations leading to a superluminal shock are rare, and subluminal shocks are the rule rather than the exception, so one would expect Fermi acceleration to take place. Because in relativistic shocks the percentage of superluminal field orientations rises sharply with shock , Fermi acceleration should become less important. In this limit, most of the particle acceleration would occur through the mechanism of “shock drift acceleration”. Begel- 95 man and Kirk (1990) presented a theory of this process valid in the relativistic case. They show that the adiabatic approximation is still accurate in the limit of p p < 1, where p is the up- stream Lorentz factor in the perpendicular shock frame and p the corresponding velocity. We have calculated this quantity for various obliquities and field orientations appropriate for knot A and it seems to fall into the desired range. For a disordered magnetic field we would have to average the resulting spectrum over all possible field orientations. The more superluminal the shock the less important would effects of Fermi acceleration be. Relativistic corrections to shock drift acceleration are only important for high p p , which, again, depends on the field orientation. Averaging over all possible field orientations would probably render these corrections unimportant. Fermi acceleration both changes the shape of an incoming power law spectrum and amplifies it. For an incoming electron spectrum of the form f (p) = A0 p a in the test particle limit (i.e., the pressure provided by the accelerated particles is negligible), and a nonrelativistic shock, the change of the spectrum depends on s 3r r 1 , where r is the compression ratio. If s < a the spectral index is changed to s. If s > a the slope remains unchanged but the spectrum is still amplified by a factor s s a (Kirk 1994). The radio spectral index is plying a 4 0:5 0:65, im- 4:3. To provide a boost in emissivity by a factor of 11, s has to be 5:1 5:5, implying a compression ratio of 2:2 2:5 (assuming = 2 ). Note that this is very close to 3 the compression ratio one derives for an adiabatic compression. The spectral index produced by such a shock is 1 1:25, consistent with the observed optical 1:2. Drury et al. (1982) showed that the produced power law softens as one departs from the test particle limit. Also, the simple treatment stated in this paragraph breaks down in the case of relativistic shocks, where the spectral index is no longer a simple function of the compression ratio. Recent investigations by Ballard and Heavens (1992) have shown that oblique relativistic shocks can produce rather steep spectra, but other results indicate that they might be more efficient in accelerating particles (i.e., producing flatter spectra) than their nonrelativistic counterparts (Kirk and Heavens 1989). SBM find an optical–to–X-ray spectral index of OX 1:4 96 for the knot A region, which seems to be consistent with low–efficiency acceleration. If Fermi acceleration were present at the shock and effective enough to change the spectral shape in the optical, it would no longer be feasible to use the data from the whole jet to determine the magnetic field. Rather, the same analysis could simply be carried out separately for the pre– and post–knot A regions of the jet. We would then have to make an estimate of the shock strength based on the known parameters in order to determine the ratio of pre– to post–shock Lorentz factor . Even in this case we would need Lorentz factors of order jet 3 to solve the cooling problem. However, based on the observed mild spectral changes, and the assumption that pitch angle scattering is strong, we conclude that Fermi acceleration, if present, will not be efficient enough at accelerating electrons to affect the spectrum below the cutoff. Inefficient Fermi acceleration might very well be present in knot A, producing the X-ray emitting particles observed. Prediction of the produced high–energy spectral index has to wait for more conclusive results on Fermi acceleration at relativistic oblique shocks. As is well known, shocks are more efficient at acceleration protons than electrons by a factor corresponding to the mass ratio of the two particle species. In order to explain efficient electron acceleration, an efficient energy transfer mechanism from protons to electrons is commonly invoked (Coulomb scattering is insufficient). Such a leap of faith is unnecessary in M87, as we have shown that no strong particle acceleration is needed to explain the observations. Slow energy transfer from protons to electrons can then be helpful in explaining the presence of high energy electrons and optical synchrotron emission in longer jets (such as 3C15). 3.4.4 Polarization An important complication to the treatment above is the fact that the magnetic field will not be completely disorganized — polarization measurements show that in some regions a homogeneous component is present. In fact, it is possible that cancellations between regions with homogeneous fields but different orientations occur along the line of sight (Meisenheimer 97 1992). In such a case, the assumption of disorganized fields, leading to justified. However, since the impact that the parameter 2 , is no longer 3 has on the fit is minor (Fig. 3.9), we feel this caveat is not very severe and merely mention this complication here. In addition to the unknown orientation of the jet itself, the field orientation is also unknown. Since synchrotron emission depends on the magnetic field orientation to the line of sight # as sin1+ #, it can be strongly peaked away from the field direction. The cutoff frequency also depends on sin #. Because the cutoff frequency is determined by sampling all regions along the line of sight, it is not obvious which value to choose for #. Fortunately, in a domain of disordered field the regions with the field oriented close to perpendicular will contribute most of the flux, thus the error we make by setting sin # to 1 will not be too large. Note that we used a value of # = 53Æ in calculating the pressure, the appropriate average of sin1:5 # over 4 steradian. Knot A shows a polarization of order 35% and a field orientation close to the shock plane. Neglecting relativistic effects, the small amount of upstream polarization, and the fact that shear might reduce the compression of the field, we can use the approximate formula (Hughes and Miller 1995) where + 1 (1 r 2 ) cos2 ; + 35 2 (1 r 2) cos2 is the fractional polarization, r is the proper compression ratio, (3.9) and is the line of sight angle from the shock plane, to obtain a lower limit on the compression ratio in knot A of r 2, valid for the inferred range of viewing angles with respect to the shock plane (BB). This is consistent with the compression ratios inferred above. Equation (3.9) also provides an upper limit of 35Æ on ; however, the shock is assumed to be oblique, so we cannot use this result to constrain LOS . 3.4.5 Particle Acceleration Radius Having an estimate of both magnetic field and cutoff momentum at the injection radius r0 , we can now try to determine where the actual particle acceleration has to occur. We assume 98 some radial dependence for the magnetic field in the inner portion of the jet (i.e., smaller than 0:500 ), for example a power law: B /r . Furthermore we make the simplifying assumption of a constant jet . By also taking B to be proportional to % , which determines the radial dependence of %, we can invert equation (3.6) and solve for the radius at which the cutoff momentum approaches infinity, in other words, the minimum radius inside of which acceleration has to occur: racc = r0 1 + 1 A r0 4p0 B02 e4 9 jet c7 m4e , and where A= A r0 ! 1. (3.10) 1 (2+ 31 ) 1 . The acceleration radius racc approaches zero if It is obvious that the estimate of racc depends critically on the value of . In Figure 3.12 we have plotted racc as a function of for LOS = 25Æ and jet = 3. In the same figure we have also plotted racc for the case in which B no longer scales like % — in this case we have taken % / r 2 and used the same values for LOS and jet (dashed line). If the jet expands at constant opening angle and with uniform jet , the decline of B with radius should correspond to 2, since the density scales like r 2 and dissipative effects will probably limit the rate of decline. Adopting an upper limit on the magnetic field at 0:01 pc of B 0:1 G (Reynolds et al. 1996b) limits to values smaller than 1. For = 2 , this constrains the acceleration radius to be r acc 3 jet = 3, = 1, and 10 pc, or 000 :06. On the other hand, the radius of acceleration cannot lie inside the Schwarzschild radius of the central black hole, which is of order 10 4 pc for a 109 M black hole. The dependence of racc on , , and the core magnetic field is too strong to make any detailed predictions about where the acceleration actually has to occur. However, the racc –curve is rather flat throughout most of the possible range for , which suggests that the most plausible value for racc falls between 1 and 10 pc. This is intriguingly far away from the central engine. 99 102 injection radius racc [pc] 10 1 10-1 10-2 10-3 10-4 0.2 Limited by Schwarzschild radius 0.4 0.6 0.8 σ 1.0 1.2 Figure 3.12: The minimum acceleration radius racc , as a function of (B / r ) for jet = 3 and LOS = 25Æ in the case of B / % (solid line). The dashed line shows racc for the case of % / r 2 and the same values of jet and LOS . The hatched area indicates the limit set by 10 Schwarzschild radii for the 109 M central black hole. The dashed-dotted line shows the (arbitrary) injection radius r0 = 000 :5 or 80 pc. 3.5 Chapter Summary We used the example of the M87 jet to demonstrate how broad band observations can be used to improve estimates of the physical conditions inside AGN jets. We showed that equipartition is not necessarily a good assumption in these jets. We also showed that the detailed radio surface brightness distribution and the spatial variation in the optical spectral index can both be explained by the same process: adiabatic compression of the jet plasma in relatively weak shocks. Fermi acceleration is not necessary (though not excluded) to explain the lack of cooling observed in the jet if we allow the jet to be moderately relativistic and the magnetic field to be below equipartition by a factor of a few. The external pressure required to confine the jet turns out to be comparable to what is inferred from X-ray measurements of the cluster environment. Chapter 4 Evolutionary Signatures of Radio Galaxies The previous chapter demonstrated how, given a few simple assumptions, we can measure the field strength in the resolved portion of a radio jet. There is a second crucial parameter we need to know in order to pin down the conditions within the jet: the jet power L. A relatively robust method is in place to estimate this quantity. Once again, though, this method relies on estimate of the magnetic field with the usual assumption of equipartition, and it is not clear how reliable it really is. In this chapter, we will propose a different method to complement measurements based solely on the total radio power in the lobes. Another motivation for the work in this chapter is that the evolution of radio galaxies has not yet been fully understood. Since radio galaxies pump large amounts of energy into the surrounding medium, we need to understand how the cluster properties change with time if they host a radio galaxy. This is important for cosmological arguments based on cluster masses through X-ray measurement and on the SZ-effect, but it is also crucial for our understanding of AGNs, since they must constantly be fed by the ambient material, and any disturbance of that medium will ultimately lead to a change in that feeding behavior. In other words, AGNs could be subject to strong feedback. The method discussed below could also be used to search for very young radio galaxies that are heavily obscured at long wavelengths by free-free absorption and would thus be hard to find in radio surveys, through X-ray observations. In this chapter we will discuss the X-ray signatures of expanding powerful radio sources. The following work has been published in Heinz, Reynolds, and Begelman (1998). 101 4.1 The Expansion of a Radio Galaxy: Connection Between CSOs and FRIIs In recent years there has been some progress in understanding how various classes of powerful extragalactic radio sources can be described in the context of an evolutionary picture. Recent radio surveys have identified classes of powerful sources which are morphologically similar to FR II radio galaxies but appreciably smaller. Sources less than 500 pc in extent have been termed Compact Symmetric Objects (CSOs; Wilkinson, Polatidis, Readhead, Xu, and Pearson 1994), whereas those in the size range 0.5–15 kpc are often referred to as Medium Symmetric Objects (MSOs; Fanti, Fanti, Dallacasa, Schlizzi, Spencer, and Stanghellini 1995). These classes of small sources, which form approximately one quarter of current flux–limited radio surveys, are thought to correspond to the early stages of full-sized FR-II radio galaxies (Begelman 1996; Readhead, Taylor, and Pearson 1996). Given this age template, we can attempt to build a self-consistent model of radio galaxy evolution. Central to our understanding of these sources is the following theoretical picture (first proposed by Scheuer 1974). Relativistic plasma flows from the central AGN in the form of collimated jets, passes through terminal shocks corresponding to the radio hot-spots, and inflates a ‘cocoon’ which envelops the whole source. This cocoon becomes highly overpressured with respect to the surrounding interstellar/intracluster medium and, hence, drives a strong shock into this material. The swept-up material forms a dense shell separated from the cocoon by a contact discontinuity (see, e.g., Begelman and Cioffi 1989). In the late stages of evolution, the expansion of the cocoon/shell becomes subsonic and the cocoon disrupts and mixes with the ambient medium. A cartoon of the general morphology of an intact source is shown in Fig.1.4. Although low-frequency radio observations do reveal well-defined synchrotron emitting cocoons (e.g., Cygnus-A; Carilli, Perley, and Harris 1994), there is relatively little direct observational evidence for the shocked shell. In principle, there are at least two methods of detecting the shell. Firstly, one can search for the optical line emission that is excited near the shock front (see, e.g., BB for an explanation of the H line emission in M87). Such line emission 102 is very sensitive to unknown parameters such as the fraction of cold material in the surrounding ISM/ICM and the ionization state of that material. Secondly, one can search for the X-ray emission from the shocked ISM/ICM and the associated cavity in the ambient material: Since the diffuse X-ray emission in clusters comes from the hot IGM, and since the cocoon material is dominated by relativistic plasma, which does not emit any significant amount of X-rays, the displacement of IGM by cocoon material will necessarily lead to a depression in X-ray flux. Cavities in the ICM have been observed in Cygnus A (Carilli et al. 1994), Hydra A (McNamara et al. 2000), Abell 4059 (for which we have been granted observing time on Chandra), and Perseus A (Böhringer et al. 1993). We argue below that at least in the case of Perseus A not only the cavity but also the shocked shell can be seen. Once we have confirmed that our model is a valid (be it crude) description of radio galaxy morphology and evolution, we can then apply this it to existing X-ray data and make predictions for future observations, specifically with Chandra. 4.2 Description of the Model 4.2.1 The Dynamical Model We first outline the basic assumptions used in our model to find a simple, robust descrip- tion of the early stages of radio galaxy evolution into a surrounding hot medium. Our model is based on the analysis by Reynolds and Begelman (1997). Following this work, we make several simplifying assumptions: (1) Spherical symmetry. For the purpose of this chapter it is sufficient to neglect the prolate structure observed in most radio sources, since more detailed hydrodynamics would be required in order to determine the shape of the cocoon beyond a self–similar form (see, e.g., Clarke, Harris, and Carilli 1997). The level of detail required in such simulations and the amount of computing power necessary to explore parameter space in the desired manner would defeat the scope of this chapter. The observed elongations are 103 moderate (axial ratios of order 3 in FR II sources, see Carilli et al. 1994). The dependence of our results on the source radius is relatively weak, which makes us confident that the application of our model to non-spherical sources will introduce minor errors only.1 (2) Purely relativistic gas inside the cocoon (i.e., the adiabatic index in the cocoon is c 4 ) and non-relativistic gas in the swept up shell ( s 3 = = 5 3 ). The latter assumption is valid in all but the early stages of the most luminous sources, in which the electrons become relativistic. (3) Uniform pressure. We take the pressure in cocoon and shell to be uniform and equal. This is a reasonable approximation in the context of the previous assumption, as the p sound speed inside the cocoon (c= 3) will be significantly higher than the expansion velocity of the shell. The radio hot spots will be overpressured, but we will neglect this complication in the following. (4) A King-model X–ray atmosphere provided by either the host galaxy or the cluster in which the AGN is embedded. The density profile thus behaves as: " r 2 (r) = 0 1 + rc # 3 2 ; (4.1) where 0 is the central density and rc is the core radius. can take any positive value; however, for the interface between cocoon and shell to be stable against Rayleigh– Taylor instability we need to assume < 2 (see below). 3 is observationally deter- mined by the ratio of the velocity dispersion of the cluster galaxies to the temperature of the cluster gas. (5) Non-radiative shocks. We neglect energy loss due to radiative losses in the equations below. This is justified as long as the cooling time is long compared to the source 1 A self-similar, non-spherical model has been advocated recently by Kaiser and Alexander (1999), however, the model is not self-consistent in that it assumes uniform interior pressure yet non-spherical expansion. 104 lifetime, a condition satisfied in the parameter range we consider. The system is well defined by energy conservation within the cocoon and the shell: c 1 Vc p_ + c V_c p = L(t) 1 (4.2) and s 1 4 Vs p_ + s V_s p = rs2 (rs )r_s 3 ; 1 2 (4.3) and the ram pressure condition at the shock: pc;s (t) = (rs )r_s 2 : (4.4) Here, Vs and Vc are the shell and cocoon volumes, respectively, rs is the shock radius, and pc;s = p(t) is the (uniform) interior pressure, which is a function of time. L(t) is the kinetic luminosity of the jets feeding the cocoon. A dot indicates a time derivative, i.e., p_ = dp=dt. Equation (4.4) holds only in the case of supersonic expansion, a condition well satisfied in the early evolutionary stages of our models but which is violated as sources pass a characteristic size. Once a source has decelerated below the ambient sound speed (typically of the order of csound < 1000 km sec 1 ) the evolution will resemble an expansion wave rather than a shock wave. The shell will thin out and eventually blend into the ambient medium; the cocoon– shell interface will become unstable and collapse on timescales of order the free fall time. The kinetic luminosity L(t) in equation (4.2) can in general be time dependent to allow for the intermittency suggested by Reynolds and Begelman (1997, see x4.5.1.1). For now, we will take it to be constant. In a sense, this can be interpreted as a time averaged luminosity LhL(t)i. To explore parameter space we have integrated equations (4.1) to (4.4) numerically over a time span of 108 years, assuming an initially small source. Our models were calculated over a grid of input parameters L and rc . We used the following parameter values: Luminosities ranging from of L = 1046 ergs sec L = 1042 to 1052 ergs sec 1 . We use a fiducial value 1 throughout the chapter except where indicated. Note that 105 luminosities in excess of L 1048 ergs sec 1 can be considered unphysical, since they correspond to Eddington luminosities for black hole masses > 1010 M . However, as L=0 is relevant to the dynamics, so we chose to hold 0 fixed and explore a wide range of L. Unphysically high values of L will be shown below, only the combination can be interpreted as relevant to sources in low density environments. Core radii in the range of 50 pc rc 500 kpc, with a fiducial value of 500 pc, typical of elliptical galaxies. We set 1 throughout the rest of the chapter, corresponding to 2 /r 1:5 for r rc . We fixed the central density to be 0 For power-law density distributions = 1:7 10 /r 25 g cm 3 or n e;0 = 0:1 cm 3. and constant, non–zero kinetic luminosity, a self-similar solution to the equations is possible. This solution is a good indicator of how the more general solution scales with the input quantities L, 0 , and rc . A necessary condition for a self-similar solution is that the cocoon radius rc be a fixed fraction of the shell radius, i.e., rc rs . Under these assumptions, equations (4.2) to (4.4) yield 1 9s 2 + 1 3 = 18s 2 8 rs (t) = r0 t 5 t0 3 (4.5) ; (4.6) where r0 is the shell radius at time t0 , which is defined by !1 0 r0 5 3 t0 = C1 L (4.7) with C1 " 363 (5 )3 (c 1) 3c 4+ 3 # 31 (4.8) It follows from equation (4.4) and the assumed pressure equilibrium between cocoon and shell that the shell temperature (assuming an ideal, non–relativistic gas) is proportional to the 106 square of the expansion velocity, r_s 2 . Thus, for a given r the temperature in the self-similar solution goes as T / r_s2 / 1=t0 2 / (L=0 )2=3 : Equation (4.6) reveals that solutions for (4.9) 2 (i.e., 2 in the limit 3 r rc ) are Rayleigh–Taylor unstable, since for those values the cocoon–shell interface is always accelerated and the shell is very dense compared to the cocoon gas. We can see from the basic set of equations that the only two parameters entering the solution are a radial scale factor (rc in the King-profile case, r0 in the self-similar case) and L=0 — this statement holds even for arbitrary density profiles. While rc and 0 can in principle be determined by direct observation, L can only be inferred theoretically from observed radio brightnesses. However, this conversion is not trivial and it would be very useful to constrain the kinetic luminosity directly. 4.2.2 Calculation of the X–Ray Brightness Because equations (4.1) to (4.4) do not specify the density and temperature structure inside the shell itself, we have to make additional assumptions about the radial dependences of and T . In this chapter we take both variables to be uniform within the shell and use the ideal gas law and mass conservation of the swept up material to convert from the pressure given by equation (4.4) to the temperature Tshell . The shock jump conditions dictate the values of shock and Tshock immediately behind the shock. In the case of a strong shock, the density jumps to shock 4preshock , and the temperature jumps to kTshock 2 (ss+1)1 2 r_s2 where is the molecular weight. Comparing shock and Tshock to the average shell values reveals that the shell is overdense in most cases, i.e., on average the shell is colder than the most recently shocked material, as is expected due to adiabatic expansion. The density ratio is 6 over most of the parameter range, close enough to the strong shock jump value of 4 to assume near uniformity of within the shell. 107 We calculate the specific X–ray emissivity due to thermal bremsstrahlung, taking the material to be composed of fully ionized hydrogen only (Rybicki and Lightman 1979): 25 e6 2 1=2 dW = T dV dt d 3mc3 3km 1=2 n2 e h=kT g : e (4.10) Since we are only interested in supersonic cases, we will have to discard parameter values for which the temperature drops below the ambient temperature Tambient 1 10 keV at a given radius. Because all high resolution imaging X-ray facilities available in the near future have bandwidths not far above this range, we can assume kT > h 13:6 eV, thus the Gaunt factor is given by the small angle uncertainty principle approximation: p 3 4 kT g = ln ; h where (4.11) = 1:78 is Gauss’s number. We also use equations (4.10) and (4.11) to compute the thermal bremsstrahlung emission from the hot galaxy/cluster gas, which we assume to be isothermal throughout the rest of this chapter. Clearly, the existence of a massive cold component to the ISM/ICM (as expected if a cooling flow operates) will alter the properties of the solution, in particular the emissivities, as relatively cold, dense material will radiate more efficiently. This aspect will be commented on in x4.5.1.2. 4.2.3 Observational Diagnostics Figure 4.1 shows the surface brightness results (i.e., the emissivity integrated along the line of sight) of integrating the model with our fiducial parameters. Shown are radial profiles at different times as indicated in the figure. Three basic features are identifiable from the figure, indicated by shadowed regions on the bottom of the plot: a) The flat part inside the shell, steepening into the bright shell. This component includes all lines of sight penetrating the cocoon, i.e., r < rc . b) The shell. We define this part as all lines of sight outside the cocoon but still penetrating the outer shell, i.e., rc < r < rs . 108 c) The undisturbed cluster emission, i.e., r > rs . This part simply tracks the King-profile atmosphere. In our case, since we used an index of = 1 , the surface brightness in 2 the power law part goes as r 2 and flattens into the core. We identify the following readily–measurable diagnostics which will be used in the rest of this chapter to investigate source parameters: i) shell-cluster ratio: the ratio of the surface brightness at the line of sight tangential to the cocoon (at rc ) to the surface brightness at the line of sight tangential to the shell (at rs ). The emission from the shell (without any contribution from the X–ray atmosphere) is brightest along the former line of sight. The latter is the brightest line of sight outside the region of shell emission. A high contrast is important for the detectability of the L=0 , we can see that brightness ratios are also going to depend on L and 0 only in the combination L=0 , since source. Since the dynamical solution depends only on the density normalization 0 cancels from equation (4.10). For a purely self-similar solution, we can thus expect this ratio to be proportional to T 1=2 / (L=0 ) 1=3 [see equation (4.9)]. ii) center-cluster ratio: the ratio of the surface brightness at the central line of sight to the surface brightness at the line of sight tangential to the shell. This ratio indicates if the central lines of sight are brightness enhanced or depressed compared to the cluster emission, i.e., if there is an ‘X–ray hole’. Again, since it is a brightness ratio, the center-cluster ratio should depend only on it should go as T 1=2 / (L=0 ) L=0 and rc, and for the self-similar case 1=3 . The presence of a strong point-like AGN X-ray component will swamp the cluster emission at the very center. Because the brightness profile is very flat at central lines of sight (as can be seen from Fig. 4.1), we can avoid the contamination by taking an off-center value for the central surface brightness and will only make a small error. 109 0.15 0.61 2.33 8.76 nomenclature brightness [arbitrary units] 0.03 rc rs a 0.1 b 1.0 c 10.0 r [kpc] Figure 4.1: Source evolution, seen through a flat 1 5 keV bandpass for our fiducial parameters (see x4.2). The x-axis is in units of kpc, the y-axis in arbitrary flux units. The different curves correspond to radial profiles at different times as labeled in the figure (in units of 106 years). The thick grey curve corresponds to t = 0, i.e., the undisturbed cluster profile. iii) shell count rate : the integrated count rate from all lines of sight penetrating the shell (in other words: all of areas a and b in Fig. 4.1), including back– and foreground emission from the X–ray atmosphere. This quantity is easier to determine than the background subtracted emission from just the shell. Notice, however, that since it depends on absolute normalization, both the distance to the object d and the density normal- ization 0 factor into the shell count rate , thus we cannot express it as a function of L=0 and rc only, rather, a factor of (0 =d)2 remains. The particular values of these diagnostics for a given source will depend on the assumed instrumental response, as the cluster and shell have different temperatures and thus different 110 spectra. In the following we will use both the ROSAT HRI band and the Chandra ACIS-S band as indicated. 4.3 Applications to Existing Data 4.3.1 Perseus A Figure 4.2 shows a 50 ksec ROSAT HRI exposure of Perseus A2 . Per A is a radio galaxy with an estimated kinetic power of > 1043 ergs sec 1 (Pedlar et al. 1990), at a redshift of 0:02 or 80 Mpc h75 1. It is located in a dense cluster environment with core densities of n0 0:02 0:1 cm 3 , a core radius of rc > 50 kpc, and a temperature of 7 keV (see z White and Sarazin 1988). The elliptical shell structure is readily visible from the plot and has been the subject of a paper by Böhringer, Voges, Fabian, Edge, and Neumann (1993). The shell semi–minor and semi–major axes are approximately to 12 and 17 kpc for a Hubble constant of 3000 and 4500 , respectively, corresponding H = 75 km sec 1 Mpc 1 . Because the shell is so well–defined over a significant angle, we are confident that the source is still in supersonic expansion or has only recently crossed the sound barrier. It is also obvious from the image that our assumption of a spherically symmetric, stationary cluster medium is idealized — the bright feature to the east indicates that “cluster weather” has probably had a significant impact on the appearance of the structures. However, the brightness changes are moderate and, keeping in mind those caveats, we feel justified in applying our model to this source with some caution. We have computed our model for a grid of various rc and L. The cluster gas was assumed to have a temperature of kT 7 keV and a central density of n0 = 0:1 cm 3 . The integration was stopped at a size of 16 kpc, the approximate size of the source. We computed the three diagnostics described in x4.2.3 assuming the ROSAT passband. We also calculated the region in rc –L space for which the source is still supersonic. L=n0 must exceed 5 1046 ergs cm3 sec 2 We find that for a core radius rc 1 , and for a density of n 0 0:02 cm These data were obtained from the LEGACY public archive situated at GSFC (NASA). > 50 kpc, 3 , the mean 111 Declination (2000) ile 3 e2 of pr of il pr 30″ profile 4 32′ 00″ 31′ 00″ 30″ 30′ 00″ e5 il of pr profile 1 41° 29′ 30″ 55s 50s 03h 19m 45s Right Ascension (2000) Figure 4.2: A 50 ksec ROSAT HRI exposure of Per A, smoothed with a 2 arcsec Gaussian beam. We have chosen the contrast to emphasize the shell structure. These data were downloaded from the LEGACY public archive at GSFC (NASA). The black lines show the paths along which we chose to take brightness profiles for our diagnostics. kinetic luminosity must be L > 1045 ergs sec 1 to satisfy the supersonic condition. The shaded region in Fig. 4.4 shows the region in parameter space which is forbidden if we insist that the source be supersonic. To compare these models to the data for Perseus A, we took radial brightness profiles at several selected locations (shown in Fig. 4.2 and Fig. 4.3). We decided to hand-pick these 112 profile 1 2.00 1.35 1.00 profile 2 1.6 count rate [arbitrary units] 1.1 1.0 profile 3 1.30 1.12 1.00 profile 4 1.35 1.00 profile 5 1.9 1.4 1.0 Figure 4.3: Brightness profiles 1 through 5 according to Fig. 4.2 in arbitrary units. locations rather than assign them randomly due to the complications caused by the “cluster weather” we pointed out earlier. The enhancement at the shell compared to the brightness just outside (i.e., the shell-cluster ratio) is roughly3 a factor of 1:3 2. The region correspond- ing to these values in parameter space is shown in Fig. 4.4 as a vertically hatched area with a dashed border. Approximating the core–subtracted central surface brightness by the brightness 3 The HRI resolution is of order 4 arcsec, which is roughly the expected width of the shell at a radius of 40 arcsec (see equation 4.5), thus we expect the shell to be just marginally resolved. The brightness ratios we extract from the image will thus be lower limits. The core is the dominant feature and will have to be removed. 113 minimum between core and shell, we find a brightness ratio of the interior against the cluster immediately outside the shell (i.e., the center-cluster ratio) of 1 1:3. The region in rc – L0 space compatible with this condition is also shown as a hatched area (horizontal lines) with a dotted border in Fig. 4.4. We also estimated the total count rate for the shell area (i.e., the shell count rate from x4.2.3) to be 0:64 s 1 from taking an elliptical ring aperture. To display the predicted total count rate in the same plot we will have to remove a factor of (0 =d)2 from this value (see section 4.2.3). Using the assumed density from White and Sarazin (1988) of 0 0:02 0:1 cm 3 and d = 80 Mpc, we can calculate the corresponding diagonally hatched area in Fig. 4.4. White and Sarazin (1988) provide an estimate for the core radius of rc 10 kpc, whereas White, Jones, and Forman (1997) chose a core radius of 150 kpc. These values for rc are shown as two thick, dash–dotted lines in Fig. 4.4.4 Together with the other constraints in Fig. 4.4, these estimates allow solutions in a range of L46 =n0:1 from 5 10 1 to 5 102 . The lower end of this range can be ruled out by the requirement of supersonic expansion. Keeping in mind the rather large uncertainty introduced by our measurements and in the input parameters we used we find that the different areas in Fig. 4.4 match up in a self–consistent fashion. The fact that the average kinetic luminosity is L > few 1045 ergs sec 1 is in itself a very interesting result, as it suggests that the total power output of Per A is significantly higher than the simple estimates based on the equipartition energy content of the cocoons (Pedlar et al. 1990). A possible conclusion might be that equipartition is not a good approximation in this case (the particle pressure will most likely exceed the magnetic pressure). It is interesting to note that a kinetic power estimate based on the conversion factors by Bicknell, Dopita, and O’Dea (1997) suggests that the instantaneous kinetic luminosity is L< 1044 ergs sec 1 . Hence this may be evidence that Perseus A is in a relatively quiescent state (maybe corresponding to the “off” state of Reynolds and Begelman 1997). 4 Note that, even though there is more than an order of magnitude discrepancy between those values, the models constraints are virtually the same for both values. Formally, the larger value provides a better fit. 114 rc[kpc] 100.0 c) 10.0 1.0 b) a) 0.1 10-4 10-2 100 102 L46/n0.1 104 106 Figure 4.4: Model contours in parameter space for Perseus A, assuming isothermal cluster gas at 7 keV and a shell size of 16 kpc, seen through the ROSAT HRI response. The three hatched regions correspond to the observational diagnostics described in x4.2.3: a) the observed shellcluster ratio of 2 (hatched vertically), b) the observed center-cluster ratio of 1:1 (hatched horizontally), and c) the limits set by the observed shell count rate of > 0:64 counts sec 1 and 3 the estimated central density of n0 < 0:1 cm (White and Sarazin 1988, , hatched diagonally). Keep in mind that the predicted count rates for a given L=0 and rc still scale with an additional n0 2 , thus the count rate only allows us to set limits in this plot. The grey area shows the subsonic region in parameter space. The two thick dash–dotted lines correspond to the estimated core radius of Per A (White et al. 1997; White and Sarazin 1988). It should be noted here that an as of this date unpublished Chandra observation of Perseus A exists (Fabian, private communication), that seems to indicate that the shocked shell temperature is in fact below the ambient temperature. This result, if it holds up under scrutiny, is clearly inconsistent with our model, as the shocked shell must always be hotter than the un-shocked environment. An obvious explanation for this discrepancy would be that the external medium is in 115 fact non-homogeneous, containing clouds of cold material, which, upon being shocked, would radiate very efficiently, thus lowering the shock temperature. Efforts are underway to investigate the effects of a two-phase IGM on the observational effects discussed in this chapter. 4.3.2 Other Examples Another well known source which exhibits an X–ray structure similar to the one we pro- pose here is Cygnus A. This source has been object of an extensive study by Clarke et al. (1997), who ran a 3–dimensional simulation of a jet advancing into a surrounding cluster medium. Even though there are cavities and brightness excesses visible at the center and the rim of the cocoon, respectively, the structure is not nearly as reminiscent of a shocked shell as the one in Per A. It is more than twice as distant as Perseus A and also exhibits a much stronger cooling flow, both of which will tend to make the analysis we suggest harder. We therefore decided not to apply our method to this source, although this would be an excellent target for application of our model once future high resolution data are available. There are a number of other sources for which suspicious holes in the X–ray morphology have been detected, for example in Abell 4059 and Hydra A (McNamara et al. 2000). Hydra A is intrinsically less powerful and spherical symmetry is clearly broken in this object, possibly due to the source being subsonic. More detailed modelling of such sources, with the help of numerical simulations, is necessary to understand this source. We have been granted Chandra time to observe Abell 4059 scheduled for late 2000. 4.4 4.4.1 Predictions for (Chandra) Observations Detectability of Young Sources Young sources are generally hard to detect in all wavelength bands, because they are small and evolve quickly, so we expect the local density of young sources to be very small, whereas distant sources will be faint and unresolved. They will be particularly hard to detect if 116 they are in an “off-state” (in the sense of Reynolds and Begelman 1997), in which case radio surveys will most likely select against them, since the radio hot spots fade away quickly and the spectrum becomes very steep. In such cases, optical observations of shock-excited H emission, and the X–ray emission that we are investigating here could provide ways of finding such candidates. The main issue with these sources is detectability. The best spatial resolution available in X–ray imagers today is 0.5 arcsec (Chandra HRC) to 1 arcsec (Chandra ACIS, taking account of proper oversampling). Thus, in order to resolve a source, it has to subtend more than 2 arcsec on the sky (this assumes that the core, which is by far the dominant feature, will not contaminate more than the central resolution element). But even if a source can be resolved, we shall show that extremely long observing times will be necessary to achieve significant signal–to–noise: even though the surface brightness is higher for small sources, the cluster brightness also rises toward the center. We have calculated the three observational diagnostics from x4.2.3 for a source of size 500 pc over a grid of 2100 parameter combinations of rc between 50 pc and 500 kpc and L between 1042 to 1052 ergs sec 1 , assuming the Chandra ACIS-S passband. The result is shown in Fig. 4.5. The shell temperature is generally higher for small sources. Fig. 4.5a shows the temperature as a function of L=0 and rc for a shell radius of 500 pc. The hatched region shows the parameter values for which a source of this size at the fiducial cluster temperature of 4 keV has become subsonic. Even at such a young age, we see that low power sources or sources in a very dense environment have already stalled. For higher luminosities the solution is well behaved and basically follows the scaling relations (4.6) - (4.8). For very high luminosities/low densities the temperature formally reaches values in excess of 100 keV, beyond which our model is certainly not valid, as we assumed the shell gas to be strictly non–relativistic. Figure 4.5b shows the calculated shell count rate for a source at a distance of 100 Mpc, 3 2 . Since normalized to a central density of n0 = 0:1 cm 3 , so what is plotted is 0:1 ncm 0 increases with n20 , sources in dense cluster environments will be much easier to detect. The 117 figure shows that for big and dense clusters we might hope to detect a sufficient number of the photons from the shell. In addition to a high count rate a second issue for detectability is the contrast of the shell structure (i.e., the shell-cluster ratio). Fig. 4.5c shows that the shell-cluster ratio is significant over a large range of luminosities and core radii. However, for sources still within the core of the cluster profile the ratio drops and approaches one (i.e. undetectability), since in such cases the line of sight passes through a deep fore- and background screen of cluster gas, which tends to swamp out the shell emission. Thus we have a detection dilemma: For sources with large core radii, the count rates are high but the contrast is small. For sources which have broken out of the flat part of the cluster gas, the contrast is high, but the count rates drop. There is an optimal range in core radius and luminosity, which is the larger, the higher the density of the host environment is. Figure 4.5d shows the center-cluster ratio to indicate whether we see the cocoon as an X–ray hole or whether it shows a brightness enhancement relative to the cluster gas. In the presence of a bright core, it will presumably be easier to detect a source which shows a central brightness depression against the cluster, since in such a case we will see a dark ring between core and cluster. We conclude that the redshift constraints and the fact that bright cores will tend to render the shells of barely resolved sources invisible (i.e., the core will swamp out the shell) poses a serious problem for the detectability of young sources. Generally, though, it should be possible to detect close sources in sufficiently dense environments. The detectability constraints have been compiled in Fig. 4.6. This figure has been constructed as follows. For a given set of source parameters and distance, we calculate the count rate in the ‘observed’ shell (i.e. the annulus between rc and rs ), Cshell . We also compute the count rate in an annulus of the same area lying just outside the observed shell, Ccluster . The shell is deemed to have been detected if the brightness profile is seen to possess a jump at rs . Thus, we calculate the exposure time needed to measure Æ = Cshell Ccluster to within 30 per cent (i.e. the exposure time required 118 to demonstrate the non-zero value of delta to 3 sigma confidence). We have used L46 =n0:1 and rc = 500 pc and rc = 5 kpc. =1 In terms of detectability this is a more meaningful quantity than the actual brightness ratio of the two rings, since a source is only detectable if there is a visible jump in brightness across the shell. 4.4.2 Extended Sources As was explicitly shown in x4.3.1 for Perseus A, application of our observational diag- nostics to a well resolved source can place constraints on the source parameters, especially if the core radius of the cluster is known. We have computed our three observational diagnostics from x4.2.3 for a much more extended source of size 16 kpc, as shown in Fig. 4.7. At this size, only powerful sources will have maintained a supersonic coasting speed, and we can expect the transition between super– and subsonic sources to be a strong indicator of the overall source power, since the break in the data happens at a well defined value of Tcluster . L=0 for given core radius rc and cluster temperature The temperature shows the dependence on core radius and power we expect from the scaling relations in equations (4.6)-(4.8). Because large sources (by definition) subtend a larger solid angle, their count rates can be much higher than those for small sources, even though the peak shell surface brightness decreases. Since we include the fore– and background cluster emission in the shell count rate (shown in Fig. 4.7b), this effect becomes even more pronounced. Also, since the shell will likely be resolved and separated from the core, the recognition of the structure itself and the reduction of shell parameters will be simpler than for small sources. The strong dependence of the shell count rate on the core radius for rc < 16 kpc is introduced because we fixed the central density, thus the mass enclosed in a sphere radius rs (i.e., the swept up mass) increases with the core radius, and so does the shell density. For rc > 16 kpc the dependence is not as strong. In this case, it is produced by the fact that we integrate over a longer line of sight of undisturbed cluster gas within the core for larger rc . As in the case of Perseus A, we can see that the total count 119 rates are in a comfortable regime to achieve good statistics over a wide parameter range for a cluster with our fiducial density. If the core radius can be measured by other means (e.g., from optical or X-ray data) and if the redshift of the source is known, the brightness ratios in Fig. 4.7c and 4.7d can be used to constrain L=0 to no more than two possible values in the L=0 –rc –plane, independently from the total count rate (if the supersonic condition is applicable we can fully constrain this parameter in many cases). In this case, the total count rate can be used to determine 0 and L separately, and thus measure the age of the source. Density, age, and in particular the kinetic luminosity will be useful input into jet models. With Chandra ACIS-S it is feasible to obtain imaging spectra from resolved sources. In the case of ACIS with a spatial resolution of about 1 arcsec, the source has to be larger than 2 arcsec in radius, thus the redshift restriction will be z < h75 =8. interested in the bremsstrahlung emissivity goes as T 1=2 e h=kT shell temperature is mainly dependent on In the regime we are ln [kT=(h )], and since the L=0 , spectra are very useful to separate out this parameter. A color–color–image would emphasize regions of different temperature (i.e., the shell versus the undisturbed X-ray atmosphere). For high enough count rates it will even be possible to obtain information about the foreground absorption. Spectra can also give a handle on the composition of the cluster gas from spectral line analysis. 4.5 4.5.1 Discussion Complications The model we have discussed in the previous sections offers a simple way of probing the radio source structure and determining important parameters. However, since it is a gross oversimplification of reality, we have to discuss several complications. 120 4.5.1.1 Intermittency As recently proposed by Reynolds and Begelman (1997), a large population of sources might be intermittent (i.e., strongly time variable in their kinetic energy output), thereby explaining the observed size distribution of CSOs and MSOs, which shows a previously not understood flattening at small sizes. This could be due to the fact that sources spend a significant fraction of their lifetime in a quiescent state, in which the jets are turned “off”. In such a case, the shell and the cocoon are still expanding, but they will slow down and the shell will thicken. Since a large part of the radio luminosity comes from the radio hot spots, which fade away rapidly, the radio luminosity also decreases. Whereas for large sources the cocoons filled with relativistic plasma provide enough emission to be detected in the radio, young dormant sources will be very hard to detect with radio observations. Thus we might hope to detect the X–ray signatures of such sources. The major difference that has to be incorporated into our analysis is a time variable L(t) instead of L in equation (4.2). Since we integrated the equations numerically, this change presents no difficulty. For simplicity we followed Reynolds and Begelman (1997) in using a “picket-fence function” for L. We chose a duty cycle of 10%, i.e., the source is “on” for 10,000 years and “off” for 90,000 years. Depending on the average source power, this happens at different evolutionary stages of the source, thus we should expect to see changes from the previous figures. However, as the source grows, the influence of the intermittency becomes smaller and the behavior approaches the solution for constant luminosity, corresponding to an average power of L = hL(t)i. essentially unaltered. For large sources, the results we presented above are therefore 121 4.5.1.2 Cold Material and Mixing An important unknown we have neglected to include in our treatment is the possible multi–phase nature of the host ISM/ICM. A cold or warm phase5 would be hard to detect in an X–ray observation, although it can sometimes be seen via X-ray absorption (Allen et al. 1995; Fabian 1994). Spectra could help in finding multiple temperature components in the continuum emission and abundances of low ionization states from spectral lines and edges. The presence of a cold component could severely alter the dynamics of our expanding shell if both filling factor and mass residing in the cold phase were high enough. The general picture is that, as the shell reaches the cold blobs of material, a shock is driven into the cold matter with the same strength (i.e., same Mach number) as the shock into the ISM/ICM, since the cold and hot phases are assumed to be in pressure equilibrium. The cold material will therefore be heated and radiate either in the X–ray regime (if it is hot enough) or in the UV/optical. Depending on their sizes, the blobs could either be completely evaporated or their remnants might remain inside the cocoon. It might get shredded by hydrodynamical instabilities, in which case it would mix with the shocked gas and the cocoon plasma. The cold material could cool very efficiently and might radiate away a lot of the shell energy. Since recent Chandra observations of Perseus A seem to indicate the presence of cold material inside the shocked shell, it is of key importance to include these effects in future applications of this model. Future work will also concentrate on the optical line emission we would expect to see from such filaments (see, e.g., BB). A related question is the possibility that dynamical instabilities (e.g., Rayleigh-Taylor, Kelvin-Helmholtz) could mix material from the shell and the cocoon, producing pockets of non–relativistic material in the relativistic cocoon. If mixing is strong, a curtain of intermediate temperature material could form and absorb radio emission from the cocoon, thus producing the characteristic spectral shape of Gigahertz Peaked Sources (GPS), as described by Bicknell, 5 There is now mounting evidence for the existence of large amounts of warm, T 105 K gas in clusters, Buote 2000 122 Dopita, and O’Dea (1997). We are currently investigating this effect with the help of numerical simulations, guided by the dispersion relation of relativistic, cylindrical Kelvin-Helmholtz instabilities. Foreground absorption might also affect our observational diagnostics. Even though the column density of Galactic material is well known in most directions, the presence of a cold component in the host cluster could have a significant effect on the detected signal. As long as the covering factor and the filling factor of the cold component are small, this effect should be negligible. If, however, the cold matter covers a large cross section of the source with sufficient column density, absorption can change the spectral shape and therefore alter not only the total expected count rates but also the brightness ratios, as they depend on the temperature difference between the shell and the cluster. Current data suggest that typical values for the column density of NH of cold material intrinsic to such sources are of the order NH 1021 cm 2 , too low to affect the Chandra band significantly. 4.5.1.3 Density Profile Clearly, an isothermal King profile is a gross oversimplification of reality, but it should at least provide us with a first order approximation. Introducing two separate King profiles (one for the cluster, one for the Galaxy itself) might provide a better description of reality, but it would also increase the number of free parameters by three (rc ; 0 , and ), all of which would have to be determined by other means to improve this analysis. We decided that the increase in realism would not justify the necessary computing time and the uncertainty as to which values we should chose for the new parameters. 4.5.2 Chapter Summary We presented a model for radio galaxy evolution and the interaction of radio galaxies with their environment. This model can be used to calculate the observational signatures of this interaction, manifesting itself in the form of cavities blown into the ISM by the radio lobes and 123 in a strong shock surrounding these cavities. We showed how this model can be used to infer physically important parameters of the radio galaxy, such as the average total kinetic power. Our analysis of Perseus A demonstrates that the power in its jets might be much larger than that inferred from traditional estimates based on equipartition arguments. Furthermore, our model suggests how Chandra observations can be used to detect very young radio galaxies which would be obscured at longer wavelengths. Our scheduled Chandra observations of the cluster Abell 4059 and its strong central radio galaxy will be analyzed on the basis of this model. Future research will concentrate on the effects of non-uniform external media, nonsphericity, and dynamical instabilities occurring at the cocoon-shock interface. 124 b) shell counts 100.0 10.0 10.0 rc [kpc] 100.0 10 0 rc [kpc] a) Temperature 0.1 10-4 -3 10 10-2 10 4 10 6 1.0 10 2 1.0 10-1 -5 10 0.1 100 102 L46/n0.1 104 106 10-4 c) shell-cluster ratio 10-4 0 4.0 . 8 00 10.0 1.0 0 2.0 4.0 16.0 10-2 106 1.00 rc [kpc] rc [kpc] 2.00 0.1 104 1.00 100.0 10.0 1.0 100 102 L46/n0.1 d) center-cluster ratio 1.00 100.0 10-2 0.1 100 102 L46/n0.1 104 106 10-4 10-2 100 102 L46/n0.1 104 106 Figure 4.5: Contour plots of the shell temperature and our three diagnostics (see x4.2.3) as functions of the source parameters rc and L=0 for a source with shell radius 500 pc at a distance of p 100 Mpc. The contour levels are separated by factors of 10 in plots a) and b) and by factors of 2 in plots c) and d). We assumed the Chandra ACIS-S response. The grey area on the left side of the plot indicates parameter values for which a source of this size has turned subsonic for a cluster temperature of 4 keV. The following quantities are shown: a) Temperature in keV, 2 b) shell count rate , normalized to n0 = 0:1 cm 3 , i.e., 0:1 cm 3 =n0 . At large core radii, cluster emission dominates, producing horizontal lines in the figure. c) shell-cluster ratio, d) center-cluster ratio. 125 1.000 rc=500 pc L=1046ergs sec-1 z 0.100 0.010 64 4k 0.001 101 1.000 pc kp c p 1k c 50 0p c 25 102 103 104 t [sec] 0p c 105 106 rc=5 kpc L=1046ergs sec-1 64 kp c z 0.100 4k pc 0.010 2k pc 1k pc 50 0.001 101 102 103 0p 104 t [sec] c 25 105 0p c 106 Figure 4.6: Detectability constraints. This figure shows the exposure times needed to measure Æ, the difference in the count rate from the annulus between rc and rs to the count rate from an annulus of equal area lying just outside rs , to within 30 per cent. This demonstrates the non-zero value of this difference to 3 sigma confidence. The lines correspond to different source sizes as indicated in the figure. They are terminated when the spatial resolution limit of Chandra ACISS is reached, i.e., when the source becomes smaller than 4 arcsec across. Since it is properly oversampled, the Chandra HRC has twice the resolution, but a lower effective area and no energy resolution. The symbols correspond to different sources we picked to demonstrate what can be achieved. Star: VII Zw485, square: Per A, diamond: 4C34.09, triangle: NGC1052. 126 b) shell counts 100.0 100.0 10.0 10.0 rc [kpc] -1 10 1.0 -3 10 10 4 10 2 10 0 1.0 1 10 0.1 -5 10 0.1 10-2 100 102 L46/n0.1 104 106 10-4 10.0 0 1.0 1.0 2.0 4.0 8.0 0 1.0 1.0 0 10.0 rc [kpc] 100.0 16. 104 106 d) center-cluster ratio 100.0 0.1 10-4 100 102 L46/n0.1 1.00 rc [kpc] c) shell-cluster ratio 10-2 2.0 10-4 4.0 rc [kpc] a) Temperature 0.1 10-2 100 102 L46/n0.1 104 106 10-4 10-2 100 102 L46/n0.1 Figure 4.7: Same as Fig. 4.5 for a source of 16 kpc radius. 104 106 Chapter 5 A Shotgun Model for Gamma-Ray Bursts 5.1 Introduction While it is not known if GRBs are in fact collimated outflows, they are certainly ultra- relativistic (even more so than AGN jets). Their interaction with the environment is well established and key to our understanding of GRBs, as afterglows have revolutionized the science of GRBs. In fact, it has yet to be proven that the GRB is not itself due to the interaction of a relativistic outflow with its environment. In this chapter we will argue that just such an interaction, in a configuration not previously considered, might be the key to solving the GRB puzzle. The main observational features of GRBs were introduced in x1.2, including the two main features for any GRB theory to explain: the enormous energies released in only a few tens of seconds, as well as GRB variability. As established in x1.2, GRBs are probably produced by shocks in a relativistic flow. This flow must be launched before it can shock. As in the case of AGNs, the most efficient energy production mechanism available is the release of gravitational potential energy of matter falling down the gravitational well of a compact object. The short timescales and the absence of nuclear activity in typical GRB host galaxies suggest that the central engine of GRBs is built around stellar mass black holes rather than massive ones. Typical GRB energies are comparable to the gravitational energy released by about a solar mass of material accreting onto a compact object, supporting the notion of stellar central engines. The two most popular mechanisms for rapid release of such large amounts of energy are mergers of compact objects, with at most one 128 of them being a black hole (otherwise the energy would be released exclusively in the form of gravitational energy) and extremely energetic supernovae, dubbed hypernovae. In the case of a merger of two non-singular objects (i.e., N.S. — N.S., N.S. — W.D., W.D. — W.D.), a black hole forms quickly, around which an accretion disk of residual material releases its energy over a viscous timescale, roughly comparable to the length of the observed burst. Similarly, in a hypernova, believed to occur in massive stars with M > 35M , the initial collapse produces a black hole of mass 10M , while the stellar mantle collapses to a thick accretion disk. While the exact mechanism of energy release and GRB formation is still unknown, the result of this energy release is, in most cases, rather similar: a large amount of radiation released in a small volume (comparable to the gravitational radius of the central object) will immediately reach a state of pair equilibrium, with very large opacities and any radiation present will be unable to escape. The specific internal energy of this material is large enough for it to be unbound and expand freely, essentially like a bomb. The internal energy in the plasma is dominated by relativistic forms of energy, shared by radiation, magnetic fields, and pairs, and the flow will accelerate to relativistic bulk speeds very quickly. Such a scenario is called a fireball, since the (extremely hot) gas will expand spherically in the absence of any external means of collimation. Acceleration will continue until the internal energy has been converted adiabatically into kinetic energy, with the terminal Lorentz factor approaching the ratio of the initial internal energy density to rest mass energy density in baryons (see also x2). Independently of GRBs, this scenario has been investigated by Blandford and McKee (1976). Once it has reached its terminal 1, the material will form a shell of thickness comparable to the size of the initial fireball at rest (as seen from an observer stationary in the frame of the central engine). This shell is the starting point for most GRB models. 5.1.1 External Shocks In the first serious GRB model (Rees and Meszaros 1992; Katz 1994b; Sari and Piran 1995), the coasting shell sweeps up ambient material in a double-shock structure. This shock 129 is the origin of the observed radiation, which is why this model has been called the ”external shock model”. The shell will have transferred most of its kinetic energy into internal energy of both the forward shock into the ISM and the reverse shock into the shell when it has swept up a fraction of 1= of its own mass. This is because the swept-up material is shocked, with post-shock particles reaching random Lorentz factors comparable to the shock Lorentz factor , boosting the inertia of the swept up material by a factor of order energies, 100, and an ambient density of n 1 cm . For typical GRB 3 , this occurs at a distance of order 1016 cm from the center, leading to an observed emission time scale of order 10 100 sec, comparable to the light crossing time of the shell itself (which is not compressed by relativistic effects). The energies and spectra from such a shock match the observations well, however, the model cannot reproduce the observed millisecond timescale variability, since the produced radiation is emitted in a single, broad spike of length . In order to explain the fast variability, it has been argued that the external medium might not be uniform (e.g., Shaviv and Dar 1995; Fenimore et al. 1996), thus leading to spikes in the emission whenever the shell encounters a cloud. There is ongoing discussion about the validity of this argument, due to what Sari and Piran (1997) call the angular spreading problem, illustrated in Fig. 5.1: the observer will only receive radiation originating from an area of the shell with viewing angles LOS < 1= with respect to the motion vector of that material due to relativistic beaming. A shocked cloud of radius r at a viewing angle 1= will have a projected depth of order Æ r= < R 2, where R is the radius of the shell. For typical ISM densities, these clouds must be so small in order to explain the short term variability that they can only cover a very small fraction of the shell surface, and the efficiency of the conversion of shell-kinetic energy into radiation must be correspondingly small (Sari and Piran 1997). Dermer and Mitman (1999) argue that clouds very close to the line of sight produce much shorter spikes while at the same time contributing a relatively large fraction of the flux. However, such a model implies a trend for spikes in the lightcurve to become broader at later times in the burst, which is not seen in the observational 130 r 1/Γ r r Γ Γ central engine clouds Figure 5.1: Illustration of the angular spreading problem in the dirty fireball model (Dermer and Mitman 1999), which employs clumpy external medium in the attempt to rescue the external shock model. data. Fenimore et al. (1996, 1999a, see also Woods and Loeb 1995) recently suggested that an external shock scenario could give rise to the observed variability if the spherical symmetry of the outflow were broken, still in the context of what Sari and Piran (1997) call a ‘Type I’ model, i.e., the burst duration is set by the slowing-down time of the ejecta. Once again, though, the observed temporal constancy of the pulse width in individual spikes of GRB990123 seems to rule out such a model (Fenimore et al. 1999b). 5.1.2 Internal Shocks The difficulties of the external shock model to explain the short term variability prompted Sari and Piran (1997) to postulate that the gamma ray emission must instead be produced by the internal shock scenario (Narayan et al. 1992; Rees and Meszaros 1994). The emission in this model is produced by internal dissipation of kinetic energy without the need for an external agent. While other means of dissipation are possible (e.g., inverse Compton scattering losses of turbulent field energy, as proposed by Thompson 1994), the most popular incarnation of the internal dissipation scenario simply involves shocks of ultra relativistic shells moving at different bulk Lorentz factors . Each time two shells collide, a spike of radiation is released. In this 131 picture, the duration of the burst T is set by the time scale over which the central engine operates, while the substructure in the bursts on time scales is produced by the inhomogeneities in the outflow. As in the external shock model, the signal received by the observer is spread out due to the curvature of the shock front. Assuming spherical shocks, this spread in time is of order Æ R=(c 2 ), where R is the radius of the shell, as evident from Fig. 5.1. For inter-shell distances corresponding to the observed spike distribution and for for the shocks to catch up with each other is of order > 100, the typical radius 1012 cm, and the angular spreading time is of order a few milliseconds, shorter than the observed burst substructure. Thus, unlike the external shock model, the internal shock model can explain the variability in GRBs. However, recent estimates of the energy conversion efficiency indicate that, at best, a few percent of the bulk kinetic energy carried by the outflow can be converted into gamma rays in internal shocks, which leads to uncomfortably high requirements on GRB energies (Panaitescu et al. 1999; Kumar 1999). Larger efficiencies can be achieved if very large dispersion in is assumed(Katz 1997). A non-spherical geometry can also reduce the required energy, however, a very small opening angle of the outflow implies a high rate of unobserved GRBs, which is hard to reconcile with the number of observed supernovae (which are believed to produce GRB precursors - either compact objects or hypernovae, as explained in x1.2). 5.2 The Shotgun Model In this chapter we propose a different way by which substructure in the outflow can produce a GRB, also via the interaction with the external medium, but in a ‘Type II’ scenario, i.e., the duration of the burst is set by the lifetime of the central engine (Heinz and Begelman 1999, see also Chiang and Dermer 1999; Blackman et al. 1996). In our model, the outflow itself is very clumpy, with most of the energy concentrated in small blobs, which are sprayed out with high over a small opening angle. These bullets then slam into the surrounding medium (not unlike a meteor shower or a shotgun blast), where they release their kinetic energy and produce gamma ray emission via external shocks. This scenario is illustrated in Fig. 5.2. 132 Γ 1/ θ LO S low erg Aft B GR g stin Coa n atio eler Acc Figure 5.2: Illustration of the shotgun model. In the context of our model, the spikes in BATSE lightcurves are produced by individual bullets of cold ejecta slamming into the surrounding medium. As we will show, a distribution of masses and/or Lorentz factors of these bullets can reproduce the observed signatures of GRBs reasonably well. In the following we assume that the central engine of the burst releases a number of bullets N 0 distributed over a fan of opening angle of 10Æ with Lorentz factor 1000 3 10 100 s. Each bullet is assumed to expand sideways with a velocity of v? = = 10 2 2 = 1= , measured in the observer’s frame ( is the sideways velocity in the comoving frame). The assumption that 1 implies that the internal and released over a time period of T expansion speed is very sub-relativistic. Since 1= , we only see a fraction of the total released energy, Eobs = 1047 133 E53 = 3 2 ergs (where E is the inferred isotropic energy in units of 1053 ergs) and an observed 53 number of bullets N 100 N100 = N 0 =(2 2). It is essential in our model that the covering fraction be less than unity (otherwise it would turn into an internal shock model), thus we require p < 1= N . A bullet of mass Mb = 5:5 10 3 13 E M =N 53 100 3 will have converted half of its kinetic energy into internal energy (which can subsequently be radiated away as gamma rays, see below) after it has swept up or ploughed through a column of interstellar gas of mass Ms 10 3 3 s, then the length over which the material is swept up must be of the order of R = 3 1013 3 3 2 cm. If the ambient density is namb 108 n8 cm 3 , the required Lorentz factor is Mb = . If the duration of the observed spike is s = 2300 E53 2 2 N100 1=8 3 3 n8 (5.1) This model fails for low ambient densities, as has already been discussed in the literature (e.g., Sari and Piran 1997). However, if the surrounding medium is very dense, n 108 cm 3 , Lorentz factors of 1000 can explain the observed short term variability. The immediate conclusion is that in this model GRBs are not caused by mergers of naked compact objects. ski Rather, the required high ambient densities tie this model to the hypernova picture (Paczyn 1998; Woosley 1993), which predicts that the material surrounding the blast is dense because of the pre-hypernova stellar wind. (Dense circum-GRB matter was also suggested in a different context by Katz 1994a).1 The fate of the outer layers of a hypernova precursor is unknown. If the bullets have to travel through a significant fraction of the star’s mantle (which is optically thick and thus not the site where the gamma rays are produced), their opening angle must be extremely narrow: p < 5 10 4 E53 =( N100 3 MM ), where MM is the mass of the mantle in units of M . Since hypernovae are believed to originate from rapidly rotating massive stars collapsing into compact 1 A merger of two compact objects could produce a bullet GRB if the two compact objects were shrouded by a red-giant envelope in a common envelope context. In order to produce the required energies, at least one of these compact objects should be a neutron star or black hole, reducing the likelihood of such an event. 134 objects, it is possible that the material along the rotation axis has collapsed before the GRB, in which case the bullets would travel freely until they hit the circumstellar material. Similarly, little is known about the conditions of the pre-hypernova circumstellar material other than that it must be dense. Massive stars are known to have strong winds with mass 10 6 10 4 Myr 1 and wind velocities from vw 20 km s 1 (red supergiant) to vw 1000 km s 1 (blue supergiant). These winds must still be present after the loss rates of M_ star collapses. In the following, we will assume that the GRB is produced in this leftover wind. The density profile in the ambient matter, then, roughly goes as n /r 2 outside some radius R0 . It is natural to assume that R0 is of the order of the stellar radius, R0 1012 cm for a blue supergiant and R0 1014 cm for a red supergiant. As a conservative estimate we assume that the sphere inside R0 is evacuated. If we parameterize the density as namb(r > R0 ) = where M_ 1:5 1036 cm r2 3 M_ 6 (5.2) v20 6 is the mass loss rate in units of 10 6 M yr 1, r is in cm, and v20 is the wind velocity in units of 20 km s 1 , the observed slowing-down time scale is given by = 0:05 s independent of R0 . E53 v20 4 _ ; 2 2 N100 3 M 6 Thus (5.3) can be of the order of a few milliseconds for both red supergiant and blue supergiant winds if 1000. However, the observed time scale could conceivably be longer than this. The angular smearing time scale ang is defined as the spread in light travel time to the observer across the emitting surface. For a bullet at a viewing angle of gives ang (R0 + R)= E53 v20 =( 3 2 2 2 , which is longer than if 1= this R0 > R= = 1:5 1017 cm _ 6 ). This is only of concern for very dense red supergiant winds, and 100 M 3N only if the region interior to R0 is evacuated. In Fig. 5.3 we show various limits on namb and for a fixed opening angle of 2 = 1: a) Each bullet is expected to plough through undisturbed medium. Thus, the covering fraction N2 of all the bullets together must be smaller than 1. For a slowing down 135 time of 3 = 1, this gives the dashed line in the plot, to the left of which the covering fraction is larger than unity. b) The material between the location where the bullets release their energy and the observer must be optically thin. For 3 = 1 and for R0 = 0 (the most conservative limits) this constraint produces the dash-dotted line to the left of which the optical depth is larger than unity. c) The forward shock must be radiative (see x5.3). This constraint is shown as a light grey region inside of which the shock is not radiative. d) The angular smearing time ang must be smaller than the observed stopping time . This limit is shown as a dotted line for R0 = 1014 cm. To the right of this line, the smearing time is longer than the observed slowing down time. The hatched region in the plot shows how the allowed region of parameter space opens up if we relax the time scale requirements to 3 = 10. It is worth noting that this model makes an exception to the rule that external shocks cannot produce ‘Type II’ behavior (Sari and Piran 1997). This is for two reasons: First, the opening angle of the ejecta is so small that the angular smearing time is short compared to . Second, the ambient density is so high that the observed slowing-down time is 10 3 s. As a result, the total duration of the burst is determined by the time the central engine operates, while the short term variability is determined by the mass of the bullets and the statistical properties of the outflow. This is an important difference from the internal shock model, where the variability timescale is set by the intrinsic time scale of the central engine (e.g., the orbital time in a merger scenario). 5.3 GRB Efficiencies In order for the efficiency of the burst to be reasonable, most of the internal energy pro- duced in the shock must be radiated away immediately (this requirement holds for all GRB 136 104 101 100 10−1 10−2 O Star Wind M˙ −6/v20 102 Red Giant Wind 103 10−3 100 1000 Γ 10000 Figure 5.3: Constraints on the ambient density and for E53 = 1, N100 = 1, and = 0:01. a) covering factor larger than unity: left of dashed line for 3 = 1, dark grey area for 3 = 10. b) optical depth between bullet and observer larger than unity: left of dash-dotted line for 3 = 1, medium grey area for 3 = 10. c) forward shock not radiative: light grey area (we assumed B = 1). d) angular smearing time longer than slowing down time: right of dotted line. The hatched area shows how the allowed region in parameter space expands if we relax the requirement on from 3 = 1 to 3 = 10. models). Electron synchrotron radiation is the only mechanism remotely efficient enough to produce the gamma rays. While the efficiency also depends on the transfer of energy from protons to electrons, we assume here that this process is efficient. Since we know the observed peak frequency of the gamma rays (of order 500 keV , Piran 1999), we can then estimate the radia- tive efficiency under the assumption that the gamma rays are produced by electron synchrotron radiation. It is usually assumed that the magnetic field in the shocked gas is in equipartition with the energy density in relativistic particles. We therefore parameterize the magnetic field strength as UB BUB;eq , where UBeq is the equipartition magnetic field energy density. Since the shocked wind material is likely flowing around the bullets at close to the speed 137 of light (like a cocoon surrounding a radio jet), for efficient cooling we require that the cooling time scale in the comoving frame be smaller than the light travel time across the surface of the bullet (R0 + R)= c. If that were not the case, the material pushed aside by the bullet would cool adiabatically rather than radiatively. Independent of R0 , this translates to the condition p 1430 [M_ 6 22 B=v20 ]1=4 E =500 keV (to the left of the light grey area in Fig. 5.3), where E is the observed peak energy of the gamma rays. This is not a strict condition, however, since we do not know what the efficiency of the GRB is. 5.4 Simulating Lightcurves Since our model assumes a central engine at work (essentially a black box shooting out bullets at a rate R(t)), any distribution of spikes could be reproduced, since R(t) is arbitrary. It is, however, surprisingly simple to reproduce the main features seen in different burst profiles by varying only a few parameters in our model. For simplicity, we assume that all the bullets have the same initial and the same sideways expansion rate, i.e., constant . We are left with two parameters — the number of bullets N100 and the average slowing-down time (eq. [5.3]) — and two unknown functions: the mass distribution of the bullets N (Mb ) and the rate at which they are released R(t). We assume that N (Mb ) / Mb 1=3 , chosen to give the observed power spectrum of P ( ) / 1=3 (Beloborodov et al. 1998). For R(t) we assume (for lack of better knowledge) that the bullets are released randomly over a time interval of 15 sec. To produce synthetic GRB lightcurves, we calculated the time dependence of and the associated dissipation rate. Assuming the bullets are radiating efficiently and correcting for Doppler boosting and frequency shifts, we then computed the composite lightcurve for each bullet. We have plotted two simulated light curves in Fig. 5.4 for 3 c) and N = 104 (panel d). It seems that simply by varying N100 = 10 and N = 100 (panel and 3 we can produce a wide range in light curve shapes. More complex features (like the gaps seen in panel a) must be related to the activity of the central engine and cannot be reproduced by a random spike rate as assumed above. We have also plotted the light curve produced by the deceleration of a single 138 BATSE count rate [arbitrary units] a) 0 b) 10 20 30 40 0 c) 0 5 10 15 5 10 15 20 d) 5 10 15 20 0 t [sec] 20 Figure 5.4: BATSE light curves for GRB920627 (panel a) and GRB980329 (panel b) and two synthetic light curves. These curves were calculated for a burst duration of 15 s, a mass distribution of N (Mb ) / Mb 1=3 , an average slowing down time of = 0:01 s, and N100 = 1 (panel c), N100 = 100 (panel d). The insert in panel c shows a template light curve for a single shot. bullet along the line of sight (Fig. 5.4c, insert). Note that this profile is very similar to a true FRED (fast rise, exponential decay) profile. The rise is instantaneous and the decay follows a steep power-law (to first order). While indicative, these calculations are still rather crude and simplistic. A more careful analysis of shotgun GRB lightcurves should be carried out in the near future. 5.5 Afterglows in the Shotgun Model Afterglows are an important test for any GRB model. How can we understand an after- glow in the context of the shotgun model? It is not immediately obvious why our model should produce an afterglow at all. This is because the bullets are assumed to spread sideways. As mentioned above, the bullets will have lost half of their kinetic energy at R, where they have swept up 1= of their own mass. If we simply followed the dynamics of an individual bullet 139 further in time, it would lose the rest of its energy exponentially quickly (Rhoads 1997). This is because the sideways velocity in the lab frame goes as 1= , so that when starts decreasing, the sideways velocity increases, which in turn increases the cross-sectional area of the bullet. As a result, the bullet can sweep up more mass, which leads to a run-away process. This would imply that the ejecta would come to a complete stop not far away from R and the observed afterglow would last less than a day. However, there are many bullets traveling together. As they expand, they start increasing the covering factor of the blast. Once the collection of bullets reaches unit covering factor, they stop slowing down exponentially, since further sideways expansion does not lead to an increase in swept up mass. As a result, the bullets start traveling collectively, resembling a collimated blast wave with opening angle rather than a meteor shower. The only possible difference between our model and the standard afterglow models is that in our model, the external density follows a power-law behavior instead of being constant, which has been discussed by Dai and Lu (1998). Since the opening angle of the merged blast is much larger than the opening angle of the individual bullets, the sideways expansion does not affect the dynamics until much later, when the blast has spread by an angle of order (Rhoads 1997). This transition from constant opening angle to rapid sideways expansion has been used in other models to explain the temporal break seen in the afterglow lightcurve of GRB990510 (Stanek et al. 1999; Harrison et al. 1999; Sari et al. 1999). 5.6 Making Bullets Having established that the bullet model can indeed explain the observational signatures of GRBs, we now turn to the question of how these bullets are produced. This is a far more complicated problem to solve and here we will only outline avenues that might be taken in more depth in future research. The typical bullet mass that must be produced by any such model is given by M 10 13 ME53=( 4 N100 ), while the size of the bullets is only 1010 cm. Both of the approaches outlined here start from a common fireball scenario. It is therefore 140 worthwhile to review the properties of a stationary fireball type wind. Such a wind corresponds to a simple adiabatic spherical wind. For the sake of simplicity, we assume that the flow is ultra-relativistic in the observer’s frame. The conservation of energy and momentum flux (here, no sideways transport of momentum can occur, since the flow fills 4 sterrad) read 2v c2 + 4p r2 = const: (5.4) and 2 v2 c2 + 4p r2 + 2 pr2 = const: In the limit of v 2 r2 p (5.5) c, p c2 , this translates to const: (5.6) The equation of state can now be written (see x2) p/ 4=3 r 8=3 (5.7) and the solution is simply / r; p / r 4: (5.8) Thus, in an idealized fireball, the Lorentz factor grows linearly with r until the flow reaches c2 p, at which point the flow turns cold and no more internal energy is available for acceleration. At this point the flow has reached its terminal Lorentz factor, 1 3p0=0 c2 . The subscript 0 denotes quantities evaluated at the injection point. It is clear from this that the ratio of rest mass energy density to pressure determines 1. Since the rest mass density is domi- nated by baryons, it is the baryon fraction rather than the total particle density that determines the Lorentz factor of the flow. Since GRBs are assumed to have 1 100 1000, the baryon fraction in the flow must be small. Since the problem of achieving low baryon loading concerns every GRB model and is the topic of ongoing research, we will simply assume that such a low baryon fraction can be established and proceed from there. 141 The acceleration measured by a comoving observer (after a little algebra) is simply given by a = c3 @ v@r c2=r0 ; (5.9) where r0 is the injection radius. Thus, the comoving observer feels constant acceleration, which makes treatment conveniently simple. Having established these key relationships, we can look at the first possibility for bullet production. 5.6.1 Why Bullets Must be Contained by Adiabatic Compression One might ask if it is possible to start out with a flow that has uniform density but non- uniform types of pressure, e.g., mostly photons in one region and magnetic fields in another. In such a case, it might be possible for the radiation to leak out of the radiation-dominated region in a photon diffusion time. The exterior magnetic pressure would then squeeze the now underpressured region, creating a density contrast, which can essentially be described as a bullet. However, for a bullet of mass pairs, is T Mb 10 13 M the optical depth, even neglecting 1010 =R52 , where R5 is the bullet radius in units of 105 cm so the bullets are still optically thick even when they slow down, and the radiative diffusion time is much longer than the travel time of the bullet. Unless the conditions in the flow are different than what is typically assumed to make the flow optically thin, it is not possible to create bullets by squeezing radiation out of them. Thus, any compression of these bullets must be adiabatic. There is one exception, though: if the fireball is hot enough, the rapid establishment of pair equilibrium will lead to a high rate of neutrino production from pair annihilation. While the entire flow is highly optically thick to photons when it is launched (i.e., a few tens of gravitational radii away from the central engine), under certain conditions it is still optically thin to neutrinos. The optical depth of the entire fireball to neutrinos is 2 10 7 E53 r7 t10 (5.10) 142 while the neutrino emissivity is given by 7:82 1025 E53 9=4 ergs cm 3 s t10 r7 2 1 (5.11) Note that pair annihilation dominates over pair capture neutrinos for the conditions encountered in GRBs, which is why we can neglect the baryon density in this expression. Thus, if a region exists that is hotter than its environment, most likely due to higher photon pressure and lower magnetic field pressure, it can cool rapidly and compress significantly before cooling adiabatically due to the expansion of the flow if the neutrino cooling rate satisfies U < r=c = 3:3 10 4 r7 ; (5.12) where U is the energy density in the fireball. This can be translated into an energy requirement: E53 > 1:6 103 r76=5 t10 (5.13) It is interesting to note that fireballs are neutrino cooled for isotropic energies in the range 1:6 103 r7 6=5 t10 < E53 < 5 106 r7 t10 (5.14) where the upper limit is given by the condition that the fireball be optically thin to neutrinos. Thus, if the total burst energy falls within that range, the fireball will cool rapidly until the energy falls below that threshold, i.e., the total isotropic energy of the actual GRB is limited to 1:6 1056 ergs s 1 r7 6=5 t10 . Note that this argument is independent on whether the burst is isotropic or not because it only depends on the thermodynamic state of the plasma. In a sense, then, GRBs could be regarded as standard candles since their luminosities seem to be limited from above, and determining the luminosity envelope as a function of redshift could be used to complement SN 1a observations. In reverse, we can use a large observed burst energy to set a lower limit on the injection radius. Since GRB efficiencies are poorly understood, these limits are so far uninterestingly low. 143 5.6.2 Rayleigh-Taylor Driven Bullet Formation The inherent assumption about the internal shock model is that the flow is not stationary, but rather highly variable, with different epochs of the fireball having different baryon loading. Here we wish to investigate the effects of Rayleigh Taylor instability on a fireball with abrupt changes in rest mass density, as might occur in an internal shock scenario. All the groundwork for this has been laid in the previous paragraphs and Appendix C. Once again we write the isotropic energy released by the GRB as and the time scale over which this release takes place as t = 10 t10 sec. E E53 1053 ergs Without loss of gen- erality we can assume that the burst is isotropic, as long as the opening angle of the entire outflow is larger than the beaming angle of the flow after it reaches terminal velocity. We parameterize the injection radius as 10M black hole is Rgrav r = 107 r7 cm. 1:5 106 cm. p 1026 ergs cm 3 E53 t10 1 r7 Note that the gravitational radius of a The pressure inside the fireball is then given by 2. We now assume that a contact discontinuity exists in the flow, with the rest mass density higher on the side further away from the central engine. Taking the surface to be perpendicular to the direction of motion, and keeping in mind that the flow is accelerating, this corresponds to a heavier fluid sitting on top of a lighter fluid, which is the classical condition for RayleighTaylor instability to occur. For the sake of simplicity, we will neglect the curvature of the interface, thus the analysis from Appendix C directly applies. The densities on either side of the interface are the last parameter necessary. We know that GRBs reach 100 1000, so 0 3p=100 3p=1000 and we assume a density contrast of order 10 between the two shells. It is clear from the dispersion relation that Rayleigh-Taylor instability is weakened in relativistic gases, since the inertia is given by the enthalpy rather than just the rest mass density, but since both sides of the interface must be in pressure balance, no additional buoyancy effects arise. In other words: the stabilizing inertia is increased, while the de-stabilizing force is not. Why, then, one might ask, should Rayleigh-Taylor instability be of importance in GRBs, where 144 the plasma starts out highly relativistic. The answer lies in the enormous acceleration felt by the plasma: in the comoving frame, the acceleration is given by a 9 1013 cm sec 2 ; r7 (5.15) quite large compared to any acceleration encountered in most other places in the universe, larger than the typical acceleration at the base of AGN jets by the inverse ratio of the black hole masses involved, roughly 105 108 . It is well known that the fastest growth rates for non-magnetic Rayleigh-Taylor instability without surface tension are found at the shortest wavelengths. However, we are interested in the modes that contain the most mass and can still grow during the time the flow accelerates. An important requirement on any growing mode is that it stay in causal contact during the entire acceleration phase, which will put an upper limit on the wavelength. To calculate the growth time for a given mode, we integrate the inverse growth rate over the acceleration time of the flow. In order to take account of the sideways expansion of the flow, we scaled the wavelength with r, in other words, k(r) = k0 (r0 =r). The integration was done numerically and the results are shown in Fig.5.5. We can see that the most massive bullets fit well with the masses we inferred in the previous sections. Once the instability has become non-linear, the heavy fluid will fall behind in the form of fingers, which would be rather similar to the bullets we are looking for. As we can see, the most massive bullets are contained in the largest wavelengths. Since the flow keeps expanding sideways even after acceleration terminates, we still have to contain the bullets, otherwise they would spread and be much larger than what is needed for the shotgun model to work. The next section will outline a method how confinement can be established. However, this method can work to produce bullets even in the absence of Rayleigh-Taylor instability. The purpose of the previous analysis was simply to show that spherical symmetry in a standard internal shock scenario is likely to be broken, producing clumps of matter that contain mass on the scales 145 Mb [g] 1020 1019 10 z/z0 Figure 5.5: Mass enclosed in the longest wavelength mode that has grown non-linear as a function of distance from the core for r7 = 1 and 1 = 1000. expected in GRBs. 5.6.3 Ram Pressure Confinement and Acceleration The so called plasmon model was the first approach at explaining radio galaxies. It was envisioned that the radio lobes were blobs of relativistic plasma that were ejected from the nucleus in opposite directions and were subsequently interacting with the ISM. The ISM would then decelerate the blobs and at the same time confine them through ram pressure (see Christiansen 1969, for details). Even though this picture has long since been discarded in favor of the jet/lobe paradigm, it might be of interest in the context of GRB bullets, as we will show in the following. If a blob of gas of a given mass Mb is embedded in a stream of gas that has a relative velocity vrel with respect to it, the blob will experience a ram pressure from that flow that will act to accelerate it in order to decrease the relative velocity of the blob with respect to the flow. 146 background scale height bullet radius background flow contact discontinuity bullet scale height bullet acceleration α bow shock static pressure + ram pressure Figure 5.6: Cartoon of bullet acceleration by ram pressure. The bullet is shown in red, the background flow in blue, and the shocked material confining the bullet is shown in yellow. Also shown are bullet radius and bullet scale height (roughly equal) and the background scale height (not necessarily the same). At any given point at the surface the ram pressure will be given by pram = hf 2 2 2 rel vrel cos ; (5.16) where is the angle of incidence of the flow, i.e., the angle between v and the surface normal (see Figure 5.6 for illustration), rel is the relative Lorentz factor between blob and background flow, measured in the frame of the blob, and hf the enthalpy in the background flow. Force balance across the blob surface will lead the shape of the blob to change until it reaches pressure equilibrium between ram pressure, internal bullet pressure, and the static pressure in the background flow. Since the blob is accelerated, its internal pressure must be stratified, with a scale height 147 of b = pb =(gb hb ), d ln pb (z ) = 1=b dz (5.17) where cb is the internal sound speed and gb its acceleration. If the background flow is accelerating, it too must be stratified, with a different scale height than the blob, f . The pressure balance condition then reads: pb (z ) = pf (z ) + hf (z ) 2 v2 cos2 (5.18) This situation is illustrated in Fig.5.6. Using " dR dR cos = 1+ dz dz 2 # 1=2 (5.19) we can write equation 5.18 as v dR u 1 t 2 2 =u v h f dz p p b 1 f : (5.20) While equation 5.20 cannot be solved analytically, one can show that in the limit pram pf ;0 (i.e., negligible static pressure in the external flow) an approximate solution can be found (Christiansen 1969) with R b f f b b; (5.21) in the case of an internally isothermal bullet, or R 2:4 b f f b pb 2:4b 2:4 ah ; b for an adiabatic bullet. This is of the same order as the blob scale height (we expect f (5.22) > b since the blob is compressed by ram pressure). Thus, as it turns out, the blob will be roughly spherical in shape. Even if pf is not negligible, the sideways dimension of the blob will be comparable to the scale height as long as pram is comparable to pf . For the case where pf is much larger than pram the blob shape will not be altered by ram pressure effects from its original shape, but in this case the blob acceleration will also be small. If the background flow is accelerating itself, pram will eventually catch up with pf . Since the surface area of the blob 148 is known, the acceleration of the blob can be calculated from the momentum flux through that surface. This determines the dynamics of the blob completely: the acceleration of the bullet (in the ultra-relativistic limit) is given by d b pramRb 2 = ; dr hb Vb (5.23) where Vb is the bullet volume and hb Vb is the bullet inertia. Since Rb and Vb both depend on the acceleration through equation 5.20, this is a system of coupled equations, which can, in general, only be solved numerically. 5.6.3.1 Bullet Acceleration In the standard fireball model it is inherently assumed that the initial fireball is homogeneous, i.e., the baryon density is the same everywhere. This assumption is relaxed in the internal shock model, where the baryon density varies as a function of time, but is constant on shells of constant r at least within areas larger than the beaming angle. It is no surprise that such a setup cannot give rise to bullets. There is, however, no reason to assume that the isotropy of the fireball cannot be broken on smaller scales. It is quite plausible to assume that a distribution of baryon densities exists in regions of different sizes. For simplicity, we will assume in the following that the initial fireball contains overdense roughly spherical regions of a given size RB , not unlike raisins in a cake batter. In such a case, a hierarchical acceleration scenario will unfold: As long as the entire flow is relativistic, it will accelerate in unison following the linear acceleration phase outlined above. The overdense regions will become non-relativistic first and will start lagging behind with respect to the background flow. This will induce ram pressure acceleration and confinement. This ram pressure acceleration will continue until the bullets reach a significant fraction of the speed in the background flow or until they encounter the stationary ISM. Since the pressure inside the blob is enhanced over the static pressure in the background flow, they expand at a slower rate 149 than the background flow. This provides confinement. We write the initial radius of the overdense region at the base of the flow as R5 105 cm. This is the initial bullet size at the base of the flow, i.e., at r = r0 . R0 = After accelerating with the flow, the bullet will become rest-mass dominated when b c2 > 3pb . the initial bullet density is b;0 and the initial bullet and background pressure is pb;0 = p0 , this happens at a distance rc If 3p0=0 r0 , where = rc =r0 . At this point the background flow is still relativistic, and the size of the bullet is now Rc = R0 rc =r0 . At the base of the flow the scale height in bullet and background gas are the same, b = f . Throughout the linear acceleration phase of the bullet, this will continue to be the case, since during this phase the rest mass density is dynamically unimportant. The scale height of the background flow measured in the frame of the bullet is f = b dppff =dr = r0 =4. The bullet Lorentz factor enters through the Lorentz contraction from observer’s scale height to bullet scale height. The bullet starts out much smaller than its own scale height (otherwise it would be out of casual contact) and when it reaches rc it should still be smaller or of the same order as b (again, it must still be in causal contact). If the bullet size Rc at rc is similar to b then the ram-pressure acceleration model discussed above directly applies and we can simply integrate the equations to the point where the bullets hit the ISM. If the bullet size is smaller than b when it slows down, it will have to adjust to the Christiansen solution discussed above. The bullet has to stay in pressure equilibrium with its environment at all times, which (by equation 5.18) translates into an intermediate relation between bullet size Rb and its scale height, which will be valid for R < b . For an internally isothermal bullet, this can be written as b = Rb : ln (1 + pram=pf ) + Rfb (5.24) The bullet behaves adiabatically, implying a relation between bullet pressure and radius R. The bullet acceleration is determined through it scale height simply by a = cs 2 =, where a 150 is the bullet acceleration measured in the bullet frame and cs 2 = ad p=h is the sound speed in the bullet. Once the bullet size reaches b the Christiansen model can be used. As stated above, these equations will have to be integrated numerically, but in the case where Rc b we can do the integration analytically. Ram pressure confinement gives Rb = where ad p cs 2 = 2 ad b ; 2 c d b =dr b c d b =dr (5.25) = 4=3, since the bullet is optically thick and thus radiation pressure dominated. The bullet behaves adiabatically, thus pb / R 4 ; b / R 3 : (5.26) Together with equation 5.25 this gives s 2:4pb;c ; b;c c2 d b =dr (5.27) 2:4pb pb;c R; Mb c2 b;c c2 c (5.28) R = Rc and d b = dr s where Mb is the bullet mass. We assume that pram > pf so that pb pram. The ram pressure in the bullet frame is given by 2 2 rel vrel : pram = hf (5.29) We assume that the relative velocity between bullet and background flow is already relativistic, so that rel pram / f b 1. In that case, we have the proportionality relation 1 2 : b r2 (5.30) Note that this relation is valid both for accelerating and coasting background flow: in the accelerating phase, hf f 4pf =c2 / r 4 and f / r2, while in the coasting case hf f / r 2 and = const. With this the equation of motion becomes d b = dr r 3 2:4 pb;c rc 4 b;c c2 Rc r b;c ; b (5.31) 151 which has the solution b = v u u t2 s b;c 3 2:4 4 1=2 3 2:4 4 pc rc r ln b;c c2 Rc rc r7 r = 100 ln : b;c R5 rc The ram pressure as a function of r is simply pram pram;c(rc 2 3 1=2 bullet behaves adiabatically and pb Rb = Rb;c pram;c pram 1=4 (5.32) 2 b;c =r b ) , and since the pram, we have s = Rb;c r rc b : b ;c (5.33) Since b only grows logarithmically beyond rc , the bullet is well collimated and even initially very large bullets will be small enough to satisfy the size constraints in the bullet model. As was mentioned above, a key constraint on this model is that the bullet stay in causal contact throughout acceleration and collimation phase. Since the bullet expansion is very slow beyond rc , the strongest constraint on the bullet size is that it be in causal contact at rc , i.e., Rc < rc= b;c , which translates to R5 < r7100= b;c = r7 100 b;0 c2 : 3 p0 (5.34) If the bullet were to become causally disconnected, the ram pressure collimation mechanism would not be able to act on the entire bullet. Instead, the bullet would be compressed in the direction of motion to become oblate and then break apart into units roughly the size of a causally connected patch. The longitudinal collapse of the bullet would presumably occur in a shock, since the bullet is not causally connected longitudinally either when it reaches rc . This would correspond to an internal shock, since most of the energy goes into heating the bullet rather than accelerating it. It is therefore possible that the internal shock model and the shotgun model co-exist. The causality requirement can be translated into an efficiency estimate. Equation 5.34 tells us that the largest bullet possible satisfies b;c such a bullet boosts b to b;ISM 3:2 s c ln 100r7 =R5 . Ram pressure acceleration for rISM 109 cm : 1014 cm rc (5.35) 152 where rISM is the location where the ISM starts slowing down the bullets. The mass in the bullet is Mb = 4=3R0 3 b;0 = 4=3R5 3 1015 cm3 3p0 = c c2 and its kinetic energy when it reaches the ISM is Ekin Mb (5.36) 2 b;ISM c . If the number of bullets within the beaming angle is 100N100 , then the total energy in the bullets is Ebullets = 400N100 b 3 M c2 ; b (5.37) while the total energy in the fireball is Ereball 12 1015 c p0 r7 2 t10 cm2 s = 1053 p0 r 2 t ergs: 26 10 dyn 7 10 (5.38) The total efficiency of the burst, defined as the kinetic energy in bullets divided by the total energy in the fireball, is burst Ekin;bullets Ereball 1 N100 R5 680 : t (5.39) 10 We note that the efficiency of the burst decreases if the bullets are smaller than the maximally causal size assumed in this analysis. Since the energy efficiency is mostly determined by the filling factor of the bullets, a smaller bullet size would imply a larger number of bullets to satisfy reasonable efficiency limits. Note that the acceleration is somewhat more efficient in this case, since the bullet must adjust to the Christiansen solution first. Detailed numerical simulations are needed to solve this problem self-consistently. 1. Equation 5.39 shows that for the bullet efficiency to be high we need N100 R5 =t10 While r7 does not enter into the efficiency, it does determine b;c , and thus the terminal the bullets. Since we require the bullets to have spikes, increasing of 1000 in order to produce millisecond type R5 implies increasing r7 if the bullets are to stay in causal contact. Large injection radii are difficult to reconcile with the idea that the GRB is produced close to the horizon of the central black hole. Increasing the number of bullets much beyond N100 also difficult to justify. 10 is 153 It thus seems that the region of parameter space where ram pressure acceleration can produce GRBs is very restricted. We note, however, that not all GRBs display millisecond timescale variability, which relaxes the requirements on and N100 somewhat. Furthermore, some GRBs show both smooth, relatively long lasting sub-structure and spikes (e.g., GRB 980425 and 990123, see Figure 1.5). In such cases, the smooth sub-structure might be produced by the background flow in an ordinary external shock scenario while the spikes are produced by bullets in the flow. This would lower the required efficiency for the burst, since most of the energy could reside in the background flow. Finally, these estimates are still very crude. Since the terminal bullet Lorentz factor b enters into the efficiency to the third power, estimates of b are crucial in determining and more detailed calculations are needed before any definite conclusions about the viability of ram pressure acceleration can be drawn. Another important issue to consider is the effect of KelvinHelmholtz instability, which might act to disrupt the bullet before it reaches the ISM. Future work will focus on these questions. 5.7 Chapter Summary This Chapter presented a GRB model based on the shocks that small blobs of rela- tivistically moving material drive into the dense atmosphere of hypernova progenitors. The lightcurves produced by such bursts are consistent with the shape and variability seen in BATSE lightcurves. Afterglows fit naturally within this picture, as bullets merge at the end of the GRB phase and form a common shock front. We find that bursts with satisfactory efficiencies (of order injection radius is larger than generally assumed, i.e., r7 imply b;c 0:1) can be achieved if the > 10, in which case R5 > 5 would not 100. Bullet numbers in the range of N100 10 are also within reasonable limits. We have shown that bullet production via ram pressure acceleration is possible, though rather restrictive in the parameter ranges possible. More research is necessary to evaluate the effects of magnetic fields and to solve the equations of motion completely self-consistently. Chapter 6 Conclusions This thesis investigated the physics of relativistic outflows encountered in AGNs and GRBs. Jets are a ubiquitous phenomenon in astrophysical scenarios, yet the production and collimation of jets are still open issues and the interal makeup of jets is unknown. Due to their cosmological distances and small angular sizes, GRBs are even less well understood. The second chapter presented a simple analytic model of jet acceleration. The jet is accelerated by tangled magnetic fields, with collimation being provided by pressure from an external medium. Using tangled fields as a jet acceleration mechanism is a new approach, based on B95, as previous models of MHD jet acceleration concentrated mostly on large scale organized fields (though tangled field evolution in a more general context and under somewhat different conditions has been considered extensively, e.g. Goldreich and Sridhar 1997). Our analytical quasi-1D approach is limited to narrow jets, for which the opening angle is smaller than the beaming angle, coincident with the condition that the jet be in causal contact with its environment. We introduced an ad-hoc process that redistributes energy between perpendicular and parallel field to facilitate efficient conversion of internal energy to kinetic energy. Without such a process, stationary jet acceleration by disorganized fields is impossible. In the absence of dissipation, the rate of acceleration achieved under this scenario is the same as in the case of relativistic particle pressure, / pext 1=4 . We also found analytic solutions beyond the self-similar region, which enable us to calculate the terminal bulk Lorentz factors of such jets. In order for these jets to reach the observed > 10, they must be magnetically dominated at 155 early stages. We estimated the impact of dissipation of magnetic energy on the dynamics of the flow by considering a simple, phenomenological prescription of the loss process. The presence of dissipation lowers the terminal Lorentz factor 1 and generally changes the rate at which the jet is accelerated (the latter effect is noticeable only if the dissipation rate is comparable to the adiabatic expansion rate). We also included the effects of radiation drag in the simplest scenario, which always lowers the efficiency and 1. The amount of radiation drag in our model is controlled by the amount of dissipation replenishing the high energy particle pool but seems to be dynamically unimportant. We calculated the frequency integrated surface brightness for the extreme cases where all or very little of the dissipated energy is radiated away on the spot and found that, while the brightness drops off very rapidly in all considered cases due to the expansion of the jet, values of the dissipation efficiency > 0:05 can have a significant impact on the intensity as a function of z . In the marginally non-radiative case, the build-up of particle energy leads to a slower decline in intensity with z for larger . Finally, we applied this model to the prototypical radio galaxy M87 and found that it is consistent with the observed properties. It should be noted again that this model is a gross oversimplication. In reality, it is likely that the field will contain both ordered and chaotic regions, and a combination of the two associated models seems most appropriate. This work should thus be regarded as only a first step towards an integrated picture. In the third chapter, we investigated the energetics of jets, concentrating on the best studied example available, the jet in M87. We proposed that the apparent lack of synchrotron cooling in the M87 jet most likely indicates the presence of a sub-equipartition magnetic field. While the total (particle + magnetic) pressure needed to explain the observed synchrotron emissivity is uncomfortably high in the nonrelativistic limit, Doppler beaming effects consistent with bulk Lorentz factors in the range 2 5 lower the pressure requirements considerably. Fluctu- ations in the synchrotron emissivity and spectral cutoff frequency are consistent with adiabatic 156 changes in the magnetic field strength and particle energies that accompany compressions and rarefactions along the flow, and Fermi acceleration along the flow is not necessary to explain the observations. The knots are identified with relatively weak shocks, as inferred from other data by BB. The first-order Fermi acceleration expected to occur at such shocks, if any, would generate a particle energy distribution steeper than the n(E ) / E 2 needed to produce the radio–to–optical synchrotron spectrum. Thus, effects of particle acceleration along the jet might be apparent only shortward of the cutoff frequency, e.g., in the X-ray band. However, a disordered magnetic field or a “superluminal” field orientation with respect to the shock front (Begelman and Kirk 1990) could further reduce the efficiency of Fermi acceleration, hence we should continue to regard the origin of the X-ray emission as unknown. The pressure estimates we derive are consistent with the assumption that the M87 jet is embedded in a moderately overpressured bubble, as suggested by BB. As a result, it seems that the set of parameters we have suggested above can solve the cooling problem of the M87 jet, as sub-equipartition fields are able to explain both the behavior of the cutoff frequency and the confinement of the jet. Using derived values for the magnetic field and the cutoff momentum at r0 we can put an upper limit of 10 pc on the radius at which most of the particle acceleration occurs. Explaining why the acceleration is confined to a particular scale (which may be quite large compared to the size of the central black hole) poses an interesting problem for future work. The analysis of the M87 jet we carried out could be improved by better deprojection models of the jet. Higher quality spectral data both in the near infrared and the X-ray will help to verify the assumption of constancy of the underlying spectral shape and decrease the uncertainty in the location of spectral features (the knowledge of which is essential for this technique to work). The community is still awaiting the publication of the HST/NICMOS and the Chandra results. Given the fact that M87 is a relatively weak source, it would be very interesting to in- 157 vestigate other sources to see if the results derived above carry over. Such an effort is now underway: we are participating in a broad band radio/optical/UV campaign of several nearby AGN jets, which will hopefully be extended to X-ray energies in Chandra Cycle 2. The techniques outlined in chapter 2 should be very useful in analyzing these jets. Chapter 4 presented a simple model for the evolution of powerful radio galaxies into a surrounding ISM/ICM in order to make predictions about the detectability and appearance of such sources for future X–ray missions. We assumed uniform pressure, spherical symmetry, and a King profile density distribution in the ambient medium to describe the cocoon and the shell of swept-up material and have calculated a grid of models for various source parameters to provide observational diagnostics for high resolution X–ray observations. We are particularly interested in young sources, since signatures of intermittency are most pronounced in the early stages of source evolution. However, there is only a rather limited range of parameters for which we might hope to detect the shell of such sources, since the expected count rates are low for all but the most dense environments. Also, contamination by a bright core could make such detections impossible. Larger sources offer more chances not only for detection but also for analysis and application of our model grid. For a source with known redshift and core radius, it should be possible, at least in principle, to determine the central density of the King profile, the average kinetic source luminosity, and the source age. The knowledge of these parameters could help a great deal in understanding the process of jet formation. As an example we apply our model to a 50 ksec ROSAT HRI observation of Perseus A, and find that the time averaged power most likely exceeds 1045 ergs sec 1 . We have shown that GRBs can be produced by a shower of cold, heavy bullets shot at bulk Lorentz factor 1000 into a dense medium. The required densities are consistent with a stellar wind from either a blue or red supergiant, which ties our model to the hypernova scenario. The gamma rays are produced by the shocks these bullets drive into the ambient gas. The total duration of the burst is then determined by the time the central engine operates rather than the 158 slowing-down time of the bullets, while the latter produces the short-term variability seen in many bursts. After the gamma ray phase (when the bullets have lost half of their kinetic energy to radiation) the blast waves of the individual bullets merge into a single collimated shock front, which produces a standard afterglow in a declining external density profile. One possible creation mechanism for such bullets is ram pressure acceleration and collimation. The seeds for the bullets can either be provided by an inherently inhomogeneous, non-isotropic fireball or, by Rayleigh-Taylor instability of onion-shell like internal shock fireballs. Both mechanisms could occur in the standard hypernova scenarios commonly envisioned as possible central engines for ordinary internal shock GRB models. Bibliography Akerlof, C. et al. (1999), ‘Observation of Contemporaneous Optical Radiation from a GammaRay Burst’, Nature, 398, 400. Allen, A. J. and Hughes, P. A. (1984), ‘The Rayleigh-Taylor Instability in Astrophysical Fluids’, MNRAS, 208, 609. Allen, S. W., Fabian, A. C., Edge, A. C., Böhringer, H., and White, D. A. (1995), ‘Cooling Flows, Central Galaxy-Cluster Alignments, X-ray Absorption and Dust’, MNRAS, 275, 741. Antonucci, R. R. J. and Miller, J. S. (1985), ‘Spectropolarimetry and the Nature of NGC 1068’, ApJ, 297, 621. Baade, W. (1956), ‘Polarization in the Jet of Messier 87’, ApJ, 123, 550. Balbus, S. A. and Hawley, J. F. (1991), ‘A Powerful Local Shear Instability in Weakly Magnetized Disks. I - Linear Analysis. II - Nonlinear Evolution’, ApJ, 376, 214. Ballard, K. R. and Heavens, A. F. (1992), ‘Shock Acceleration and Steep-Spectrum Synchrotron Sources’, MNRAS, 259, 89. Begelman, M. C. (1995), ‘The Acceleration and Collimation of Jets’, Proc. Natl. Acad. Sci., 92, 11442, B95. Begelman, M. C. (1996), ‘Baby Cygnus A’s’, in Cygnus A: Study of a Radio Galaxy, Carilli, C. L. and Harris, D. E. (eds.), page 209, Cambridge: Cambridge University Press. Begelman, M. C. (1998), ‘Instability of Toroidal Magnetic Fields in Jets and Plerions’, ApJ, 493, 291. Begelman, M. C. and Cioffi, D. F. (1989), ‘Overpressured Cocoons in Extragalactic Radio Sources’, ApJ, 345. Begelman, M. C. and Kirk, J. G. (1990), ‘Shock-Drift Particle Acceleration in Superluminal Shocks - A Model for Hot Spots in Extragalactic Radio Sources’, ApJ, 353, 66. Begelman, M. C. and Li, Z. Y. (1994), ‘Asymptotic Domination of Cold Relativistic MHD Winds by Kinetic Energy Flux’, ApJ, 426, 269. Beloborodov, A. M., Stern, B. E., and Svensson, R. (1998), ‘Self-Similar Temporal Behavior of Gamma-Ray Bursts’, ApJ, 508, L25. 160 Bicknell, G. V. and Begelman, M. C. (1996), ‘Understanding the Kiloparsec-Scale Structure of M87’, ApJ, 467, 597, BB. Bicknell, G. V., Dopita, M. A., and O’Dea, C. P. (1997), ‘Unification of the Radio and Optical Properties of Gigahertz Peak Spectrum and Compact Steep-Spectrum Radio Sources’, ApJ, 485, 597. Biretta, J. A. (1993), ‘The M87 Jet’, in Astrophysical Jets, Burgarella, D., Livio, M., and O’Dea, C. (eds.), volume 6 of Space Telescope Science Institute Symposium Series, page 263, Cambridge: Cambridge University Press. Biretta, J. A. and Meisenheimer, K. (1993), ‘The Jet of M87’, in Jets in Extragalactic Radio Sources, Röser, H.J. and Meisenheimer, K. (eds.), volume 421 of Lecture Notes in Physics, page 159, Berlin: Springer. Biretta, J. A., Sparks, W. B., and Macchetto, F. (1999), ‘Hubble Space Telescope Observations of Superluminal Motion in the M87 Jet’, ApJ, 520, 621. Biretta, J. A., Stern, C. P., and Harris, D. E. (1991), ‘The radio to X-ray spectrum of the M87 jet and nucleus’, AJ, 101, 1632. Biretta, J. A., Zhou, F., and Owen, F. N. (1995), ‘Detection of Proper Motions in the M87 Jet’, ApJ, 447, 582. Blackman, E. G., Yi, I., and Field, G. B. (1996), ‘Relativistic Precessing Jets and Cosmological Gamma-Ray Bursts’, ApJ, 473, L79. Blandford, R. D. and Begelman, M. C. (1999), ‘On the Fate of Gas Accreting at a Low Rate on to a Black Hole”’, MNRAS, 303, L1. Blandford, R. D. and McKee, C. F. (1976), ‘Fluid Dynamics of Relativistic Blast Waves’, Physics of Fluids, 19, 1130. Blandford, R. D. and Payne, D. G. (1982), ‘Hydromagnetic Flows from Accretion Discs and the Production of Radio Jets’, MNRAS, 199, 883. Blandford, R. D. and Rees, M. J. (1974), ‘A ‘Twin-Exhaust’ Model for Double Radio Sources’, MNRAS, 169, 395, BR. Blandford, R. D. and Znajek, R. L. (1977), ‘Electromagnetic Extraction of Energy from Kerr Black Holes’, MNRAS, 179, 433. Bloom, J. S. et al. (1999), ‘The Host Galaxy of GRB 990123’, ApJ, 518, L1. Böhringer, H., Voges, W., Fabian, A. C., Edge, A. C., and Neumann, D. M. (1993), ‘A ROSAT HRI Study of the Interaction of the X-ray-Emitting Gas and Radio Lobes of NGC 1275’, MNRAS, 264, L25. Boksenberg, A. et al. (1992), ‘Faint Object Camera Observations of M87 - The Jet and Nucleus’, A&A, 261, 393. Brooks, M. Spaceballs. movie, 1987. 161 Buote, D. A. (2000), ‘Oxygen Absorption in Cooling Flows’, ApJ, 532, L113. Camenzind, M. (1986), ‘Centrifugally Driven MHD-Winds in Active Galactic Nuclei’, A&A, 156, 137. Carilli, C. L., Perley, R. A., and Harris, D. E. (1994), ‘Observations of Interaction Between Cluster Gas and the Radio Lobes of Cygnus-A’, MNRAS, 270, 173. Chandrasekhar, S. (1961), Hydrodynamic and Hydromagnetic Instability, Oxford, Clarendon Press. Chartas, G., Worrall, D. M., Birkinshaw, M., Cresitello-Dittmar, M., Cui, W., Ghosh, K. K., Harris, D. E., Hooper, E. J., Jauncey, D. L., Kim, D. W., Lovell, J., Marshall, H. L., Mathur, S., Schwartz, D. A., Tingay, S. J., Virani, S. N., and Wilkes, B. J. (2000), ‘The Chandra X-ray Observatory Resolves the X-Ray Morphology and Spectra of a Jet in PKS 0637-752’, ApJ, in press. Chiang, J. and Dermer, C. D. (1999), ‘Synchrotron and Synchrotron Self-Compton Emission and the Blast-Wave Model of Gamma-Ray Bursts’, ApJ, 512, 699. Christiansen, W. (1969), ‘The Dynamics and Structure of Inertially Confined Clouds’, MNRAS, 145, 327. Clarke, D. A., Harris, D. E., and Carilli, C. L. (1997), ‘Formation of Cavities in the X-ray Emitting Cluster Gas of Cygnus A’, MNRAS, 284, 981. Coleman, C. S. and Bicknell, G. V. (1988), ‘Jets with Entrained Clouds. II - Synchrotron Spectrum and Emission Structure’, MNRAS, 230, 497. Curtis, H. D. (1918), ‘Descriptions of 762 Nebulae and Clusters, Photographed with the Crossley Reflector’, Lick Obs. Pub., 13, 11. Dai, Z. G. and Lu, T. (1998), ‘Gamma-ray Burst Afterglows: Effects of Radiative Corrections and Non-Uniformity of the Surrounding Medium’, MNRAS, 298, 87. De Kool, M., Begelman, M. C., and Sikora, M. (1989), ‘Self-Absorbed Synchrotron Sources in Active Galactic Nuclei’, ApJ, 337, 66. Dermer, C. D. and Mitman, K. E. (1999), ‘Short-Timescale Variability in the External Shock Model of Gamma-Ray Bursts’, ApJ, 513, L5. Drury, L. O., Axford, W. I., and Summers, D. (1982), ‘Particle Acceleration in Modified Shocks’, MNRAS, 198, 833. Eichler, D. (1993), ‘Magnetic Confinement of Jets’, ApJ, 419, 111. Elvis, M., Wilkes, B. J., McDowell, J. C., Green, R. F., Bechtold, J., Willner, S. P., Oey, M. S., Polomski, E., and Cutri, R. (1994), ‘Atlas of Quasar Energy Distributions’, ApJS, 95, 1. Fabian, A. C. (1994), ‘Cooling Flows in Clusters of Galaxies’, ARA&A, 32, 227. Fabian, A. C., Nandra, K., Reynolds, C. S., Brandt, W. N., Otani, C., Tanaka, Y., Inoue, H., and Iwasawa, K. (1995), ‘On broad Iron K-alpha Lines in Seyfert 1 Galaxies’, MNRAS, 277, L11. 162 Fanaroff, B. L. and Riley, J. M. (1974), ‘The Morphology of Extragalactic Radio Sources of High and Low Luminosity’, MNRAS, 167, 31. Fanti, R., Fanti, C., Dallacasa, D., Schlizzi, R. T., Spencer, R. E., and Stanghellini, C. (1995), ‘Are Compact Steep-Spectrum Sources Young?’, A&A, 302, 317. Fanti, R., Fanti, C., Schlizzi, R. T., Spencer, R. E., Rendong, Nan, Parma, P., Breugel, W. J. M.van, and Venturi, T. (1990), ‘On the Nature of Compact Steep Spectrum Radio Sources’, A&A, 231, 333. Fenimore, E. E. et al. (1999a), ‘Gamma-Ray Bursts and Relativistic Shells: The Surface Filling Factor’, ApJ, 512, 683. Fenimore, E. E., Madras, C. D., and Nayakshin, S. (1996), ‘Expanding Relativistic Shells and Gamma-Ray Burst Temporal Structure’, ApJ, 473, 998. Fenimore, E. E., Ramirez-Ruiz, E., and Wu, B. (1999b), ‘GRB 990123: Evidence that the Gamma Rays Come from a Central Engine’, ApJ, 518, L73. Ford, H. C. et al. (1994), ‘HST FOS Spectroscopy of M87: Evidence for a Disk of Ionized Gas Around a Massive Black Hole’, ApJ, 435, L27. Frank, J., King, A., and Raine, D. (1990), Accretion Power in Astrophysics, volume 20 of Cambridge Astrophysics Series, Cambridge, Cambridge University Press, 2 edition. Goldreich, P. and Sridhar, S. (1995), ‘Toward a Theory of Interstellar Turbulence. II. Strong Alfvenic Turbulence’, ApJ, 438, 763. Goldreich, P. and Sridhar, S. (1997), ‘Magnetohydrodynamic Turbulence Revisited’, ApJ, 485, 680. Harrison, F. A. et al. (1999), ‘Optical and Radio Observations of the Afterglow from GRB 990510: Evidence for a Jet’, ApJ, 523, L121. Heinz, S. (1997), ‘Analysis of the Synchrotron Emission from the M87 Jet’, Master’s thesis, University of Colorado, Boulder. Heinz, S. and Begelman, M. C. (1997), ‘Analysis of the Synchrotron Emission from the M87 Jet’, ApJ, 490, 653. Heinz, S. and Begelman, M. C. (1999), ‘A Shotgun Model for Gamma-Ray Busts’, ApJ, 527, L35. Heinz, S. and Begelman, M. C. (2000), ‘Jet Acceleration by Tangled Magnetic Fields’, ApJ, 535, 104. Heinz, S., Reynolds, C. S., and Begelman, M. C. (1998), ‘X-Ray Signatures of Evolving Radio Galaxies’, ApJ, 501, 126. Heyvaerts, J. and Norman, C. (1989), ‘The Collimation of Magnetized Winds’, ApJ, 347, 1055. Hughes, P. A. and Miller, L. (1995), ‘Synchrotron and Inverse-Compton Radiation’, in Beams and Jets, Hughes, P. A. (ed), volume 19 of Cambridge Astrophysics Series, page 1, Cambridge: Cambridge University Press. 163 Junor, W. and Biretta, J. A. (1995), ‘The Radio Jet in 3C274 at 0.01 PC Resolution’, AJ, 109, 500. Kaiser, C. R. and Alexander, P. (1999), ‘Heating of the Intergalactic Medium by FR II Radio Sources’, MNRAS, 305, 707. Kartje, J. F., Königl, A., and Elitzur, M. (1999), ‘Megamaser Disks in Active Galactic Nuclei’, ApJ, 513, 180. Katz, J. I. (1994a), ‘Low-Frequency Spectra of Gamma-Ray Bursts’, ApJ, 432, L27. Katz, J. I. (1994b), ‘Two Populations and Models of Gamma-Ray Bursts’, ApJ, 422, 248. Katz, J. I. (1997), ‘Yet Another Model of Gamma-Ray Bursts’, ApJ, 490, 633. Kirk, J. G. (1994), Plasma Astrophysics, Benz, A. O. and Courvoisier, T. J. L. (eds.), volume 24 of Saas-Fee Advanced Course, page 225, Berlin: Springer. Kirk, J. G. and Heavens, A. F. (1989), ‘Particle Acceleration at Oblique Shock Fronts’, MNRAS, 239, 995. Krolik, J. H. (1999), ‘Magnetized Accretion Inside the Marginally Stable Orbit Around a Black Hole’, ApJ, 515, L73. Kumar, P. (1999), ‘Gamma-Ray Burst Energetics’, ApJ, 523, L113. Laing, R. A (1980), ‘A Model for the Magnetic-Field Structure in Extended Radio Sources’, MNRAS, 193, 439. Li, Z. Y., Chiueh, T., and Begelman, M. C. (1992), ‘Electromagnetically Driven Relativistic Jets - A Class of Self-Similar Solutions’, ApJ, 394, 459. Livio, M., Ogilvie, G. I., and Pringle, J. E. (1999), ‘Extracting Energy from Black Holes: The Relative Importance of the Blandford-Znajek Mechanism’, ApJ, 512, 100. Lubow, S. H., Papaloizou, J. C. B., and Pringle, J. E. (1994a), ‘Magnetic Field Dragging in Accretion Disks’, MNRAS, 267, 235. Lubow, S. H., Papaloizou, J. C. B., and Pringle, J. E. (1994b), ‘On the Stability of Magnetic Wind-Driven Accretion Disks’, MNRAS, 268, 1010. Luo, Q. and Protheroe, R. J. (1999), ‘Radiation Force on Relativistic Jets in Active Galactic Nuclei’, MNRAS, 304, 800. Macchetto, F., Marconi, A., Axon, D. J., Capetti, A., Sparks, W., and Crane, P. (1997), ‘The Supermassive Black Hole of M87 and the Kinematics of Its Associated Gaseous Disk’, ApJ, 489, 579. Meszaros, P. and Rees, M. J. (1997), ‘Poynting Jets from Black Holes and Cosmological Gamma-Ray Bursts’, ApJ, 482, L29. Mathews, W. G. and Blumenthal, G. R. (1977), ‘Rayleigh-Taylor Stability of Compressible and Incompressible Radiation-Supported Surfaces and Slabs: Application to QSO Clouds’, ApJ, 214, 10. 164 McNamara, B.R̃., Wise, M., Nulsen, P. E.J̃., David, L.P̃., Sarazin, C.L̃., Bautz, M., Markevitch, M., Vikhlinin, A., Forman, W.R̃., Jones, C., and Harris, D.Ẽ. (2000), ‘Chandra X-Ray Observations of the Hydra A Cluster: An Interaction between the Radio Source and the XRay-emitting Gas’, ApJ, 534, L135. Meisenheimer, K. (1992), ‘The Spectra of Extended Radio Jets and Hot Spots’, in Physics of Active Galactic Nuclei, Duschl, W. J. and Wagner, S. J. (eds.), page 525, Berlin: Springer. Meisenheimer, K. (1999), ‘High-Frequency Observations and Spectrum of the Jet in M87’, in The Radio Galaxy Messier 87, Röser, H. J. and Meisenheimer, K. (eds.), volume 530 of Lecture Notes in Physics, page 188, Berlin: Springer. M99. Meisenheimer, K., Röser, H. J., Hiltner, P.R., Yates, M.G., Longair, M.S., Chini, R., and Perley, R.A. (1989), ‘The Synchrotron Spectra of Radio Hot Spots’, A&A, 219, 63. Meisenheimer, K., Röser, H. J., and Schlötelburg, M. (1996), ‘The Synchrotron Spectrum of the Jet in M87’, A&A, 307, 61. ski, B., and Piran, T. (1992), ‘Gamma-Ray Bursts as the Death Throes of Narayan, R., Paczyn Massive Binary Stars’, ApJ, 395, L83. Narayan, R. and Yi, I. (1994), ‘Advection-Dominated Accretion: A Self-Similar Solution’, ApJ, 428, L13. Neumann, M., Meisenheimer, K., Röser, H. J., and Fink, H. H. (1996), ‘ROSAT-HRI Observations of the Jet in M 87.’, A&A, 318, 383. Nielsen, E. H., Tsvetanov, Z. I., and Ford, H. C. (1999), ‘The Surface Brightness Fluctuations and Globular Cluster Populations of M87 and its Companions’, in The Radio Galaxy Messier 87, Röser, H. J. and Meisenheimer, K. (eds.), volume 530 of Lecture Notes in Physics, page 50, Berlin: Springer. O’Dea, C. P., Baum, S. A., and Stanghellini, C. (1991), ‘What are the Gigahertz PeakedSpectrum Radio Sources?’, ApJ, 380, 66. O’Dell, S. L. (1981), ‘Radiation Force on a Relativistic Plasma and the Eddington Limit’, ApJ, 243, L147. Okamoto, I. (1979), ‘Relativistic Centrifugal Winds’, MNRAS, 185, 69. Owen, F. N., Hardee, P. E., and Cornwell, T. J. (1989), ‘High-Resolution, High Dynamic Range VLA Images of the M87 Jet at 2 Centimeters’, ApJ, 340, 698. ski, B. (1998), ‘Are Gamma-Ray Bursts in Star-Forming Regions?’, ApJ, 494, L45. Paczyn Panaitescu, A., Spada, M., and Meszaros, P. (1999), ‘Power Density Spectra of Gamma-Ray Bursts in the Internal Shock Model’, ApJ, 522, L105. Parker, E. N. (1958), ‘Dynamics of the Interplanetary Gas and Magnetic Fields.’, ApJ, 128, 664. Pedlar, A., Ghataure, R. D., Davies, R. D., Harrison, B. A., Perley, R., Crane, P. C., and Unger, S. W. (1990), ‘The Radio Structure of NGC1275’, MNRAS, 246, 447. 165 Perley, R. A., Bridle, A. H., and Willis, A. G. (1984), ‘High-Resolution VLA Observations of the Radio Jet in NGC 6251”’, ApJS, 54, 291. Perola, G. C. and Tarenghi, M. (1980), ‘IUE Spectra of the Jet and the Nucleus of M87’, ApJ, 240, 2. Phinney, E. S. (1982), ‘Acceleration of a Relativistic Plasma by Radiation Pressure’, MNRAS, 198, 1109. Phinney, E. S. (1983), ‘A Theory of Radio Sources’, PhD thesis, University of Cambridge, Cambridge. Piran, T. (1999), ‘Gamma-Ray Bursts and the Fireball Model’, Phys. Rep., 314, 575. Readhead, A. C. S., Taylor, G. B., and Pearson, T. J. (1996), ‘Compact Symmetric Objects and the Evolution of Powerful Extragalactic Radio Sources’, ApJ, 460, 634. Rees, M. J. (1966), ‘Appearance of Relativistically Expanding Radio Sources’, Nature, 211, 468. Rees, M. J. (1978a), ‘Accretion and the Quasar Phenomenon’, Phys. Scr, 17, 193. Rees, M. J. (1978b), ‘The M87 jet - Internal Shocks in a Plasma Beam’, MNRAS, 184, 61. Rees, M. J. and Meszaros, P. (1994), ‘Unsteady Outflow Models for Cosmological Gamma-Ray Bursts’, ApJ, 430, L93. Rees, M. J. and Meszaros, P. (1992), ‘Relativistic Fireballs - Energy Conversion and TimeScales’, MNRAS, 258, 41. Renaud, N. and Henri, G. (1998), ‘The Terminal Bulk Lorentz Factor of Relativistic ElectronPositron Jets’, MNRAS, 300, 1047. Reynolds, C. S. and Begelman, M. C. (1997), ‘Intermittent Radio Galaxies and Source Statistics’, ApJ, 487, L135. Reynolds, C. S., Di Matteo, T., Fabian, A. C., Hwang, U., and Canizares, C. R. (1996a), ‘The ‘Quiescent’ Black Hole in M87’, MNRAS, 283, L111. Reynolds, C. S., Fabian, A. C., Celotti, A., and Rees, M. J. (1996b), ‘The Matter Content of the Jet in M87: Evidence for an Electron-Positron Jet’, MNRAS, 283, 873. Rhoads, J. E. (1997), ‘How to Tell a Jet from a Balloon: A Proposed Test for Beaming in Gamma-Ray Bursts’, ApJ, 487, L1. Rybicki, G. B. and Lightman, A. P. (1979), Radiative Processes in Astrophysics, New York, Wiley. Sandage, A. (1961), The Hubble Atlas of Galaxies, Washington, Carnegie Institution of Washington. Sari, R. and Piran, T. (1995), ‘Hydrodynamic Timescales and Temporal Structure of GammaRay Bursts’, ApJ, 455, L143. 166 Sari, R. and Piran, T. (1997), ‘Variability in Gamma-Ray Bursts: A Clue’, ApJ, 485, 270. Sari, R., Piran, T., and Halpern, J. P. (1999), ‘Jets in Gamma-Ray Bursts’, ApJ, 519, L17. Scheuer, P. A. G. (1974), ‘Models of Extragalactic Radio Sources with a Continuous Energy Supply from a Central Object’, MNRAS, 166, 513. Scheuer, P. A. G. (1982), ‘Morphology and Power of Radio Sources, ’, in IAU Symp. 97: Extragalactic Radio Sources, volume 97, page 163. Shaviv, N. J. and Dar, A. (1995), ‘Fireballs in Dense Stellar Regions as an Explanation of Gamma-Ray Bursts’, MNRAS, 277, 287. Sikora, M., Sol, H., Begelman, M. C., and Madejski, G. M. (1996), ‘Radiation Drag in Relativistic Active Galactic Nucleus Jets’, MNRAS, 280, 781. Sparks, W., Biretta, J. A., and Macchetto, F. (1996), ‘The Jet of M87 at Tenth-Arcsecond Resolution: Optical, Ultraviolet, and Radio Observations’, ApJ, 473, 254, SBM. Sridhar, S. and Goldreich, P. (1990), ‘Toward a Theory of Interstellar Turbulence. I. Weak Alfvenic Turbulence’, ApJ, 432, 612. Stanek, K. Z., Garnavich, P. M., Kaluzny, J., Pych, W., and Thompson, I. (1999), ‘BVRI Observations of the Optical Afterglow of GRB 990510’, ApJ, 522, L39. Stiavelli, M., Peletier, R., and Carollo, C. M. (1997), ‘M87 in the Near-Infrared: the Jet and the Counterjet Regions’, MNRAS, 285, 181. Stocke, J. T., Rieke, G. H., and Lebofsky, M. J. (1981), ‘New Observational Constraints on the M87 Jet’, Nature, 294, 319. Thompson, C. (1994), ‘A Model of Gamma-Ray Bursts’, MNRAS, 270, 480. Tout, C. A. and Pringle, J. E. (1996), ‘Can a Disk Dynamo Generate Large-Scale Magnetic Fields?’, MNRAS, 281, 219. White, D. A., Jones, C., and Forman, W. (1997), ‘An Investigation of Cooling Flows and General Cluster Properties from an X-Ray Image Deprojection Analysis of 207 Clusters of Galaxies’, MNRAS, 292, 419. White, R. E. and Sarazin, C. L. (1988), ‘Star Formation in the Cooling Flows of M87/Virgo and NGC 1275/Perseus’, ApJ, 335, 688. Wilkinson, P. N., Polatidis, A. G., Readhead, A. C. S., Xu, W., and Pearson, T. J. (1994), ‘TwoSided Ejection in Powerful Radio Sources: The Compact Symmetric Objects’, ApJ, 432, L87. Woods, E. and Loeb, A. (1995), ‘Empirical Constraints on Source Properties and Host Galaxies of Cosmological Gamma-Ray Bursts’, ApJ, 453, 583. Woosley, S. E. (1993), ‘Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes’, ApJ, 405, 273. 167 Young, P. J., Westphal, J. A., Kristian, J., Wilson, C. P., and Landauer, F. P. (1978), ‘Evidence for a Supermassive Object in the Nucleus of the Galaxy M87 from SIT and CCD Area Photometry’, ApJ, 221, 721. Appendix A A More Realistic Dissipation Law for the Tangled Field Model The dissipation law we assumed in x2.2.1.2 was only one of many plausible ad hoc models. Since (for finite conductivity, i.e., beyond the limit of perfect MHD) reconnection will occur whenever there is field reversal on sufficiently small scales (which would certainly be the case in a highly tangled geometry), we would expect dissipation to occur even if there were no change in field geometry due to expansion or acceleration. In that case we might expect that the dissipation timescale is proportional to the time it takes a disturbance to travel a given characteristic length (e.g., the jet width) in the comoving frame, i.e., dU 0 i v U 0 i Alfven ; dz diss R (A.1) absorbs the effects of resistivity and all the unknown physics of the where the parameter reconnection process. Once again, it is straightforward to generalize to the case of different i for different components of the field. It is possible to solve the set of equations in the magnetically dominated case (i.e., setting 0 + 4p0 = 0), under the assumption that = const: and in the relativistic limit, limit vAlfven = 1, which simplifies the treatment significantly. 1. In this We assume that the dissipated energy is radiated away immediately, which leads to a modified equation (2.15) 2 + 6 d + (2 + 2 ) R 3 3 dz (2 + 2 ) dR = 0: Rdz (A.2) The pressure balance equation (2.17) is also modified: ( 1) d dz (3 + ) dR Rdz = =z R (A.3) 169 where we used U 0 (z ) = / pext and equation (2.20). This set of equations can be solved to give n h =4 1 A (z=z )1 0 (z=z0 ) 0 =2 1 io(3+5 )=(4+4 ) ; (A.4) with A 1 : R (1 = 2)(1 + 3 ) 0 0 (A.5) 0 denote quantities evaluated at some arbitrary upstream point z0 . In the limit of ! 0 this solution appropriately reduces to the result without dissipation, i.e., / z=4. The Subscripts solution can essentially take on three different behaviors: If > 2, the solution will asymptot- / z=4, i.e., = 1=4. If < 2, on the other hand, two different scenarios 6 1=4 (but still constant) can occur: the flow can either approach a self-similar behavior with = in the limit of z z0 , or, if A > 0 (i.e., > 1=3), the flow can actually stall, i.e., ! 0 for z ! z0 [(1 =2) (1 + 3 ) =A 1]1=(1 =2) . In this limit, the magnetic field dissipates ically approach away too quickly to satisfy pressure balance and the jet must contract and decelerate to increase its internal pressure, thereby increasing its dissipation rate, which leads to a run-away process. Eventually, the massless approximation will break down, in which case the Alfven velocity will drop, lowering the dissipation rate (furthermore, the particle pressure will gain in importance, eventually stabilizing the jet against external pressure, in which case the jet would behave as described by BR74). This process would produce an observable hot-spot (and possibly a shock) at a fixed distance. Appendix B Details of Synchrotron Emission B.1 Synchrotron radiation In this appendix, we will give a brief overview of the properties of synchrotron radiation that are important in this paper. We will mainly follow the review by Rybicki and Lightman (1979). B.1.1 Synchrotron Losses: Synchrotron radiation is produced by relativistic particles moving in a magnetic field, thus it is the relativistic equivalent to cyclotron radiation, the crucial distinction being time dilation and Doppler beaming effects. Consider a charged particle moving trough a homogeneous magnetic field B with velocity v c. The Lorentz force perpendicular to the magnetic field will cause it to perform circular motion around the field line with frequency !B where qB=(mc), q is the particle charge, its Lorentz factor, m its mass, and c the speed of light. This circular motion is superposed on the linear motion of the particle along the field, thus it will travel on a helical trajectory. In its rest frame the particle will experience an acceleration v velocity . The magnitude of this acceleration is given by a = a? perpendicular to its a? = !B v?. Using the Larmor formula for the power an accelerated particle emits (which is covariant if the radiation process 171 is forward-backward symmetric), we arrive at a loss of dW = dt 2q2 jaj2 2q 4 2 B 2 2 = v : 3c3 3c5 m2 ? Averaging over an isotropic distribution of pitch angles we arrive at an average loss rate per particle of d = dt 4q4 B 2 2 ; 9c5 m3 or, expressed for the particle momentum: dp 4q 4 B 2 p2 = = Ap2 ; dt 9c6 m4 (B.1) where A from chapter 3.2 and vparticle c have been used. From this we can easily derive the synchrotron loss time of a particle with an initial momentum p0 , which we define as the time it takes the particle to lose half of its energy due to synchrotron losses in a constant magnetic field: tloss (p0 A) B.1.2 1 (B.2) Emitted Synchrotron Spectrum: To derive the expression for the spectral emissivity we need to recall the expression for the energy in the electric field of an accelerated particle moving at velocity Z dW 2 2 2 2 = (q ! =4 c ) d!d n (n v) exp i!(t0 v(t) 2 n r0(t0 )=c)dt0 ; (B.3) n is the line of sight normal at an angle # to v0 , the particles velocity at retarded time t0 = 0, and r0 (t0 ) the particles retarded position. Using the small angle approximation for sin and cos to leading order, v c, and (1 v=c) (2 2 ) 1 , the factor (t0 n r (t0 )=c) can where approximately be written as t0 cos # sin !B sin (t0 ) !B sin (2 2 ) 1 " (sin ) (1 + 2 #2 )t0 + !B2 2 3 2 t03 # : 172 Accordingly, we can write n (n v)=c = ek cos (!B sin t0 )sin# e? sin (!B sin t0) ek # e?!B sin t0 The small angle approximation is valid here because the integrand in equation (B.3) becomes highly oscillatory for large arguments, thus the integral itself goes to zero. The integral in equation (B.3) can be expressed in terms of the modified Bessel function K 53 . We can define the critical frequency, the frequency at which the emissivity for a particle with given energy mc2 peaks, to be (see equation [3.8]): 2 sin # 3 qB 2mc !crit ( ) and, after averaging over solid angle, arrive at the formula for the power radiated per particle: p 3q3 B sin # ! Z 1 K 5 (y)dy P (!) = 2mc2 !crit !=!crit 3 (B.4) For a power law momentum distribution as defined in equation (3.1), equation (B.4) yields a spectral emissivity of j (!) = N0 (mc)(a 5)=2 C1 N0 (B sin #)(a B.1.3 p 3q3 B sin # 2c(a 1) 3a + 13 12 1)=2 ! ( a+3)=2 3a 7 12 ! 3qB sin # (a 3)=2 (B.5) Equipartition: With equation (B.5) and the assumption of equipartition between energy density in rela- tivistic particles Uparticle and magnetic field energy density netic field Beq . B 2 =8 we can solve for the mag- Its value depends on the spectral slope and the cutoff in the momentum dis- tribution at low (pmin ) and high energies (pmax ), since we have to integrate the momentum distribution from equation (3.1) to find the total energy density Uparticle = Z pmax pmin N0 cp3 a dp = 8 h > > < N0 c p4 a 4 a > > : max N0 c log ppmax min N0 C 2 p4mina i (for a 6= 4) (for a = 4) 9 > > = 173 > > ; Setting this equal to the magnetic field energy density we can solve for N0 in terms of Beq and insert this into equation (B.5), which enables us to solve for Beq : ! 3)=2 2=(a+3) 8C2 jobserved !(a Beq = C1 B.2 1 a sin #( a+3 ) (B.6) The Transport Equation Equation (3.4), the transport equation, is of Fokker-Planck type, where the left hand side represents the total advective derivative in phase space and the right hand side corresponds to a scattering term due to radiative losses. Following Coleman and Bicknell (1988) we can introduce a new variable q p% 1=3 and rewrite equation (3.4) as df p d% @f df + = + dt 3% dt @p dt Df = Dt dp Dq p @f dt Dt q @p Dq @f Dt @q @ 4 = Aq 2 %1=3 qf : @q Here, f = f (t; x; p) is the momentum distribution function for assumed anisotropy. We define D Dt @ @t@ + v r + dp dt @p to be the total advective time derivative in phase space. It follows that D4 Dq q f 4q3 f Dt Dt q4 Dq @f D 4 Dq @ 4 = qf qf Dt @q Dt Dt @q @ 4 = Aq2 %1=3 qf @q or, in the fluid rest frame @4 @ 4 Dq qf = qf + Aq2 %1=3 : @t @q Dt 174 Using the method of characteristics, we can solve this equation by finding the streamlines in q t space, along which the quantity q4 f is conserved, i.e., we solve the characteristic equation Dq = Dt Aq2 %1=3 ; which yields q = q(t0 ) R 1 + q(t0 ) tt0 A%1=3 dt0 q(t0 ) 1 + q(t0 )(%0 )1=3 with the obvious definition for . This leads directly to equation (3.5). From the fact that q 4 f is conserved along characteristics, we can easily see that the expected spectral shape of a cooled power law is given by f (p) = f (p0 ) B.3 % 4=3 p0 4 =p %0 p a % 4=3 (1 p )a %0 4 (B.7) Spectral Cutoff Shapes M99 used the 2 cm VLA maps by Owen et al. (1989) and ground based high resolution data in the B, R, I, H, and K bands to fit a model spectrum along the jet. They assumed a power law with sharp cutoff in the electron momentum distribution that drops immediately to zero at the cutoff momentum and they left the power law index and the cutoff momentum as free parameters. However, in Appendix B.2 we showed that the cutoff that naturally develops due to synchrotron losses upstream tends to have a different spectral shape around the cutoff, depending on the power law index a of the injected particle distribution. For a 4:3, i.e., for RO 0:65, the expected cutoff in the synchrotron spectrum will be less sharp. Both cases are shown in Figure B.1. As diffusion processes will also wash out the sharpness of the cutoff, we should theoretically expect the spectrum to fall off less steeply than what was assumed in the fit. This demonstrates that the error estimate by M99 is rather optimistic, as it does not take uncertainties in the exact shape of the cutoff into account (which could potentially have an 175 100 cutoff momentum pc f(p) [arbitrary units] 102 10-2 10-4 10-6 10-8 10 101 100 j(ν) [arbitrary units] 1000 cutoff frequency νc 100 momentum p [arbitrary units] 10-1 10-2 10-3 sharp cutoff natural cutoff 10-4 10-5 102 103 104 105 ν [arbitrary units] 106 107 Figure B.1: Electron momentum distributions and corresponding synchrotron spectra calculated for two different cutoff shapes. solid line: steep cutoff; dashed line: cutoff according to synchrotron cooled distribution. All units are arbitrary. effect on the amplitude of variations seen in the best fit c ). With increased error bars, our model would yield more acceptable values for 2min , especially in the post knot A region. Appendix C Derivation of the Dispersion Relation for the Relativistic Rayleigh-Taylor Instability The derivation of the Rayleigh Taylor instability for a relativistic plasma by Allen and Hughes (1984) is based on the formalism used in Chandrasekhar (1961), using Eulerian rather than Lagrangian first order variables, which is not a particularly transparent derivation and is formally not self-consistent (thought is does produce the correct results). Since the dispersion relation given by Allen and Hughes (1984) contains typographical errors we found it appropriate to derive the fully relativistic dispersion relation for any ideal gas (i.e., for arbitrary adiabatic indices ad and arbitrary ratios of random internal energy to rest mass energy density). It should also be noted that the incompressible analysis commonly used is only valid for wavelengths smaller compared to the scale height in the fluid, even in the non-relativistic case. The analysis by Mathews and Blumenthal (1977) assumes isothermal perturbations, which is not a realistic assumption in the cases we are interested in. The equation of motion is given by T i ; ui T 0 ; = 0, where we assumed the Einstein summation convention, i runs from 1 to 3. u is the four-velocity, Here, w the stress-energy the fluid Lorentz factor. After a little algebra, this can be written as tensor, and 2w T @v @p 2 + (v r) v v=c + rp = 0: @t @t (C.1) = e + p is the enthalpy, e is the internal energy, p is the pressure, and the rest mass density, all measured in the fluid rest frame. For polytropic gases, e = 1=(ad is the ratio of specific heats; v is the three-velocity, vi = ui= , i from 1 to 3. 1)p where ad 177 The continuity equation for a conserved particle number density n can be written as @ @ +r n+n + r( v) = 0; @t @t (C.2) while the equation of state is @ @ + r p + p + r( v) = 0: @t @t (C.3) All of these equations are fully general within the limits of special relativity (i.e., weak gravity). Specializing to Rayleigh-Taylor instability, we assume that a gravitational field is present equivalent to the acceleration of the plasma in the GRB. We will assume that a planar contact discontinuity exists in the fluid, placed at z = 0. Gravity is assumed to act perpendicularly to that surface. The background flow is compressible, so for self-consistency we must assume that the density and pressure of the background flow are stratified. For mathematical simplicity we will assume that the gas has an exponential dependence and is isothermal on either side of the discontinuity. Without loss of generality, we can also specify that the x-axis lie along the k direction of the wave vector . Assuming small perturbations in the dynamical quantities, we can linearize the equations. We can then Fourier transform the linearized equations in x and t and transform to a coordinate system in which the perturbed interface is at rest. The new coordinates are (Mathews and Blumenthal 1977): n x i t k z = z 0 exp (ikx + nt); (C.4) where is the (first order) displacement of the interface. The perturbed equations then take the form @w @ ) + (w n ) = 0 @ @ @p @w np~ + ad p(ikv + ) + (w n ) = 0 @ @ @p nhv + ikp~ ik = 0 @ @ p~ nhw + + gh~ = 0 @ n~ + (ikv + (C.5) 178 Here, a ~ indicates a first order quantity, v and w are the (first order) velocity in the x and z directions, and n i! , where ! is the temporal frequency. The equations also indicate that the dependence of all first order quantities is the same. Furthermore, the zeroth order quantities also have the same dependence (by assumption). A little algebra then gives @2w @ 2 g " h p 1 1 @w c2 @ !# hn2 1 k2 g2 2 + +k w=0 ad n2 p pad (C.6) This equation has the well known solution w = C+ exp K+ + C exp K (C.7) where C+ and C are constants to be determined later and K = hg 2p g 2c2 s g 2 hg + 1 2p 2c2 (C.8) 1 k2 g2 hn2 + + k2 2 ad n p pad Since the energy contained in the perturbation must be finite, we must chose the constants C such that the solution decays exponentially away from the interface. In other words, the real part of K must be negative (positive) for positive (negative) . The equations of motion dictate that the pressure be continuous across the discontinuity. Equating the first order pressure on both sides finally leads to the dispersion relation. A little algebra reveals p~ = k2 p + n2 nw @p h ad @ 2 pk ad 2 n + h ad np @w @ : (C.9) The dynamic boundary condition is simply 1 w = (w vk ) = ; n n (C.10) 179 dropping the second order term. This is derived from requiring that the fluid on both sides of the interface move parallel to each other, in other words, no fluid crosses the interface. Together, these equations yield k2 gh1 + n2 K1 h1 k2 gh2 + n2 K2 h2 = n2 h2 : n2 h1 + k 2 2 ad;1 p1 p2 + k ad;2 Here the subscripts 1 and 2 denominate the two sides of the shock. (C.11)