Download millmans theorem

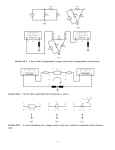
Kirchhoff Laws against Node-Voltage Analysis and Millman's Theorem
Marcela Niculae1 and C. M. Niculae2
1
Ion Barbu theoretical high school, Bucharest
2
University of Bucharest, Faculty of physics, Atomistilor 405, Bucharest-Magurele, CP MG-11, 077125, RO
E-mail: [email protected]
The present paper aims at introducing a new method for teaching electric circuits in high schools. Using
the Kirchhoff's laws to solve electric networks of medium complexity involves a great deal of less
appealing mathematical effort. Instead, we propose a more efficient algorithm that combines the nodevoltage analysis with Millman's theorem. The method is simple enough, and requires less effort to solve
electric circuits of medium complexity. It is this simplicity that improves the student ability to correctly
solve the problem.
Circuit analysis normally refers to finding all node voltages and all branch currents for an
electrical circuit. In this paper we call this task solving the fundamental problem of the circuit,
or, in short, solving the circuit.
Several methods are available for linear circuit analysis [1]. The most important are: Branch
current method and Mesh current method. Apart from these there are other methods such as:
Superposition, Source transformations, and Equivalent circuits. These methods combine one of
the main methods with powerful theorems such as: Millman's Theorem [2, 3], Superposition
Theorem, Thévenin's Theorem and Norton's Theorem (see [4,5] for an historical review about
the Equivalent Circuit Concept). Of course, all of these efficient methods are based on Ohm's
and Kirchhoff's Laws.
The curricula of Romanian high school dedicated to circuit analysis recommends a direct method
based on Kirchhoff's laws to be used in applications. Teaching experience showed that this
method is time consuming, and less motivating for students. On the other hand, at the academic
level, any basic course on electric circuits introduces proper theorems and methods for such an
analysis. The experience of teaching, based on a statistical evaluation of students, showed that
when students make use of these theorems and methods they respond faster, providing right
answers and solutions.
The elements of an electrical network are: the nodes, the branches, and the loops. Their
definitions are well known (see for example [1]).
•
•
•
•
•
•
•
branch is a part of a circuit that contains at least a resistor or a voltage source and connect
two nodes.
node is the junction of two or more branches.
loop is any closed connection of branches.
reference node (or reference), is a node in the circuit, with respect to which all other
voltages are measured.
node voltage is measured with respect to reference node.
Kirchhoff Current Law (also known as Kirchhoff's first law) (KCL). The sum of all
currents flowing into a node is zero.
Kirchhoff Voltage Law (Kirchhoff's second law) (KVL). The sum of all voltages around a
loop is zero.
In electrical engineering, the branch current method (BCM), also known as nodal analysis or
node-voltage analysis, is used to determine the voltage (potential difference) between nodes in
an electrical circuit. Here, we present a brief description of this method that solves the system of
KCL and KVL equations in terms of node voltages.
The steps of BCM method are:
•
•
•
Assume directions of currents in each branch, as is presently done in the method based
on Kirchhoff's laws.
Chose one of the circuit nods as reference. When choosing the reference node, select
the node with the most connections .
Write KCL equations.
(1)
∑ Ii − ∑ Io = 0
where I i and I 0 are currents that flow into, leave (flow out) the node, respectively.
• Write the Generalized Ohm's Law (GOL) equation for each branch of the circuit.
VA − VB = ∑ E p − ∑ En − I k ∑ Rm
(2)
where I k is the branch current,
∑R
m
is the branch equivalent resistance,
∑E −∑E
p
n
is the
equivalent voltage source of the branch, VA and, VB are the voltages at the ends of the k branch.
• Solve each one of the above equations for the branch current as
I k = (− VA + VB + ∑ E p − ∑ En ) / ∑ Rm .
(3)
•
•
•
Substitute these currents in KCL system (1).
Solve this system for node voltages.
Substitute these voltages in equations (3) and calculate the branch currents.
This method is particularly efficient since for most circuits encountered in practice, the number
of independent nodes is smaller than the number b of branches.
Millman's Theorem, also known as parallel generator theorem, allows for the calculation of a
node voltage, in terms of voltages at neighboring nodes [2, 3]. Let X be a node having N
neighbors (see figure 1).
Fig. 1. Circuit with a common node X connected to N branches.
The Millman's Theorem states that the voltage of the node X is given by
 V  
1 
VX =  ∑ k  /  ∑ 
(4)
 Rk   Rk 
That is, the voltage at X is the sum of branch voltages, multiplied by their associated
admittances, divided by the total admittance. By total admittance we mean the inverse of the
equivalent resistance of the N resistors connected in parallel. At the high school level, the
admittance, Y, is defined as the inverse of electrical resistance, 1 / R .
The steps of our method are:
•
•
•
•
•
•
Simplify, if possible, the circuit branches. For instance, if a branch has more than one
source voltage, merge them into a single one. Do the same for branch resistances (see
definitions associated with system 2).
Chose one of the nodes in the circuit as reference node. See step 2 of BCM method.
Apply Millman's theorem to each independent node of the circuit.
Solve the above system in terms of node voltages.
Assume directions of currents in each branch.
Write Ohm's law for each branch and solve it for branch current.
The simplification mentioned as a first step is possible because it is always possible to find an
equivalent branch which has a single voltage source in series with a resistor. In fact, this is the
main result of the Thévenin's theorem [1, 4].
At high school level, Thévenin's theorem for linear electrical networks can be stated as follows:
Any combination of voltage sources and resistors with two terminals is electrically equivalent to
a single voltage source V, and a single series resistor R.
Consider the circuit shown in figure 2.
0.99kΩ
4V
1kΩ
2kΩ
10V
1.99kΩ
4kΩ
10Ω
10Ω
Fig. 2. The test problem.
Problem: Solve this circuit (i.e. find node voltages and branch currents).
For the purpose of comparison, this problem will be solved using: Kirchhoff's laws method, the
branch current method, and our method.
The test circuit has 5 branches (see figure 3)
I1
E1
R1
A I5
R5
I
r1
R2
I2
I4
I3
R3
B
II
R4
C
III
E2
r2
Fig. 3. For each branch of the test circuit we assumed a direction for the current. We consider three loops
and assumed a direction for each one.
Notice that this circuit has 6 loops and 7 nodes, but only 3 loops and 2 nodes are independent.
When A and B are chosen as independent nodes, Kirchhoff's current laws for these nodes may be
written as
I1 = I 3 + I 5 ,
I 4 = I 2 + I5.
( A)
(B )
Kirchhoff's voltage law applied to loops I, II, and III gives
(5)
E1 = (r1 + R1 ) ⋅ I1 + R3 I 3 ,
R3 I 3 = R5 I 5 + R4 I 4 ,
E2 = (r2 + R2 ) ⋅ I 2 + R4 I 4 ,
The solution of this system reads
I k = ∆ k / ∆ , for k=1,2,…,5,
where
(I)
(II)
(III)
(6)
(7)
∆1= R4E1R5 − R3R4E2 +R3R4E1+R4E1r2+R4E1R2+r2R5E1+R2R5E1+ E1R3r2+E1R3R2,
∆2=E2R5R1+r1R3E2+R1R3E2+E2R3R5+E2R5r1+R3R4E2+r1R4E2+R1R4E2-R3R4E1
∆3=r1R4E2+R1R4E2+R4E1R5+R4E1r2+R4E1R2+r2R5E1+R2R5E1
∆4=E1R3r2+E2R5R1+r1R3E2+R1R3E2+E2R3R5+E2R5r1+E1R3R2
∆5=R3R4E2+r1R4E2+R1R4E2 − R3R4E1-E1R3r2 − E1R3R2
and
∆=R3R4R5+R3R4r2+R3R4R2+R3R5r2+R3R5R2+r1R4R5+r1R4R3+r1R4r2+r1R4R2+r1R5r2+r1R5R2+
r1R3r2+r1R3R2+R1R4R5+R1R4R3+R1R4r2+R1R4R2+R1R5r2+R1R5R2+R1R3r2+R1R3R2
Look at this solution and imagine the typical student reaction. Imagine also the teacher effort in
deriving this solution. What you feel, the student feels too. This is why such a solution is less
probable to become the object of teaching in high schools. This kind of solution is usually called
a literal solution. Deriving such a solution is time consuming and has less teaching results. The
students become quickly bored in watching the teacher effort. It is naturally they think like that:
"What a boring lecture! I hope the teacher assumes that us will never be able to do such a task.
Maybe during this boring lecture I can do some other interesting things." As the reader probably
knows: "If something is boring, it is very difficult to do." Therefore, during physics lectures,
boring moments like this should be avoided as much as possible. Also, if possible, the literal
solution should be avoided.
In practice, we proceed with numbers from the very beginning. Numbers can be reduced,
simplified, and finally, the mathematical effort is considerably reduced. Even so, solving a
system derived directly from Kirchhoff's laws is time consuming.
Our problem has been conceived to have a nice numerical solution:
I1 = 4mA, I2 = 1mA, I3 = 3mA, I4 =2mA and I5 = 1mA.
(8)
Of course, as you probably noticed, the problem has a nice numerical solution:
Suppose the student finishes his homework and he/she fails in finding the right answer. What a
common student thinks in this particular moment looks like this: "I spent a lot of time to
understand the method, I did my best in applying it, I wrote, and solved the system. Now, there
must be a mistake, but where, I have no idea.
The steps in applying this method are:
•
The directions of currents are specified in figure 3.
•
•
•
Since node C connects the most branches, it will be used as reference node.
KCL system is given by (5).
Before writing the equations for currents, we must use proper units for measuring the
currents and the resistors. Here, we used mA, V, and kΩ. This way, the involved numbers
have less digits. After minor calculations (for instance, 1.99 + 0.01 =2 of equivalent
resistance in branch 2) the equations of branch currents in terms of node voltages are
derived
I1 = (10 − VA ) / 11 ,
I 2 = (4 − VB ) / 2 ,
I 3 = VA / 2 ,
I 4 = VB / 1 ,
I 5 = (VA − VB ) / 4 .
•
(9)
After substituting these currents in (5) the following system is derived
10 − VA VA VA − VB
=
+
,
1
2
4
VB 4 − VB VA − VB
=
+
.
1
2
4
•
•
The solution of the above system is V A = 6V and VB = 2V .
After substituting these voltages in (9), we get our “nice” solution (8) will be discovered.
Undoubtedly, such a method is better “tolerated” by students. This is a great relief both for
teacher and students. But we can do much better, as our method proves.
Simplifications. The equivalent resistances of branches 1 and 2 were computed and
placed near the nodes A and B, respectively (see figure 4). These locations are appropriate
for the needs of Millman's theorem.
A I5 4kΩ
B 2kΩ I2 F
D I1 1kΩ
I4
I3
1kΩ
10V
2kΩ
•
C
4V
Fig. 4. Following the requirements of Millman's theorem, two nodes, D and F, were labeled. With
respect to node C, their voltages are 10V and 4V, respectively.
•
•
•
•
Node C has been chosen as reference (see the reason in BCM).
To apply the Millman's theorem, two nodes, D and F, have been labeled. With respect to
the reference node, C, the voltages of these nodes are, 10V and 4V, respectively. When
applied to nodes A and B, the Millman's theorem yields to the following system
10 VB
+
4 ,
VA = 1
1 1 1
+ +
1 2 4
4 VA
+
VB = 2 4 ,
1 1 1
+ +
2 1 4
Nice look, don't you think?
It is easy to see that V A = 6V and VB = 2V is the solution of the above system.
This point forward, the branch currents are calculated in a straightforward manner, using
the Ohm's law (see figure 5).
10V I1 1kΩ
6V I5 4kΩ
2kΩ I2 4V
I4
1kΩ
2kΩ
I3
10V
2V
4V
C
Fig. 5. Last step. Deriving branch currents using Ohm's law.
Indeed, at this step, the students can derive numerical values for branch currents using the Ohm's
law only. For instance, I1 = (10 − 6)V / 1kΩ = 4 mA . This way, we come across the “nice”
solution. We hope that this example suffices to emphasize the power of our method.
Our method is particularly efficient because it transforms a complex problem into a set of
small sub-problems, each of which requiring less effort and time.
Also, our method allows for increasing the time allocated to major concepts in the
domain, instead of looking for the solution of a large system of equations. It also contributes to
developing the algorithmic thinking of students, while preparing them for jobs in many
engineering fields. With much less effort involved, even problem solving can become funny.
Actually, all the methods and theorems involved in circuit analysis are very old by now.
After such a long time passed from their discovery, reconsidering them is a necessity as the
references [4, 5] prove.
[1] G. Rizzoni, Principles and Applications of Electrical Engineering, Fourth Edition, McGraw
Hill, 2002
[2] J. Millman, A Useful Network Theorem, Proc. Inst. of Radio Engineers 28: 413, 1940.
[3] V. Nerguizian, M. Rafaf, C. Nerguizian, Electric and electronic circuit analysis with Millman
theorem, 9th WSEAS International Conference on CIRCUITS, July 11-13, 2005, pp 497-091
[4] D.H. Johnson. Origins of the Equivalent Circuit Concept: The Voltage-Source Equivalent.
Proc. IEEE, 91: 636-640, 2003.
[5] D.H. Johnson. Origins of the Equivalent Circuit Concept: The Current-Source Equivalent.
Proc. IEEE, 91: 817-821, 2003.