Download CSE 477. VLSI Systems Design

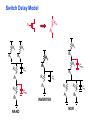
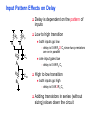
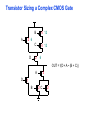
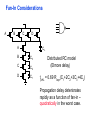
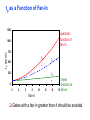
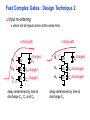
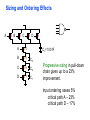
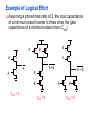
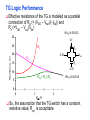
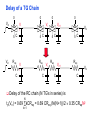
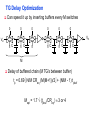
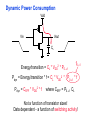
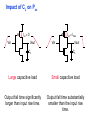
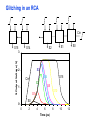
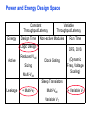
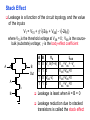
Review: Designing Inverters for Performance

Reduce CL




Increase W/L ratio of the transistor



the most powerful and effective performance optimization
tool in the hands of the designer
watch out for self-loading!
Increase VDD


internal diffusion capacitance of the gate itself
interconnect capacitance
fanout
only minimal improvement in performance at the cost of
increased energy dissipation
Slope engineering - keeping signal rise and fall times
smaller than or equal to the gate propagation delays
and of approximately equal values


good for performance
good for power consumption
Switch Delay Model
Req
A
A
Rp
A
Rp
Rp
B
Rn
Rp
B
NAND
Rp
A
CL
Cint
A
Rn
A
Rn
B
A
Cint
CL
Rn
Rn
A
B
INVERTER
NOR
CL
Input Pattern Effects on Delay
Rp
A
Rp

Delay is dependent on the pattern of
inputs

Low to high transition

B
Rn
- delay is 0.69 Rp/2 CL since two p-resistors
are on in parallel
CL

A
Rn
both inputs go low
one input goes low
- delay is 0.69 Rp CL
Cint

High to low transition

B
both inputs go high
- delay is 0.69 2Rn CL

Adding transistors in series (without
sizing) slows down the circuit
Delay Dependence on Input Patterns
2-input NAND with
NMOS = 0.5m/0.25 m
PMOS = 0.75m/0.25 m
CL = 10 fF
3
A=B=10
2.5
2
A=1 0, B=1
Voltage, V
1.5
A=1, B=10
1
0.5
0
-0.5
0
100
200
time, psec
300
400
Input Data
Delay
Pattern
(psec)
A=B=01
69
A=1, B=01
62
A= 01, B=1
50
A=B=10
35
A=1, B=10
76
A= 10, B=1
57
Transistor Sizing a Complex CMOS Gate
A
B
4 12
C
4 12
2 6
D
2
6
OUT = !(D + A • (B + C))
A
D
2
1
B
2C
2
Fan-In Considerations
A
B
C
D
A
CL
B
C3
C
C2
D
C1
Distributed RC model
(Elmore delay)
tpHL = 0.69 Reqn(C1+2C2+3C3+4CL)
Propagation delay deteriorates
rapidly as a function of fan-in –
quadratically in the worst case.
tp as a Function of Fan-In
1250
quadratic
function of
fan-in
tp (psec)
1000
750
tpH
500
tp
L
250
tpL
H
0
2
4
6
8
10
12
14
linear
function of
16 fan-in
fan-in
 Gates with a fan-in greater than 4 should be avoided.
Fast Complex Gates: Design Technique 1

Transistor sizing


as long as fan-out capacitance dominates
Progressive sizing
InN
CL
MN
In3
M3
C3
In2
M2
C2
In1
M1
Distributed RC line
C1
M1 > M2 > M3 > … > MN
(the fet closest to the output
should be the smallest)
Can reduce delay by more
than 20%; decreasing gains
as technology shrinks
Fast Complex Gates: Design Technique 2

Input re-ordering

when not all inputs arrive at the same time
critical path
In3 1 M3
charged
CL
In2 1 M2
C2 charged
In1
M1
01
C1 charged
delay determined by time to
discharge CL, C1 and C2
critical path
01
In1
M3
CLcharged
In2 1 M2
C2 discharged
In3 1 M1
C1 discharged
delay determined by time to
discharge CL
Sizing and Ordering Effects
A
3 B
3 C
3 D
A
44
B
45
C
46
C2
D
47
C1
3
CL= 100 fF
C3
Progressive sizing in pull-down
chain gives up to a 23%
improvement.
Input ordering saves 5%
critical path A – 23%
critical path D – 17%
Fast Networks: Design Technique 5 - Logical Effort

The optimum fan-out for a chain of N inverters driving a
load CL is
N
f = (CL/Cin)


so, if we can, keep the fan-out per stage around 4.
Can the same approach (logical effort) be used for any
combinational circuit?

For a complex gate, we expand the inverter equation
tp = tp0 (1 + Cext/ Cg) = tp0 (1 + f/)
to
tp = tp0 (p + g f/)
- tp0 is the intrinsic delay of an inverter
- f is the effective fan-out (Cext/Cg) – also called the electrical effort
- p is the ratio of the instrinsic (unloaded) delay of the complex gate and
a simple inverter (a function of the gate topology and layout style)
- g is the logical effort
Intrinsic Delay Term, p

The more involved the structure of the complex gate, the
higher the intrinsic delay compared to an inverter
Gate Type
p
Inverter
1
n-input NAND
n
n-input NOR
n
n-way mux
2n
XOR, XNOR
n 2n-1
Ignoring second order
effects such as internal
node capacitances
Logical Effort Term, g

g represents the fact that, for a given load, complex gates
have to work harder than an inverter to produce a similar
(speed) response

the logical effort of a gate tells how much worse it is at producing
an output current than an inverter (how much more input
capacitance a gate presents to deliver it same output current)
Gate Type
g (for 1 to 4 input gates)
1
2
3
4
NAND
4/3
5/3
(n+2)/3
NOR
5/3
7/3
(2n+1)/3
mux
2
2
2
XOR
4
12
Inverter
1
Example of Logical Effort

Assuming a pmos/nmos ratio of 2, the input capacitance
of a minimum-sized inverter is three times the gate
capacitance of a minimum-sized nmos (Cunit)
A
A
A
2 B
2
2
1
Cunit = 3
A
B
4
A
4
A•B
A
2
B
2
Cunit = 4
A+B
A
1
B
Cunit = 5
1
Delay as a Function of Fan-Out

The slope of the line is
the logical effort of the
gate

The y-axis intercept is
the intrinsic delay

Can adjust the delay by
adjusting the effective
fan-out (by sizing) or by
choosing a gate with a
different logical effort

Gate effort: h = fg
7
normalized delay
6
5
4
3
effort delay
2
1
intrinsic delay
0
0
1
2
3
4
5
fan-out f
Path Delay of Complex Logic Gate Network

Total path delay through a combinational logic block
tp =  tp,j = tp0 (pj + (fj gj)/ )

So, the minimum delay through the path determines that
each stage should bear the same gate effort
f1g1 = f2g2 = . . . = fNgN

Consider optimizing the delay through the logic network
1
a
b
c
CL 5
how do we determine a, b, and c sizes?
Path Delay Equation Derivation

The path logical effort, G =  gi

And the path effective fan-out (path electrical effort) is
F = CL/g1

The branching effort accounts for fan-out to other gates
in the network
b = (Con-path + Coff-path)/Con-path

The path branching effort is then B =  bi

And the total path effort is then H = GFB

So, the minimum delay through the path is
N
D = tp0 ( pj + (N H)/ )
Path Delay of Complex Logic Gates, con’t

For gate i in the chain, its size is determined by
i-1
si = (g1 s1)/gi  (fj/bj)
j=1
1

a
b
c
CL 5
For this network




F = CL/Cg1 = 5
G = 1 x 5/3 x 5/3 x 1 = 25/9
B = 1 (no branching)
4
H = GFB = 125/9, so the optimal stage effort is H = 1.93
- Fan-out factors are f1=1.93, f2=1.93 x 3/5 = 1.16, f3 = 1.16, f4 = 1.93

So the gate sizes are a = f1g1/g2 = 1.16, b = f1f2g1/g3 = 1.34 and
c = f1f2f3g1/g4 = 2.60
Fast Complex Gates: Design Technique 6

Reducing the voltage swing
tpHL = 0.69 (3/4 (CL VDD)/ IDSATn )
= 0.69 (3/4 (CL Vswing)/ IDSATn )



linear reduction in delay
also reduces power consumption
requires use of “sense amplifiers” on the receiving end to
restore the signal level (will look at their design when covering
memory design)
TG Logic Performance

Effective resistance of the TG is modeled as a parallel
connection of Rp (= (VDD – Vout)/(-IDp)) and
Rn (=VDD – Vout)/IDn)
W/Lp=0.50/0.25
30
0V
25
Rn
Resistance, k
20
Rp
2.5V
Rp
Vout
Rn
15
2.5V
10
Req = Rn || Rp
5
W/Ln=0.50/0.25
0
0

1
2
So, the assumption that the TG switch has a constant
resistive value, Req, is acceptable
Delay of a TG Chain
0
0
Vin
0
V
0
Vi
Vi+1
VN
1
5 C
Vin
Req
5 C
Req
V
5 C
Vi
Req
5 C
Vi+1
Req
VN
1
C

C
C
C
Delay of the RC chain (N TG’s in series) is
N
tp(Vn) = 0.69 kCReq = 0.69 CReq (N(N+1))/2  0.35 CReqN2
k=1
TG Delay Optimization

Can speed it up by inserting buffers every M switches
0
0
0
0
0
0
VN
Vin
5 C
5 C
5
5 C
5 C
5 C
M

Delay of buffered chain (M TG’s between buffer)
tp = 0.69 N/M CReq (M(M+1))/2 + (N/M - 1) tpbuf
Mopt = 1.7  (tpbuf/CReq )  3 or 4
Why Power Matters

Packaging costs

Power supply rail design

Chip and system cooling costs

Noise immunity and system reliability

Battery life (in portable systems)

Environmental concerns


Office equipment accounted for 5% of total US commercial
energy usage in 1993
Energy Star compliant systems
Chip Power Density Distribution
Al-SiC+ Epoxy Die Attach
WillametteMap
Power Distribution
Power
On-Die Temperature
110
250
100
100
200-250
90
150-200
100-150
80
50-100
0-50
70
60
Temperature (C)
150
Heat Flux (W/cm2)
200
50
50
0
40

Power density is not uniformly distributed across the chip

Silicon is not a good heat conductor

Max junction temperature is determined by hot-spots
 Impact on packaging, w.r.t. cooling
Power and Energy Figures of Merit

Power consumption in Watts


Peak power




determines power ground wiring designs
sets packaging limits
impacts signal noise margin and reliability analysis
Energy efficiency in Joules


determines battery life in hours
rate at which power is consumed over time
Energy = power * delay


Joules = Watts * seconds
lower energy number means less power to perform a
computation at the same frequency
Power versus Energy
Power is height of curve
Watts
Lower power design could simply be slower
Approach 1
Approach 2
Watts
time
Energy is area under curve
Two approaches require the same energy
Approach 1
Approach 2
time
PDP and EDP
Power-delay product (PDP) = Pav * tp = (CLVDD2)/2



PDP is the average energy consumed per switching event
(Watts * sec = Joule)
lower power design could simply be a slower design
Energy-delay product (EDP) = PDP * tp = Pav * tp2


EDP is the average energy
consumed multiplied by the
computation time required
takes into account that one
can trade increased delay
for lower energy/operation
(e.g., via supply voltage
scaling that increases delay,
but decreases energy
consumption)
Energy-Delay (normalized)

15
energy-delay
10
energy
5
delay
0
0.5

allows one to understand tradeoffs better
1
1.5
Vdd (V)
2
2.5
Understanding Tradeoffs

Which design is the “best” (fastest, coolest, both) ?
Lower
EDP
b
c
d
1/Delay
better
a
CMOS Energy & Power Equations
E = CL VDD2 P01 + tsc VDD Ipeak P01 + VDD
Ileakage
f01 = P01 * fclock
P = CL VDD2 f01 + tscVDD Ipeak f01 + VDD Ileakage
Dynamic
power
Short-circuit
power
Leakage
power
Dynamic Power Consumption
Vdd
Vin
Vout
CL
Energy/transition = CL *
VDD2
* P01
f01
Pdyn = Energy/transition * f = CL * VDD2 * P01 * f
Pdyn = CEFF * VDD2 * f
where CEFF = P01 CL
Not a function of transistor sizes!
Data dependent - a function of switching activity!
Lowering Dynamic Power
Capacitance:
Function of fan-out,
wire length, transistor
sizes
Supply Voltage:
Has been dropping
with successive
generations
Pdyn = CL VDD2 P01 f
Activity factor:
How often, on average,
do wires switch?
Clock frequency:
Increasing…
Short Circuit Power Consumption
Vin
Isc
Vout
CL
Finite slope of the input signal causes a direct
current path between VDD and GND for a short
period of time during switching when both the
NMOS and PMOS transistors are conducting.
Short Circuit Currents Determinates
Esc = tsc VDD Ipeak P01
Psc = tsc VDD Ipeak f01

Duration and slope of the input signal, tsc
 Ipeak


determined by
the saturation current of the P and N transistors which
depend on their sizes, process technology, temperature, etc.
strong function of the ratio between input and output slopes
- a function of CL
Impact of CL on Psc
Isc  0
Vin
Isc  Imax
Vout
CL
Vin
Vout
CL
Large capacitive load
Small capacitive load
Output fall time significantly
larger than input rise time.
Output fall time substantially
smaller than the input rise
time.
Ipeak as a Function of CL
2.5
x 10-4
CL = 20 fF
2
When load capacitance
is small, Ipeak is large.
1.5
CL = 100 fF
1
0.5
0
0
-0.5
2
Short circuit dissipation
is minimized by
CL = 500 fF
matching the rise/fall
times of the input and
4
6
x 10-10 output signals - slope
engineering.
time (sec)
500 psec input slope
Psc as a Function of Rise/Fall Times
8
When load capacitance
is small (tsin/tsout > 2 for
VDD > 2V) the power is
dominated by Psc
7
VDD= 3.3 V
6
5
4
VDD = 2.5 V
3
2
1
VDD = 1.5V
0
0
2
tsin/tsou
If VDD < VTn + |VTp| then
Psc is eliminated since
both devices are never
on at the same time.
4
t
W/Lp = 1.125 m/0.25 m
W/Ln = 0.375 m/0.25 m
CL = 30 fF
normalized wrt zero input
rise-time dissipation
Leakage (Static) Power Consumption
VDD Ileakage
Vout
Drain junction
leakage
Gate leakage
Sub-threshold current
Sub-threshold current is the dominant factor.
All increase exponentially with temperature!
Leakage as a Function of VT

Continued scaling of supply voltage and the subsequent
scaling of threshold voltage will make subthreshold
conduction a dominate component of power dissipation.
10-2
ID (A)

10-7
VT=0.4V
VT=0.1V
10-12
0
0.2
0.4
0.6
VGS (V)
0.8
1
An 90mV/decade VT
roll-off - so each
255mV increase in
VT gives 3 orders of
magnitude reduction
in leakage (but
adversely affects
performance)
TSMC Processes Leakage and VT
CL018
G
CL018
LP
CL018
ULP
CL018
HS
CL015
HS
CL013
HS
Vdd
1.8 V
1.8 V
1.8 V
2V
1.5 V
1.2 V
Tox (effective)
42 Å
42 Å
42 Å
42 Å
29 Å
24 Å
Lgate
0.16 m
0.16 m
0.18 m
0.13 m
0.11 m
0.08 m
IDSat (n/p)
(A/m)
600/260
500/180
320/130
780/360
860/370
920/400
20
1.60
0.15
300
1,800
13,000
0.42 V
0.63 V
0.73 V
0.40 V
0.29 V
0.25 V
30
22
14
43
52
80
Ioff (leakage)
(A/m)
VTn
FET Perf.
(GHz)
From MPR, 2000
Exponential Increase in Leakage Currents
10000
Ileakage(nA/m)
1000
0.25
0.18
0.13
0.1
100
10
1
30
40
50
60
70
80
Temp(C)
90
100
110
From De,1999
Review: Energy & Power Equations
E = CL VDD2 P01 + tsc VDD Ipeak P01 + VDD
Ileakage
f01 = P01 * fclock
P = CL VDD2 f01 + tscVDD Ipeak f01 + VDD Ileakage
Dynamic power
(~90% today and
decreasing
relatively)
Short-circuit
power
(~8% today and
decreasing
absolutely)
Leakage power
(~2% today and
increasing)
Power and Energy Design Space
Constant
Throughput/Latency
Energy
Design Time
Variable
Throughput/Latency
Non-active Modules
Logic Design
Active
Reduced Vdd
Run Time
DFS, DVS
Clock Gating
Sizing
Multi-Vdd
(Dynamic
Freq, Voltage
Scaling)
Sleep Transistors
Leakage
+ Multi-VT
Multi-Vdd
Variable VT
+ Variable VT
Dynamic Power as a Function of Device Size
Device sizing affects dynamic energy consumption


The optimal gate sizing factor
(f) for dynamic energy is
smaller than the one for
performance, especially for
large F’s


gain is largest for networks with large overall effective fan-outs (F
= CL/Cg,1)
e.g., for F=20,
fopt(energy) = 3.53 while
fopt(performance) = 4.47
If energy is a concern avoid
oversizing beyond the
optimal
1.5
F=1
normalized energy

F=2
1
F=5
0.5
F=10
F=20
0
1
2
3
4
f
5
6
From Nikolic, UCB
7
Dynamic Power Consumption is Data Dependent

Switching activity, P01, has two components


A static component – function of the logic topology
A dynamic component – function of the timing behavior (glitching)
2-input NOR Gate
A
B
Out
0
0
1
0
1
0
1
0
0
1
1
0
Static transition probability
P01 = Pout=0 x Pout=1
= P0 x (1-P0)
With input signal probabilities
PA=1 = 1/2
PB=1 = 1/2
NOR static transition probability
= 3/4 x 1/4 = 3/16
NOR Gate Transition Probabilities

Switching activity is a strong function of the input signal
statistics

PA and PB are the probabilities that inputs A and B are one
A
B
0
A
B
CL
PA
1 0
PB
1
P01 = P0 x P1 = (1-(1-PA)(1-PB)) (1-PA)(1-PB)
Transition Probabilities for Some Basic Gates
NOR
OR
NAND
AND
XOR
P01 = Pout=0 x Pout=1
(1 - (1 - PA)(1 - PB)) x (1 - PA)(1 - PB)
(1 - PA)(1 - PB) x (1 - (1 - PA)(1 - PB))
PAPB x (1 - PAPB)
(1 - PAPB) x PAPB
(1 - (PA + PB- 2PAPB)) x (PA + PB- 2PAPB)
0.5 A
0.5 B
X
Z
For X: P01 = P0 x P1 = (1-PA) PA
= 0.5 x 0.5 = 0.25
For Z: P01 = P0 x P1 = (1-PXPB) PXPB
= (1 – (0.5 x 0.5)) x (0.5 x 0.5) = 3/16
Inter-signal Correlations

Determining switching activity is complicated by the fact
that signals exhibit correlation in space and time

reconvergent fan-out
(1-0.5)(1-0.5)x(1-(1-0.5)(1-0.5)) = 3/16
0.5
A
0.5
B
X
Z
(1- 3/16 x 0.5) x (3/16 x 0.5) = 0.085
Reconvergent
P(Z=1) = P(B=1) & P(A=1 | B=1)

Have to use conditional probabilities
Logic Restructuring

Logic restructuring: changing the topology of a logic
network to reduce transitions
AND: P01 = P0 x P1 = (1 - PAPB) x PAPB
0.5
A
B
0.5
(1-0.25)*0.25 = 3/16
7/64
W
X
15/256
C
F
0.5
D
0.5
0.5 A
0.5 B
0.5
C
0.5 D
3/16
Y
15/256
F
Z
3/16
Chain implementation has a lower overall switching activity
than the tree implementation for random inputs
Ignores glitching effects
Input Ordering
(1-0.5x0.2)x(0.5x0.2)=0.09
0.5
A
B
0.2
X
C
0.1
F
0.2
B
C
0.1
(1-0.2x0.1)x(0.2x0.1)=0.0196
X
A
0.5
F
Beneficial to postpone the introduction of signals with a
high transition rate (signals with signal probability
close to 0.5)
Glitching in Static CMOS Networks

Gates have a nonzero propagation delay resulting in
spurious transitions or glitches (dynamic hazards)

glitch: node exhibits multiple transitions in a single cycle before
settling to the correct logic value
A
B
X
Z
C
ABC
101
000
X
Z
Unit Delay
Glitching in an RCA
Cin
S14
S15
S0
S1
S2
S Output Voltage (V)
3
S3
2
S4
Cin
S2
S15
S5
1
S10
S1
S0
0
0
2
4
6
Time (ps)
8
10
12
Balanced Delay Paths to Reduce Glitching

Glitching is due to a mismatch in the path lengths in
the logic network; if all input signals of a gate change
simultaneously, no glitching occurs
0
0
0
0
F1
0
0
1
F1
1
F2 2
F3
0
0
F3
F2
1
So equalize the lengths of timing paths through logic
Power and Energy Design Space
Constant
Throughput/Latency
Energy
Design Time
Variable
Throughput/Latency
Non-active Modules
Logic Design
Active
Reduced Vdd
Run Time
DFS, DVS
Clock Gating
Sizing
Multi-Vdd
(Dynamic
Freq, Voltage
Scaling)
Sleep Transistors
Leakage
+ Multi-VT
Multi-Vdd
Variable VT
+ Variable VT
Dynamic Power as a Function of VDD


Decreasing the VDD
decreases dynamic
energy consumption
(quadratically)
But, increases gate
delay (decreases
performance)
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
VDD (V)

Determine the critical path(s) at design time and use high
VDD for the transistors on those paths for speed. Use a
lower VDD on the other gates, especially those that drive
large capacitances (as this yields the largest energy
benefits).
Multiple VDD Considerations

How many VDD? – Two is becoming common


Many chips already have two supplies (one for core and one for I/O)
When combining multiple supplies, level converters are
required whenever a module at the lower supply drives a
gate at the higher supply (step-up)

If a gate supplied with VDDL drives a gate at VDDH, the PMOS never
turns off
V
- The cross-coupled PMOS transistors
do the level conversion
- The NMOS transistor operate on a
reduced supply


Vin
DDH
VDDL
Vout
Level converters are not needed
for a step-down change in voltage
Overhead of level converters can be mitigated by doing conversions
at register boundaries and embedding the level conversion inside
the flipflop (see Figure 11.47)
Dual-Supply Inside a Logic Block

Minimum energy consumption is achieved if all logic
paths are critical (have the same delay)

Clustered voltage-scaling


Each path starts with VDDH and switches to VDDL (gray logic
gates) when delay slack is available
Level conversion is done in the flipflops at the end of the paths
Power and Energy Design Space
Constant
Throughput/Latency
Energy
Design Time
Variable
Throughput/Latency
Non-active Modules
Logic Design
Active
Reduced Vdd
Run Time
DFS, DVS
Clock Gating
Sizing
Multi-Vdd
(Dynamic
Freq, Voltage
Scaling)
Sleep Transistors
Leakage
+ Multi-VT
Multi-Vdd
Variable VT
+ Variable VT
Stack Effect

Leakage is a function of the circuit topology and the value
of the inputs
VT = VT0 + (|-2F + VSB| - |-2F|)
where VT0 is the threshold voltage at VSB = 0; VSB is the sourcebulk (substrate) voltage;  is the body-effect coefficient
A
A
0
0
1
1
B
Out
A
VX
B
B
0
1
0
1
VX
VT ln(1+n)
0
VDD-VT
0
ISUB
VGS=VBS= -VX
VGS=VBS=0
VGS=VBS=0
VSG=VSB=0

Leakage is least when A = B = 0

Leakage reduction due to stacked
transistors is called the stack effect
Short Channel Factors and Stack Effect

In short-channel devices, the subthreshold leakage
current depends on VGS,VBS and VDS. The VT of a
short-channel device decreases with increasing VDS
due to DIBL (drain-induced barrier loading).



Typical values for DIBL are 20 to 150mV change in VT per
voltage change in VDS so the stack effect is even more
significant for short-channel devices.
VX reduces the drain-source voltage of the top nfet, increasing
its VT and lowering its leakage
For our 0.25 micron technology, VX settles to ~100mV in
steady state so VBS = -100mV and VDS = VDD -100mV
which is 20 times smaller than the leakage of a device
with VBS = 0mV and VDS = VDD

Reducing the VT
increases the subthreshold leakage
current (exponentially)


90mV reduction in VT
increases leakage by an
order of magnitude
But, reducing VT
decreases gate delay
(increases performance)
ID (A)
Leakage as a Function of Design Time VT
VT=0.4V
VT=0.1V
0
0.2
0.4
0.6
0.8
1
VGS (V)

Determine the critical path(s) at design time and use low
VT devices on the transistors on those paths for speed.
Use a high VT on the other logic for leakage control.

A careful assignment of VT’s can reduce the leakage by as much
as 80%
Dual-Thresholds Inside a Logic Block

Minimum energy consumption is achieved if all logic
paths are critical (have the same delay)

Use lower threshold on timing-critical paths


Assignment can be done on a per gate or transistor basis; no
clustering of the logic is needed
No level converters are needed
Variable VT (ABB) at Run Time

VT = VT0 + (|-2F + VSB| - |-2F|)
For an n-channel device, the substrate is normally tied
to ground (VSB = 0)

 A negative
bias on VSB
causes VT to increase
 Adjusting
the substrate
bias at run time is called
adaptive body-biasing
(ABB)
Requires a dual well fab
process

0.9
0.85
0.8
0.75
0.7
0.65
0.6
0.55
0.5
0.45
0.4
-2.5
-2
-1.5
-1
VSB (V)
-0.5
0