* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download CSE 477. VLSI Systems Design
Immunity-aware programming wikipedia , lookup
Control system wikipedia , lookup
Spectral density wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Power inverter wikipedia , lookup
Solar micro-inverter wikipedia , lookup
Alternating current wikipedia , lookup
Distribution management system wikipedia , lookup
Mains electricity wikipedia , lookup
Power engineering wikipedia , lookup
Voltage optimisation wikipedia , lookup
Distributed generation wikipedia , lookup
Opto-isolator wikipedia , lookup
Buck converter wikipedia , lookup
Life-cycle greenhouse-gas emissions of energy sources wikipedia , lookup
Power electronics wikipedia , lookup
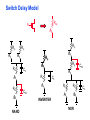
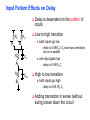
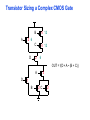
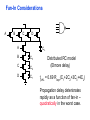
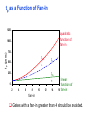
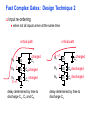
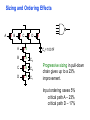
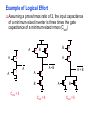
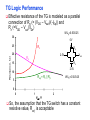
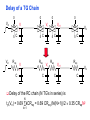
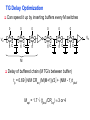
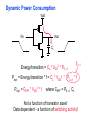
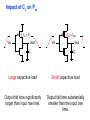
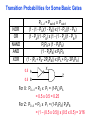
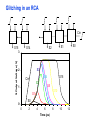
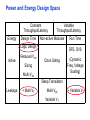
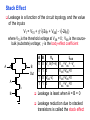
Review: Designing Inverters for Performance Reduce CL Increase W/L ratio of the transistor the most powerful and effective performance optimization tool in the hands of the designer watch out for self-loading! Increase VDD internal diffusion capacitance of the gate itself interconnect capacitance fanout only minimal improvement in performance at the cost of increased energy dissipation Slope engineering - keeping signal rise and fall times smaller than or equal to the gate propagation delays and of approximately equal values good for performance good for power consumption Switch Delay Model Req A A Rp A Rp Rp B Rn Rp B NAND Rp A CL Cint A Rn A Rn B A Cint CL Rn Rn A B INVERTER NOR CL Input Pattern Effects on Delay Rp A Rp Delay is dependent on the pattern of inputs Low to high transition B Rn - delay is 0.69 Rp/2 CL since two p-resistors are on in parallel CL A Rn both inputs go low one input goes low - delay is 0.69 Rp CL Cint High to low transition B both inputs go high - delay is 0.69 2Rn CL Adding transistors in series (without sizing) slows down the circuit Delay Dependence on Input Patterns 2-input NAND with NMOS = 0.5m/0.25 m PMOS = 0.75m/0.25 m CL = 10 fF 3 A=B=10 2.5 2 A=1 0, B=1 Voltage, V 1.5 A=1, B=10 1 0.5 0 -0.5 0 100 200 time, psec 300 400 Input Data Delay Pattern (psec) A=B=01 69 A=1, B=01 62 A= 01, B=1 50 A=B=10 35 A=1, B=10 76 A= 10, B=1 57 Transistor Sizing a Complex CMOS Gate A B 4 12 C 4 12 2 6 D 2 6 OUT = !(D + A • (B + C)) A D 2 1 B 2C 2 Fan-In Considerations A B C D A CL B C3 C C2 D C1 Distributed RC model (Elmore delay) tpHL = 0.69 Reqn(C1+2C2+3C3+4CL) Propagation delay deteriorates rapidly as a function of fan-in – quadratically in the worst case. tp as a Function of Fan-In 1250 quadratic function of fan-in tp (psec) 1000 750 tpH 500 tp L 250 tpL H 0 2 4 6 8 10 12 14 linear function of 16 fan-in fan-in Gates with a fan-in greater than 4 should be avoided. Fast Complex Gates: Design Technique 1 Transistor sizing as long as fan-out capacitance dominates Progressive sizing InN CL MN In3 M3 C3 In2 M2 C2 In1 M1 Distributed RC line C1 M1 > M2 > M3 > … > MN (the fet closest to the output should be the smallest) Can reduce delay by more than 20%; decreasing gains as technology shrinks Fast Complex Gates: Design Technique 2 Input re-ordering when not all inputs arrive at the same time critical path In3 1 M3 charged CL In2 1 M2 C2 charged In1 M1 01 C1 charged delay determined by time to discharge CL, C1 and C2 critical path 01 In1 M3 CLcharged In2 1 M2 C2 discharged In3 1 M1 C1 discharged delay determined by time to discharge CL Sizing and Ordering Effects A 3 B 3 C 3 D A 44 B 45 C 46 C2 D 47 C1 3 CL= 100 fF C3 Progressive sizing in pull-down chain gives up to a 23% improvement. Input ordering saves 5% critical path A – 23% critical path D – 17% Fast Networks: Design Technique 5 - Logical Effort The optimum fan-out for a chain of N inverters driving a load CL is N f = (CL/Cin) so, if we can, keep the fan-out per stage around 4. Can the same approach (logical effort) be used for any combinational circuit? For a complex gate, we expand the inverter equation tp = tp0 (1 + Cext/ Cg) = tp0 (1 + f/) to tp = tp0 (p + g f/) - tp0 is the intrinsic delay of an inverter - f is the effective fan-out (Cext/Cg) – also called the electrical effort - p is the ratio of the instrinsic (unloaded) delay of the complex gate and a simple inverter (a function of the gate topology and layout style) - g is the logical effort Intrinsic Delay Term, p The more involved the structure of the complex gate, the higher the intrinsic delay compared to an inverter Gate Type p Inverter 1 n-input NAND n n-input NOR n n-way mux 2n XOR, XNOR n 2n-1 Ignoring second order effects such as internal node capacitances Logical Effort Term, g g represents the fact that, for a given load, complex gates have to work harder than an inverter to produce a similar (speed) response the logical effort of a gate tells how much worse it is at producing an output current than an inverter (how much more input capacitance a gate presents to deliver it same output current) Gate Type g (for 1 to 4 input gates) 1 2 3 4 NAND 4/3 5/3 (n+2)/3 NOR 5/3 7/3 (2n+1)/3 mux 2 2 2 XOR 4 12 Inverter 1 Example of Logical Effort Assuming a pmos/nmos ratio of 2, the input capacitance of a minimum-sized inverter is three times the gate capacitance of a minimum-sized nmos (Cunit) A A A 2 B 2 2 1 Cunit = 3 A B 4 A 4 A•B A 2 B 2 Cunit = 4 A+B A 1 B Cunit = 5 1 Delay as a Function of Fan-Out The slope of the line is the logical effort of the gate The y-axis intercept is the intrinsic delay Can adjust the delay by adjusting the effective fan-out (by sizing) or by choosing a gate with a different logical effort Gate effort: h = fg 7 normalized delay 6 5 4 3 effort delay 2 1 intrinsic delay 0 0 1 2 3 4 5 fan-out f Path Delay of Complex Logic Gate Network Total path delay through a combinational logic block tp = tp,j = tp0 (pj + (fj gj)/ ) So, the minimum delay through the path determines that each stage should bear the same gate effort f1g1 = f2g2 = . . . = fNgN Consider optimizing the delay through the logic network 1 a b c CL 5 how do we determine a, b, and c sizes? Path Delay Equation Derivation The path logical effort, G = gi And the path effective fan-out (path electrical effort) is F = CL/g1 The branching effort accounts for fan-out to other gates in the network b = (Con-path + Coff-path)/Con-path The path branching effort is then B = bi And the total path effort is then H = GFB So, the minimum delay through the path is N D = tp0 ( pj + (N H)/ ) Path Delay of Complex Logic Gates, con’t For gate i in the chain, its size is determined by i-1 si = (g1 s1)/gi (fj/bj) j=1 1 a b c CL 5 For this network F = CL/Cg1 = 5 G = 1 x 5/3 x 5/3 x 1 = 25/9 B = 1 (no branching) 4 H = GFB = 125/9, so the optimal stage effort is H = 1.93 - Fan-out factors are f1=1.93, f2=1.93 x 3/5 = 1.16, f3 = 1.16, f4 = 1.93 So the gate sizes are a = f1g1/g2 = 1.16, b = f1f2g1/g3 = 1.34 and c = f1f2f3g1/g4 = 2.60 Fast Complex Gates: Design Technique 6 Reducing the voltage swing tpHL = 0.69 (3/4 (CL VDD)/ IDSATn ) = 0.69 (3/4 (CL Vswing)/ IDSATn ) linear reduction in delay also reduces power consumption requires use of “sense amplifiers” on the receiving end to restore the signal level (will look at their design when covering memory design) TG Logic Performance Effective resistance of the TG is modeled as a parallel connection of Rp (= (VDD – Vout)/(-IDp)) and Rn (=VDD – Vout)/IDn) W/Lp=0.50/0.25 30 0V 25 Rn Resistance, k 20 Rp 2.5V Rp Vout Rn 15 2.5V 10 Req = Rn || Rp 5 W/Ln=0.50/0.25 0 0 1 2 So, the assumption that the TG switch has a constant resistive value, Req, is acceptable Delay of a TG Chain 0 0 Vin 0 V 0 Vi Vi+1 VN 1 5 C Vin Req 5 C Req V 5 C Vi Req 5 C Vi+1 Req VN 1 C C C C Delay of the RC chain (N TG’s in series) is N tp(Vn) = 0.69 kCReq = 0.69 CReq (N(N+1))/2 0.35 CReqN2 k=1 TG Delay Optimization Can speed it up by inserting buffers every M switches 0 0 0 0 0 0 VN Vin 5 C 5 C 5 5 C 5 C 5 C M Delay of buffered chain (M TG’s between buffer) tp = 0.69 N/M CReq (M(M+1))/2 + (N/M - 1) tpbuf Mopt = 1.7 (tpbuf/CReq ) 3 or 4 Why Power Matters Packaging costs Power supply rail design Chip and system cooling costs Noise immunity and system reliability Battery life (in portable systems) Environmental concerns Office equipment accounted for 5% of total US commercial energy usage in 1993 Energy Star compliant systems Chip Power Density Distribution Al-SiC+ Epoxy Die Attach WillametteMap Power Distribution Power On-Die Temperature 110 250 100 100 200-250 90 150-200 100-150 80 50-100 0-50 70 60 Temperature (C) 150 Heat Flux (W/cm2) 200 50 50 0 40 Power density is not uniformly distributed across the chip Silicon is not a good heat conductor Max junction temperature is determined by hot-spots Impact on packaging, w.r.t. cooling Power and Energy Figures of Merit Power consumption in Watts Peak power determines power ground wiring designs sets packaging limits impacts signal noise margin and reliability analysis Energy efficiency in Joules determines battery life in hours rate at which power is consumed over time Energy = power * delay Joules = Watts * seconds lower energy number means less power to perform a computation at the same frequency Power versus Energy Power is height of curve Watts Lower power design could simply be slower Approach 1 Approach 2 Watts time Energy is area under curve Two approaches require the same energy Approach 1 Approach 2 time PDP and EDP Power-delay product (PDP) = Pav * tp = (CLVDD2)/2 PDP is the average energy consumed per switching event (Watts * sec = Joule) lower power design could simply be a slower design Energy-delay product (EDP) = PDP * tp = Pav * tp2 EDP is the average energy consumed multiplied by the computation time required takes into account that one can trade increased delay for lower energy/operation (e.g., via supply voltage scaling that increases delay, but decreases energy consumption) Energy-Delay (normalized) 15 energy-delay 10 energy 5 delay 0 0.5 allows one to understand tradeoffs better 1 1.5 Vdd (V) 2 2.5 Understanding Tradeoffs Which design is the “best” (fastest, coolest, both) ? Lower EDP b c d 1/Delay better a CMOS Energy & Power Equations E = CL VDD2 P01 + tsc VDD Ipeak P01 + VDD Ileakage f01 = P01 * fclock P = CL VDD2 f01 + tscVDD Ipeak f01 + VDD Ileakage Dynamic power Short-circuit power Leakage power Dynamic Power Consumption Vdd Vin Vout CL Energy/transition = CL * VDD2 * P01 f01 Pdyn = Energy/transition * f = CL * VDD2 * P01 * f Pdyn = CEFF * VDD2 * f where CEFF = P01 CL Not a function of transistor sizes! Data dependent - a function of switching activity! Lowering Dynamic Power Capacitance: Function of fan-out, wire length, transistor sizes Supply Voltage: Has been dropping with successive generations Pdyn = CL VDD2 P01 f Activity factor: How often, on average, do wires switch? Clock frequency: Increasing… Short Circuit Power Consumption Vin Isc Vout CL Finite slope of the input signal causes a direct current path between VDD and GND for a short period of time during switching when both the NMOS and PMOS transistors are conducting. Short Circuit Currents Determinates Esc = tsc VDD Ipeak P01 Psc = tsc VDD Ipeak f01 Duration and slope of the input signal, tsc Ipeak determined by the saturation current of the P and N transistors which depend on their sizes, process technology, temperature, etc. strong function of the ratio between input and output slopes - a function of CL Impact of CL on Psc Isc 0 Vin Isc Imax Vout CL Vin Vout CL Large capacitive load Small capacitive load Output fall time significantly larger than input rise time. Output fall time substantially smaller than the input rise time. Ipeak as a Function of CL 2.5 x 10-4 CL = 20 fF 2 When load capacitance is small, Ipeak is large. 1.5 CL = 100 fF 1 0.5 0 0 -0.5 2 Short circuit dissipation is minimized by CL = 500 fF matching the rise/fall times of the input and 4 6 x 10-10 output signals - slope engineering. time (sec) 500 psec input slope Psc as a Function of Rise/Fall Times 8 When load capacitance is small (tsin/tsout > 2 for VDD > 2V) the power is dominated by Psc 7 VDD= 3.3 V 6 5 4 VDD = 2.5 V 3 2 1 VDD = 1.5V 0 0 2 tsin/tsou If VDD < VTn + |VTp| then Psc is eliminated since both devices are never on at the same time. 4 t W/Lp = 1.125 m/0.25 m W/Ln = 0.375 m/0.25 m CL = 30 fF normalized wrt zero input rise-time dissipation Leakage (Static) Power Consumption VDD Ileakage Vout Drain junction leakage Gate leakage Sub-threshold current Sub-threshold current is the dominant factor. All increase exponentially with temperature! Leakage as a Function of VT Continued scaling of supply voltage and the subsequent scaling of threshold voltage will make subthreshold conduction a dominate component of power dissipation. 10-2 ID (A) 10-7 VT=0.4V VT=0.1V 10-12 0 0.2 0.4 0.6 VGS (V) 0.8 1 An 90mV/decade VT roll-off - so each 255mV increase in VT gives 3 orders of magnitude reduction in leakage (but adversely affects performance) TSMC Processes Leakage and VT CL018 G CL018 LP CL018 ULP CL018 HS CL015 HS CL013 HS Vdd 1.8 V 1.8 V 1.8 V 2V 1.5 V 1.2 V Tox (effective) 42 Å 42 Å 42 Å 42 Å 29 Å 24 Å Lgate 0.16 m 0.16 m 0.18 m 0.13 m 0.11 m 0.08 m IDSat (n/p) (A/m) 600/260 500/180 320/130 780/360 860/370 920/400 20 1.60 0.15 300 1,800 13,000 0.42 V 0.63 V 0.73 V 0.40 V 0.29 V 0.25 V 30 22 14 43 52 80 Ioff (leakage) (A/m) VTn FET Perf. (GHz) From MPR, 2000 Exponential Increase in Leakage Currents 10000 Ileakage(nA/m) 1000 0.25 0.18 0.13 0.1 100 10 1 30 40 50 60 70 80 Temp(C) 90 100 110 From De,1999 Review: Energy & Power Equations E = CL VDD2 P01 + tsc VDD Ipeak P01 + VDD Ileakage f01 = P01 * fclock P = CL VDD2 f01 + tscVDD Ipeak f01 + VDD Ileakage Dynamic power (~90% today and decreasing relatively) Short-circuit power (~8% today and decreasing absolutely) Leakage power (~2% today and increasing) Power and Energy Design Space Constant Throughput/Latency Energy Design Time Variable Throughput/Latency Non-active Modules Logic Design Active Reduced Vdd Run Time DFS, DVS Clock Gating Sizing Multi-Vdd (Dynamic Freq, Voltage Scaling) Sleep Transistors Leakage + Multi-VT Multi-Vdd Variable VT + Variable VT Dynamic Power as a Function of Device Size Device sizing affects dynamic energy consumption The optimal gate sizing factor (f) for dynamic energy is smaller than the one for performance, especially for large F’s gain is largest for networks with large overall effective fan-outs (F = CL/Cg,1) e.g., for F=20, fopt(energy) = 3.53 while fopt(performance) = 4.47 If energy is a concern avoid oversizing beyond the optimal 1.5 F=1 normalized energy F=2 1 F=5 0.5 F=10 F=20 0 1 2 3 4 f 5 6 From Nikolic, UCB 7 Dynamic Power Consumption is Data Dependent Switching activity, P01, has two components A static component – function of the logic topology A dynamic component – function of the timing behavior (glitching) 2-input NOR Gate A B Out 0 0 1 0 1 0 1 0 0 1 1 0 Static transition probability P01 = Pout=0 x Pout=1 = P0 x (1-P0) With input signal probabilities PA=1 = 1/2 PB=1 = 1/2 NOR static transition probability = 3/4 x 1/4 = 3/16 NOR Gate Transition Probabilities Switching activity is a strong function of the input signal statistics PA and PB are the probabilities that inputs A and B are one A B 0 A B CL PA 1 0 PB 1 P01 = P0 x P1 = (1-(1-PA)(1-PB)) (1-PA)(1-PB) Transition Probabilities for Some Basic Gates NOR OR NAND AND XOR P01 = Pout=0 x Pout=1 (1 - (1 - PA)(1 - PB)) x (1 - PA)(1 - PB) (1 - PA)(1 - PB) x (1 - (1 - PA)(1 - PB)) PAPB x (1 - PAPB) (1 - PAPB) x PAPB (1 - (PA + PB- 2PAPB)) x (PA + PB- 2PAPB) 0.5 A 0.5 B X Z For X: P01 = P0 x P1 = (1-PA) PA = 0.5 x 0.5 = 0.25 For Z: P01 = P0 x P1 = (1-PXPB) PXPB = (1 – (0.5 x 0.5)) x (0.5 x 0.5) = 3/16 Inter-signal Correlations Determining switching activity is complicated by the fact that signals exhibit correlation in space and time reconvergent fan-out (1-0.5)(1-0.5)x(1-(1-0.5)(1-0.5)) = 3/16 0.5 A 0.5 B X Z (1- 3/16 x 0.5) x (3/16 x 0.5) = 0.085 Reconvergent P(Z=1) = P(B=1) & P(A=1 | B=1) Have to use conditional probabilities Logic Restructuring Logic restructuring: changing the topology of a logic network to reduce transitions AND: P01 = P0 x P1 = (1 - PAPB) x PAPB 0.5 A B 0.5 (1-0.25)*0.25 = 3/16 7/64 W X 15/256 C F 0.5 D 0.5 0.5 A 0.5 B 0.5 C 0.5 D 3/16 Y 15/256 F Z 3/16 Chain implementation has a lower overall switching activity than the tree implementation for random inputs Ignores glitching effects Input Ordering (1-0.5x0.2)x(0.5x0.2)=0.09 0.5 A B 0.2 X C 0.1 F 0.2 B C 0.1 (1-0.2x0.1)x(0.2x0.1)=0.0196 X A 0.5 F Beneficial to postpone the introduction of signals with a high transition rate (signals with signal probability close to 0.5) Glitching in Static CMOS Networks Gates have a nonzero propagation delay resulting in spurious transitions or glitches (dynamic hazards) glitch: node exhibits multiple transitions in a single cycle before settling to the correct logic value A B X Z C ABC 101 000 X Z Unit Delay Glitching in an RCA Cin S14 S15 S0 S1 S2 S Output Voltage (V) 3 S3 2 S4 Cin S2 S15 S5 1 S10 S1 S0 0 0 2 4 6 Time (ps) 8 10 12 Balanced Delay Paths to Reduce Glitching Glitching is due to a mismatch in the path lengths in the logic network; if all input signals of a gate change simultaneously, no glitching occurs 0 0 0 0 F1 0 0 1 F1 1 F2 2 F3 0 0 F3 F2 1 So equalize the lengths of timing paths through logic Power and Energy Design Space Constant Throughput/Latency Energy Design Time Variable Throughput/Latency Non-active Modules Logic Design Active Reduced Vdd Run Time DFS, DVS Clock Gating Sizing Multi-Vdd (Dynamic Freq, Voltage Scaling) Sleep Transistors Leakage + Multi-VT Multi-Vdd Variable VT + Variable VT Dynamic Power as a Function of VDD Decreasing the VDD decreases dynamic energy consumption (quadratically) But, increases gate delay (decreases performance) 5.5 5 4.5 4 3.5 3 2.5 2 1.5 1 0.8 1 1.2 1.4 1.6 1.8 2 2.2 2.4 VDD (V) Determine the critical path(s) at design time and use high VDD for the transistors on those paths for speed. Use a lower VDD on the other gates, especially those that drive large capacitances (as this yields the largest energy benefits). Multiple VDD Considerations How many VDD? – Two is becoming common Many chips already have two supplies (one for core and one for I/O) When combining multiple supplies, level converters are required whenever a module at the lower supply drives a gate at the higher supply (step-up) If a gate supplied with VDDL drives a gate at VDDH, the PMOS never turns off V - The cross-coupled PMOS transistors do the level conversion - The NMOS transistor operate on a reduced supply Vin DDH VDDL Vout Level converters are not needed for a step-down change in voltage Overhead of level converters can be mitigated by doing conversions at register boundaries and embedding the level conversion inside the flipflop (see Figure 11.47) Dual-Supply Inside a Logic Block Minimum energy consumption is achieved if all logic paths are critical (have the same delay) Clustered voltage-scaling Each path starts with VDDH and switches to VDDL (gray logic gates) when delay slack is available Level conversion is done in the flipflops at the end of the paths Power and Energy Design Space Constant Throughput/Latency Energy Design Time Variable Throughput/Latency Non-active Modules Logic Design Active Reduced Vdd Run Time DFS, DVS Clock Gating Sizing Multi-Vdd (Dynamic Freq, Voltage Scaling) Sleep Transistors Leakage + Multi-VT Multi-Vdd Variable VT + Variable VT Stack Effect Leakage is a function of the circuit topology and the value of the inputs VT = VT0 + (|-2F + VSB| - |-2F|) where VT0 is the threshold voltage at VSB = 0; VSB is the sourcebulk (substrate) voltage; is the body-effect coefficient A A 0 0 1 1 B Out A VX B B 0 1 0 1 VX VT ln(1+n) 0 VDD-VT 0 ISUB VGS=VBS= -VX VGS=VBS=0 VGS=VBS=0 VSG=VSB=0 Leakage is least when A = B = 0 Leakage reduction due to stacked transistors is called the stack effect Short Channel Factors and Stack Effect In short-channel devices, the subthreshold leakage current depends on VGS,VBS and VDS. The VT of a short-channel device decreases with increasing VDS due to DIBL (drain-induced barrier loading). Typical values for DIBL are 20 to 150mV change in VT per voltage change in VDS so the stack effect is even more significant for short-channel devices. VX reduces the drain-source voltage of the top nfet, increasing its VT and lowering its leakage For our 0.25 micron technology, VX settles to ~100mV in steady state so VBS = -100mV and VDS = VDD -100mV which is 20 times smaller than the leakage of a device with VBS = 0mV and VDS = VDD Reducing the VT increases the subthreshold leakage current (exponentially) 90mV reduction in VT increases leakage by an order of magnitude But, reducing VT decreases gate delay (increases performance) ID (A) Leakage as a Function of Design Time VT VT=0.4V VT=0.1V 0 0.2 0.4 0.6 0.8 1 VGS (V) Determine the critical path(s) at design time and use low VT devices on the transistors on those paths for speed. Use a high VT on the other logic for leakage control. A careful assignment of VT’s can reduce the leakage by as much as 80% Dual-Thresholds Inside a Logic Block Minimum energy consumption is achieved if all logic paths are critical (have the same delay) Use lower threshold on timing-critical paths Assignment can be done on a per gate or transistor basis; no clustering of the logic is needed No level converters are needed Variable VT (ABB) at Run Time VT = VT0 + (|-2F + VSB| - |-2F|) For an n-channel device, the substrate is normally tied to ground (VSB = 0) A negative bias on VSB causes VT to increase Adjusting the substrate bias at run time is called adaptive body-biasing (ABB) Requires a dual well fab process 0.9 0.85 0.8 0.75 0.7 0.65 0.6 0.55 0.5 0.45 0.4 -2.5 -2 -1.5 -1 VSB (V) -0.5 0