Download Chapter 18 Electric Currents

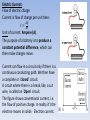
Chapter 18
Electric Currents
Electric Current:
Flow of electric charge
Current is flow of charge per unit time:
∆𝑄
𝐼= .
∆𝑡
Unit of current: Ampere (A).
The purpose of a battery is to produce a
constant potential difference, which can
then make charges move.
Current can flow in a circuit only if there is a
continuous conducting path. We then have
a complete or ‘closed’ circuit.
A circuit where there is a break, like, a cut
wire, is called an ‘Open’ circuit.
The figure shows conventional current, i.e.
the flow of positive charge. In reality it’s the
electron moves in solids- Electron current.
Ohm’s Law : Resistance and Resistors
- Current through a wire is directly proportional to applied
voltage.
𝐼∝𝑉
Removing the sign of proportionality,
𝑉 = 𝐼𝑅
where ‘𝑅’ is called the ‘Resistance’ of the circuit.
It has been also seen that the Resistance of a wire is directly
proportional to the length of the wire and inversely proportional
to the cross sectional area of the wire. Mathematically,
𝑙
𝑅=𝜌
𝑎
Where 𝜌 is called the ‘Resistivity’ of the wire.
The Resistivity depends only the temp of the surrounding.
Temperature Dependence of Resistivity:
𝜌𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0
𝜌0 : Resistivity at some reference Temperature 𝑇0
𝜌𝑇 : Resistivity at temperature T
𝛼: Temperature coefficient of resistivity
Electric Power:
𝐸𝑛𝑒𝑟𝑔𝑦 𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑑 𝑄𝑉
𝑃=
=
= 𝐼𝑉
𝑡𝑖𝑚𝑒
𝑡
Also, 𝑉 = 𝐼𝑅. So,
2
𝑉
𝑃 = 𝐼𝑉 = 𝐼 2 𝑅 =
𝑅
Unit of Power(P): Watt (W).
1W = 1 J/s.
Household Circuits:
- Connected such that each appliance
gets same Voltage (Parallel
connection).
- When a wire carries more that its safe,
the circuit is called overloaded, which
causes heating, and fire. To prevent
this we use circuit breaker or fuses.
- Each wire has a limit up to which it can
hold current (Current Rating), after
which the heat produced at the rate of
I2R is too high for the insulating
material.
Problem 1:
A hair dryer draws 13.5 A when plugged into a 120V line.
a) What is the resistance ?
b) How much charge passes through it in 15 min. (Assume direct
current ).
Solution:
a) Ohm’s Law: V=IR.
So, R = V/I = 120/13.5 = 8.88 Ω
b) Current, I = charge/time = Q/t
So, Charge (Q) =I x t =13.5 X 15 x 60s = 12150C.
Problem 2:
Two aluminum wires have the same resistance. If one has twice
the length of the other, what is the ratio of the diameter of the
longer wire to the shorter wire?
Solution:
𝑙𝑙
For longer wire: 𝑅𝑙 = 𝜌
For shorter wire: 𝑅𝑠 =
𝑎𝑙
𝑙𝑠
𝜌
𝑎𝑠
According to the problem, Rl = Rs
𝑙𝑙
𝑙
So,
= 𝑠
𝑎𝑙
𝑎𝑙
𝑎𝑠
=
𝑙𝑙
𝑙𝑠
=2
𝑎𝑠
or,
𝑑𝑙
𝑑𝑠
= 2
Problem 3:
At $0.095/kWh, what does it cost to leave a 25W porch light on
day and night for a year ?
Solution:
kWh (kilo-Watt hour)is the unit of energy. This is the unit that
your electric company use to charge for your electricity
consumption.
If 1000W power is used in 1 hour, we say the appliance consumed
1kWh of energy.
Thus,
Total energy Spent by the porch light = 25 W x 1 year
= 25 W x 365 x 24 hours = 219000 Watt- hour
= 219kWh.
So, total cost = 219 x$0.095 = $20.8
Problem 4:
A 100 W light bulb has a resistance of about 12 ohm when cold
(200C ) and 140 Ohm when on (hot). Estimate the temperature of
the filament when hot assuming the temperature coefficient of
resistivity α = 0.0045(C0)-1.
Solution:
𝑙
𝜌𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0
Remember: 𝑅 = 𝜌
𝑎
Hence for constant ‘𝑙’ and ‘a’, we can replace 𝜌 by R. Thus,
140 = 12 [1+ 0.0045(T-20)]
So, T = 2390 0C.
Alternating Current (AC):
- Reverses direction many times a
second, and are usually sinusoidal.
All currents supplied to household
are AC all over the world.
The voltage produced by generators
are sinusoidal and can be expressed
as a function of time as:
𝑉 = 𝑉0 𝑠𝑖𝑛2𝜋𝑓𝑡 = 𝑉0 𝑠𝑖𝑛𝜔𝑡
Ohm’s law also holds good for ac.
Hence, above equation can be
written as:
𝐼 = 𝐼0 𝑠𝑖𝑛𝜔𝑡
𝐼0 𝑎𝑛𝑑 𝑉0 : Peak Current and Peak
Voltage.
Over a full cycle, the average current is zero. This would imply the
power is also zero, but this is not the case. The electron is losing
some energy at every instant whether it be moving forward or
backward in a circuit.
At a given time t, the power transformed in the resistance R is:
𝑃 = 𝐼 2 𝑅 = 𝐼02 𝑅𝑠𝑖𝑛2 𝜔𝑡
You can also see from this equation, 𝐼02 is always positive. Also, the
value of sine lies between -1 and 1. But as it is squared, it is also
positive.
Average of 𝑠𝑖𝑛2 𝜔𝑡 = 1/2.
(Refer to your textbook.)
Hence the average power
transformed is ,
1 2
1 𝑉02
𝑃 = 𝐼0 𝑅 =
2
2 𝑅
Since using the average current or voltage values for ac will predict
zero power transformed over a cycle, which is not true, we take
the square of the average of these quantities. This is called the
root mean square (rms) value of current or voltage:
𝐼0
2
𝐼𝑟𝑚𝑠 = 𝐼 =
= 0.707𝐼0
2
𝑉0
2
𝑉𝑟𝑚𝑠 = 𝑉 =
= 0.707𝑉0
2
So, the average power can also be calculated as,
1 2
2
𝑃 = 𝐼𝑟𝑚𝑠 𝑉𝑟𝑚𝑠 = 𝐼0 𝑅 = 𝐼𝑟𝑚𝑠
𝑅
2
2
2
1 𝑉0
𝑉𝑟𝑚𝑠
=
=
2 𝑅
𝑅
This implies that in order to generate same power, the I and V used
is direct current (dc) is replaced by its rms values of I and V in ac. In
USA, the standard line voltabe is 120V-ac, and is the rms value.
Microscopic View of Electric Current
When electric current is
passed through a wire, the
electron attains a steady
velocity, which is called the
drift velocity (vd). As the
electron collide with the
atoms of the wire, it cannot
accelerate further. Let n be
the number of charges per
unit volume. Then,
∆Q = Number of charges x Charge per particle
= (nV)e = (nAvd Δt)(e)
So, magnitude of Current I in the wire:
I = ΔQ/ Δt = neAvd
Problem 5:
Determine the maximum instantaneous power dissipated by a
2.2hp pump connected to a 240 Vrms ac power source, and the
maximum current passing through the pump.
Solution:
1hp = 746 Watt
Prms= Vrms x Irms
Hence, Irms =2.2 x 746/240 V = 6.84 A.
R= Vrms/Irms = 240/6.84 = 35.08 Ohms
Pmax = V2max/R = 2 X 2402/35.08 = 3291 Watt.
Where ‘2’ is because Vmax = 1.414 x Vrms
So, Ipeak = 1.414 x Irms = 9.67 A
Problem 6:
A 0.65mm diameter copper wire carries a tiny dc current of 2.7μA.
Estimate the electron drift velocity.
Solution:
We know I = neAvd. All we need to calculate is ‘n’.
Let us determine n for one mole of Copper as it is the standard unit of
measurement. Hence,
𝑁
𝑁
𝑁
𝑛= =𝑚 = 𝜌
𝑉
𝜌 𝑚
For one mole, 𝑛 =
Hence, 𝑣𝑑 =
𝐼
𝑛𝑒𝐴
𝑁 (1 𝑚𝑜𝑙𝑒)
𝜌
𝑚(1 𝑚𝑜𝑙𝑒)
=
6.023×1023
=
× 8.9 ×
63.5×10−3 𝐾𝑔
= 8.4 × 1028 𝑚−3
2.7 ×10−6
8.4 ×1028 ×1.6×10−19 ×𝜋×
2
0.65×10−3
2
103 𝑘𝑔/𝑚3
= 6 × 10−10 𝑚