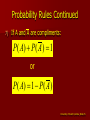Download Probability Class

Probability
A Brief Look
A Few Terms
Probability represents a standardized
measure of chance, and quantifies
uncertainty.
 Let S = sample space which is the set of all
possible outcomes.
 An event is a set of possible outcomes that
is of interest.
 If A is an event outcome, then P(A) is the
probability that event outcome A occurs.

Sample Space, A’s and P(A)’s



What is the chance that it will rain today?
The number of maintenance calls for an
old photocopier is twice that for the new
photocopier. What is the chance that the
next call will be regarding an old
photocopier?
If I pull a card out of a pack of 52 cards, what is
the chance it’s a spade?
Union and Intersection of Events

The intersection of events A and B refers
to the probability that both event A and
event B occur.
P( A  B)
and

The union of events A and B refers to the
probability that event A occurs or event B
occurs or both events, A & B, occur.
P( A  B)
either/or
Mutually Exclusive Events

Mutually exclusive events can not occur
at the same time.
S
Mutually Exclusive Events
S
Not Mutually Exclusive
Events
Roommate profile Distribution
Frequency - Counts
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
Relative Frequency - Probability
Snores
Doesn’t Snore
Parties
0.15
0.10
0.25
Doesn’t Party
0.20
0.55
0.75
0.35
0.65
1.00
University of South Carolina; Slide 6
What is the probability that a
randomly chosen roommate will
snore?
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
What is the probability that a
randomly chosen roommate will
like to party?
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
What is the probability that a
randomly chosen roommate will
snore or like to party?
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
The Union of Two Events

If events A & B intersect, you have
to subtract out the “double count”.
P( A  B)  P( A)  P( B)  P( A  B)

If events A & B do not intersect (are
mutually exclusive), there is no
“double count”.
P( A  B)  P( A)  P( B)
Given that a randomly chosen
roommate snores, what is the
probability that he/she likes to
party?
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
University of South Carolina; Slide 11
Conditional Probability

The conditional probability of B, given
that A has occurred:
P( A  B)
P( B | A) 
P( A)
Given
University of South Carolina; Slide 12
Probability of Intersection

Solving the conditional probability formula
for the probability of the intersection of A
and B:
P( A  B)
P( B | A) 
P( A)
P( A  B)  P( A)  P( B | A)
When P( B | A)  P( B) , we say that
Events B and A are Independent.
The basic idea underlying independence is
that information about event A provides no
new information about event B. So “given
event A has occurred”, doesn’t change our
knowledge about the probability of event B
occurring.
 There
are 10 light bulbs in a bag, 2
are burned out.
 If we randomly choose one and test
it, what is the probability that it is
burned out?
 If we set that bulb aside and
randomly choose a second bulb, what
is the probability that the second bulb
is burned out?
Near Independence

EX: Car company ABC manufactured
2,000,000 cars in 2009; 1,500,000 of
the cars had anti-lock brakes.
– If we randomly choose 1 car, what
is the probability that it will have
anti-lock brakes?
– If we randomly choose another car,
not returning the first, what is the
probability that it will have anti-lock
brakes?
Independence

Sampling with replacement makes
individual selections independent from
one another.

Sampling without replacement from
a very large population makes
individual selection almost independent
from one another
Probability of Intersection

Probability that both events A and B occur:
P( A  B)  P( A)  P( B | A)

If A and B are independent, then the
probability that both occur:
P( A  B)  P( A)  P( B)
Test for Independence


If P( B | A)  P( B) , then A and B are
independent events.
If A and B are not independent events,
they are said to be dependent events.
University of South Carolina; Slide 19
Are snoring or not and partying
or not independent of one
another?
Snores
Doesn’t Snore
Parties
150
100
250
Doesn’t Party
200
550
750
350
650
1000
University of South Carolina; Slide 20
Arrange the counts so that
snoring and partying are
independent of one another.
Snores
Doesn’t Snore
Parties
Doesn’t Party
1000
University of South Carolina; Slide 21
Complementary Events
The complement of an event is every
outcome not included in the event, but still
part of the sample space.
 The complement of event A is denoted A.
 Event A is not event A.

S:
A
A
P( A)  P( A )  1
P( A)  1  P( A )
University of South Carolina; Slide 22
?????????????????
All mutually exclusive events are
complementary.
True
B. False
A.
University of South Carolina; Slide 23
Probability Rules
0 < P(A) < 1
2) Sum of all possible mutually exclusive
outcomes is 1.
3) Probability of A or B:
1)
P( A  B)  P( A)  P( B)  P( A  B)
4)
Probability of A or B when A, B are mutually
exclusive:
P( A  B)  P( A)  P( B)
University of South Carolina; Slide 24
Probability Rules Continued
4)
Probability of B given A:
5)
Probability of A and B:
P( A  B)
P( B | A) 
P( A)
P( A  B)  P( A)  P( B | A)
6)
Probability of A and B when A, B are
independent:
P( A  B)  P( A)  P( B)
University of South Carolina; Slide 25
Probability Rules Continued
7)
If A and A are compliments:
P( A)  P( A )  1
or
P( A)  1  P( A )
University of South Carolina; Slide 26
So Let’s Apply the Rules

We purchase 30% of our parts from
Vendor A. Vendor A’s defective rate is 5%.
What is the probability that a randomly
chosen part is defective and from Vendor
A?
University of South Carolina; Slide 27
????????????

We are manufacturing widgets. 50% are
red, 30% are white and 20% are blue.
What is the probability that a randomly
chosen widget will not be white?
University of South Carolina; Slide 28
????????????

When a computer goes down, there is a
75% chance that it is due to overload and
a 15% chance that it is due to a software
problem. There is an 85% chance that it is
due to an overload or a software problem.
What is the probability that both of these
problems are at fault?
University of South Carolina; Slide 29
????????????

It has been found that 80% of all
accidents at foundries involve human error
and 40% involve equipment malfunction.
35% involve both problems. If an accident
involves an equipment malfunction, what
is the probability that there was also
human error?
University of South Carolina; Slide 30
?????????????????
Four electrical components are connected in
series. The reliability (probability the
component operates) of each component is
0.90. If the components are independent of
one another, what is the probability that the
circuit works when the switch is thrown?
A
B
C
D
University of South Carolina; Slide 31
An automobile manufacturer gives a 5year/75,000-mile warranty on its drive
train. Historically, 7% of the
manufacturer’s automobiles have required
service under this warranty. Consider a
random sample of 15 cars.
 If we assume the cars are independent of
one another, what is the probability that
no cars in the sample require service
under the warranty?
 What is the probability that at least one
car in the sample requires service?

University of South Carolina; Slide 32
Consider the following electrical circuit:
A
0.95
B
0.95
C
0.95
The probability on the components is their
reliability (probability that they will
operate when the switch is thrown).
Components are independent of one
another.
 What is the probability that the circuit will
not operate when the switch is thrown?

University of South Carolina; Slide 33
Consider the electrical circuit below.
Probabilities on the components are
reliabilities and all components are
independent. What is the probability that
the circuit will work when the switch is
thrown?
A
0.90
B
C
0.95
0.90
University of South Carolina; Slide 34
The number of maintenance calls for an
old photocopier is twice that for the new
photocopier.
Outcomes
Old Machine
New Machine
Probability
0.67
0.33
Which of the following series of events would most
cause you to question the validity of the above
probability model?
A.
B.
C.
D.
Two maintenance calls for an old machine followed by a call
for a new machine.
Two maintenance calls for new machines followed by a call
for an old machine.
Three maintenance calls in a row for an old machine.
Three maintenance calls in a row for a new
Universitymachine
of South Carolina; Slide 35
?????

What is the probability that at least 2
people in this class (n=39) have the same
birthday – Month and day?
– Year has 365 days – forget leap year.
– Equally likelihood for each day
University of South Carolina; Slide 36
Multiplication of Choices

If an operation can be performed in n1
ways, and if for each of these a second
operation can be performed in n2 ways,
and for each of the first two a third
operation can be performed in n3 ways,
and so forth, then the sequence of k
operations can be performed in n1 · n2 ·…·
nk ways.
University of South Carolina; Slide 37
Multiplication of Choices

There are 5 processes needed to manufacture
the side panel for a car: clean, press, cut, paint,
polish. Our plant has 6 cleaning stations, 3
pressing stations, 8 cutting stations, 5 painting
stations, and 8 polishing stations.
– How many different “pathways” through the
manufacturing exist?
– What is the number of “pathways” that include a
particular pressing station?
– What is the probability that a panel follows any
particular path?
– What is the probability that a panel goes through
pressing station 1?
Classical Definition of Probability
If an experiment can result in any one
of N different, but equally likely,
outcomes, and if exactly n of these
outcomes corresponds to event A, then
the probability of event A is
n
P( A) 
N
University of South Carolina; Slide 39
Counting

Suppose there are 3 vendors and we want
to choose 2. How many possible
combinations of 2 can be chosen from the
3 vendors?
University of South Carolina; Slide 40
Counting - Combinations

The number of combinations of n distinct
objects taken r at a time is
 n
n!


C


n r
 r  r!(n  r )!
 
“n choose r”
University of South Carolina; Slide 41
Factorial Reminder

n! = n · (n-1) · (n-2) ·…..
– EX: 4! = (4)(3)(2)(1) = 24

1! = 1
0! = 1
5
5!
5 C2  
 2   2!(5  2)!  10
 
University of South Carolina; Slide 42
Counting

9 out of 100 computer chips are defective. We
choose a random sample of n=3.
– How many different samples of 3 are possible?
– How many of the samples of 3 contain exactly 1
defective chip?
– What is the probability of choosing exactly 1 defective
chip in a random sample of 3?
– What is the probability of choosing at least 1
defective chip in a random sample of 3?
University of South Carolina; Slide 43
This class consists of 5 women and 34
men. If we randomly choose 4 people,
what is the probability that there will be
no women chosen?
 What is the probability that there will be
at least 1 woman chosen?

University of South Carolina; Slide 44