Download Geometry Name______________________________ Intro to

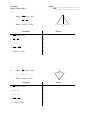
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
For #1-5 evaluate the diagram, mark the necessary information, and support each reason
with a statement.
1.
Given: ZY  WX and ZW  YX
Y
Z
Prove: △WZT ≅ △YXW
X
W
Statements
Reasons
1. ZY  WX and ZW  YX
1.
2. WY  WY
2.
3. △WZT ≅ △YXW
3.
2.
Given: X is the midpoint of AB and CD .
A
C
Prove: ACX  BDX
X
D
Statements
Reasons
1. X is the midpoint of AB and CD .
1.
2. AXC  DXB
2.
3. CX  DX
3.
4. AX  BX
4.
5. △AXC ≅ △BXD
5.
6. ACX  BDX
6.
B
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
3.
Z
Given: ZW bisects ∠XZY
1 2
XZ  YZ
Prove: △XWZ ≅ △YWZ
X
Statements
Reasons
1. ZW bisects ∠XZY
1.
2. XZ  YZ
2.
3. ∠1 = ∠2
3.
4. ZW  ZW
4.
5. △XWZ ≅ △YWZ
5.
4.
Y
W
Given: BD bisects ∠ABC
B
A
∠A = ∠C
Prove: △ABD ≅ △CBD
1 2
D
Statements
Reasons
1. BD bisects ∠ABC
1.
2. ∠A = ∠C
2.
3. ∠1 = ∠2
3.
4. BD  BD
4.
5. △ABD ≅ △CBD
5.
C
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
5. Given: AC || DB
B
D
X is the midpoint of AB
Prove: AXC  BXD
X
Statements
Reasons
1. AC || DB
1.
2. X is the midpoint of AB
2.
3. AX  XB
3.
4. DBX  XAC
4.
5. BDX  XCA
5.
6. AXC  BXD
6.
7. DX  XC
7.
C
A
For #6-10 evaluate the diagram, mark the necessary information, and for each reason give
the appropriate statement.
G
6. Given: HK bisects GKN
G  N
Prove: GKH  NKH
Statements
H
Reasons
1.
1. Given
2.
2. Given
3.
3. Definition of Angle Bisector
4.
4. Reflexive Property (Shared Side)
5.
5. AAS
N
K
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
7. Given: AY  BY
Y
X is the midpoint of AB
Prove: AXY  BXY
Statements
Reasons
1.
1. Given
2.
2. Definition of Midpoint
3.
3. Reflexive (shared side)
4.
4. SSS
5.
5. CPCTC
8.
A
B
X
D
B
Given: X is the midpoint of AB & CD
Prove: AXC  BXD
Statements
X
Reasons
1.
1. Given
2.
2. Definition of midpoint
3.
3. Definition of midpoint
4.
4. Vertical angles are congruent
5.
5. SAS
A
C
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
R
S
9. Given: ∠S = 90˚and ∠T = 90˚
V is the midpoint of ST
Prove: ∆RSV  ∆UTV
V
Statements
Reasons
U
T
1.
1. Given
2.
2. Definition of midpoint
3.
3. Vertical angles are congruent
4.
4. All right angles are congruent
5.
5. ASA
A
10. Given: AB CD
C
X is the midpoint of AD
X
Prove: BX  XC
B
Statements
D
Reasons
1.
1. Given
2.
2. Definition of Midpoint
3.
3. Vertical angles are congruent
4.
4. Alternate interior angles are congruent when
lines are parallel
5.
5. ASA
6.
6. CPCTC
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
For #11-15 fill in the missing pieces of either the reasons or statements columns.
R
T
11. Given: E is the midpoint of TP and MR
E
Prove: TM  RP
P
M
Statements
Reasons
1.
1. Given
2. TE  EP
2.
3. ME  ER
3.
4.
4. Vertical angles are congruent
5.
5. SAS
6. TM  RP
6.
12.
Q
Given: PR bisects QPS
PR bisects QRS
P
R
Prove: PQR  PSR
Statements
S
Reasons
1.
1. Given
2. QRP  SRP
2.
3.
3. Definition of Angle Bisector
4. PR  PR
4.
5.
5. ASA
D
C
Geometry
Intro to Proofs Day 3
Name______________________________
Date__________________________
13. Given: AB || DC
AB  DC
Prove: CDA  ABC
A
Statements
B
Reasons
1. AB || DC and AB  DC
1.
2.
2. Reflexive (shared side)
3. DCA  BCA
3.
4.
4. SAS
5.
5. CPCTC
T
R
14. Given: TM || PR
TM  PR
E
Prove: TEM  PER
P
M
Statements
Reasons
1. TM  PR and TM || PR
1. Given
2.
2. Vertical angles are congruent
3. MTE  RPE
3.
4.
4. AAS
Geometry
Intro to Proofs Day 3
15. Given:
,
Name______________________________
Date__________________________
,
,
,
Prove:
Statements
1. Given
1.
2.
Reasons
,
2. Given
3.
3.
4.
4. All right angles are congruent.
5.
5. Given
6.
6.
7.
7. Given
8.
8.
9.
9.