Download Similarity in Right Triangles

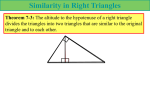
Similarity in Right Triangles
Lesson 8.1
Pre-AP Geometry
Lesson Focus
Right triangles have many interesting properties. This lesson
begins with a study of the properties of right triangles.
Algebraic skills with radicals are reviewed and are used
throughout the chapter.
Simplifying Radicals
Product Rule for Radicals
For any nonnegative numbers a and b and any natural
number index n,
n
a  n b  n ab
Quotient Rule for Radicals
For any natural number index n and any real numbers a
and b (b  0) where n a and n b are real numbers,
n
a na
 n
b
b
Simplifying Radicals
Radical expressions are written in simplest terms when:
• The index is as small as possible
• The radicand contains no factor (other than 1) which is the nth
power of an integer or polynomial.
• The radicand contains no fractions.
• No radicals appear in the denominator.
Simplifying Radicals
Example 1:
75
Example 2:
2
5
Example 3: 2 48
Example 4:
16  4
Geometric Mean
a x
 , then x is the
If a, b, and x are positive numbers with
x
b
geometric mean between a and b.
This implies that x  ab .
Geometric Mean
Example 5: Find the geometric mean of 4 and 9.
Example 6: Find the geometric mean of 3 and 48.
Important
To be successful in this chapter, you should spend the time to
memorize the following theorem and corollaries.
It is very important to your success in this chapter to
remember these rules and know how use them.
Right Triangle Similarity Theorem
If the altitude is drawn to the hypotenuse of a right triangle,
then the two triangles formed are similar to the original
triangle and to each other.
ACB  ADC  CDB
A
C
D
B
Corollary 1
When the altitude is drawn to the hypotenuse of a right
triangle, the length of the altitude is the geometric mean
between the segments of the hypotenuse.
C
AD CD

CD DB
A
D
B
Corollary 2
When the altitude is drawn to the hypotenuse of a right
triangle, each leg is the geometric mean between the
hypotenuse and the segment of the hypotenuse that is
adjacent to that leg.
C
AB AC

AC AD
AB BC

BC BD
A
D
B
Similarity in Right Triangles
C
Example 7: If BD = 16 and AD = 9,
find CD, AB, CB, and AC.
A
D
B
Similarity in Right Triangles
C
Example 8: If BD = 4 and CD = 2,
find AD, AB, CB, and AC.
A
D
B
Written Exercises
Problem Set 8.1A, p.288: # 2 - 38 (even)
Written Exercises
Problem Set 8.1B, Handout 8-1