Download Geometry Name 1.3 Angles and Their Measures Date

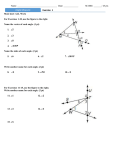
Geometry
1.3 Angles and Their Measures
Name ______________________________
Date ________________ Period ______
Objectives
Name and classify angles.
Measure and construct angles and angle bisectors.
angle – a figure formed by two ______, or sides, with a common _____________ called the vertex (plural:
vertices).
Angle Name: ________, ________, ________, or _______
You cannot name an ______ just by its ______ if the point is the vertex of more than ____ _______. In this
case, you must use all _____ _______ to name the angle, and the _______ point is always the vertex.
Example 1
Write the different ways you can name the angles in the diagram.
Example 2
Classify each angle as acute, right, or obtuse.
A. XTS
B. WTU
C. XTU
Example 3
Find the measure of each angle.
Example 4
Use a protractor to draw an angle with a measure of 165°.
Example 5
Find the measure of each angle. Then classify each as acute, right, or obtuse.
A. YXW
B. ZXW
C. WXV
Example 6
Find the measure of each angle. Then classify each as acute, right, or obtuse.
A. AOB
B. BOC
C. COD
D. DOB
Congruent angles are angles that have the same ___________.
In the diagram, mABC = mDEF,
so ABC  DEF.
Example 7
Example 8
mDEG = 115°, and mDEF = 48°. Find mFEG.
K is in the interior of LMN, mLMK =52°, and
mKMN = 12°. Draw the picture. Find mLMN.
An angle bisector is a _____ that divides an angle into ____ _________ ______.
⃗⃗⃗⃗ bisects LJM;
JK
thus LJK  KJM.
Example 9
⃗⃗⃗⃗⃗⃗ bisects JKL, mJKM = (4x + 6)°, and
KM
mMKL = (7x – 12)°. Find mJKM.
Example 10
⃗⃗⃗⃗ bisects LJM, mLJK = (-10x + 3)°, and
JK
mKJM = (–x + 21)°. Find mLJM.
Example 11
⃗⃗⃗⃗⃗
QS bisects PQR, mPQS = (5y – 1)°, and
mPQR = (8y + 12)°. Find mPQS.
Example 12
1
⃗⃗⃗⃗⃗
BD bisects ABC, mABD = (2y + 10) °, and
mDBC = (y + 4)°. Find mABC.