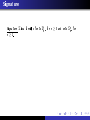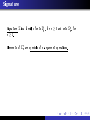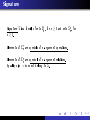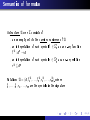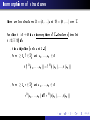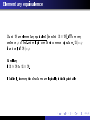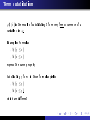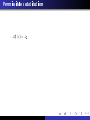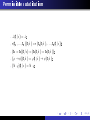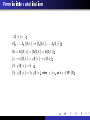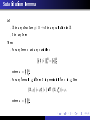Download First-order logic syntax and semantics

First-order logic syntax and semantics
First-order logic is also known as predicate logic and
predicate calculus
Signature
Signature
n ≥ 1.
Σ
is a family of sets
ΣFn ,
for
n ≥ 0 and sets ΣRn , for
Signature
Signature
n ≥ 1.
Σ
Elements of
is a family of sets
ΣFn
are symbols of
ΣFn ,
for
n ≥ 0 and sets ΣRn , for
n-argument operations.
Signature
Signature
n ≥ 1.
Σ
is a family of sets
ΣFn
ΣFn ,
for
n ≥ 0 and sets ΣRn , for
are symbols of
n-argument operations.
Elements of
are symbols of
n-argument relations.
Equality
does not belong to
Elements of
ΣR
n
sign =
Σ.
Signature
Signature
n ≥ 1.
Σ
is a family of sets
ΣFn
ΣFn ,
for
n ≥ 0 and sets ΣRn , for
are symbols of
n-argument operations.
Elements of
are symbols of
n-argument relations.
Equality
does not belong to
Elements of
ΣR
n
sign =
Σ.
If the signature is nite and the arities are known, it is often
presented as a sequence of symbols, e.g.,
+, ·, 0, 1
Variables and terms
We x a countably innite set
X
of individual variables.
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Σ
and variable set
X:
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Individual variables are terms
Σ
and variable set
X:
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Individual variables are terms
Σ
and variable set
X:
n ≥ 0 and every symbol f ∈ ΣFn , if t1 , . . . , tn are
terms, then f (t1 , . . . , tn ) is also a term
For every
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Individual variables are terms
Σ
and variable set
X:
n ≥ 0 and every symbol f ∈ ΣFn , if t1 , . . . , tn are
terms, then f (t1 , . . . , tn ) is also a term
The set FV (t ) of variables occurring in t :
For every
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Individual variables are terms
Σ
and variable set
X:
n ≥ 0 and every symbol f ∈ ΣFn , if t1 , . . . , tn are
terms, then f (t1 , . . . , tn ) is also a term
The set FV (t ) of variables occurring in t :
FV (x ) = {x }.
For every
Variables and terms
We x a countably innite set
The set of terms
TΣ (X )
X
of individual variables.
over signature
Individual variables are terms
Σ
and variable set
X:
n ≥ 0 and every symbol f ∈ ΣFn , if t1 , . . . , tn are
terms, then f (t1 , . . . , tn ) is also a term
The set FV (t ) of variables occurring in t :
FV (x ) = {x }.
S
FV (f (t1 , . . . , tn )) = ni=1 FV (ti ).
For every
Atomic formulas
The set of atomic formulas over
Σ
and
X:
Atomic formulas
The set of atomic formulas over
Falsity
⊥
Σ
is an atomic formula
and
X:
Atomic formulas
The set of atomic formulas over
Falsity
⊥
Σ
is an atomic formula
and
X:
n ≥ 1, each symbol r ∈ ΣRn , and each n terms
t1 , . . . , tn ∈ TΣ (X ), the expression r (t1 , . . . , tn ) is an atomic
For each
formula
Atomic formulas
The set of atomic formulas over
Falsity
⊥
Σ
and
X:
is an atomic formula
n ≥ 1, each symbol r ∈ ΣRn , and each n terms
t1 , . . . , tn ∈ TΣ (X ), the expression r (t1 , . . . , tn ) is an atomic
For each
formula
For each two terms
formula
t1 , t2 , the expression (t1 = t2 ) is an atomic
Formulas
The set of formulas over
Σ
and
X:
Formulas
The set of formulas over
Σ
and
X:
Each atomic formula is a formula
Formulas
The set of formulas over
Σ
and
X:
Each atomic formula is a formula
If
ϕ, ψ
are formulas, then
(ϕ → ψ)
is a formula
Formulas
The set of formulas over
Σ
and
X:
Each atomic formula is a formula
If
ϕ, ψ
If
ϕ
are formulas, then
is a formula and
formula
(ϕ → ψ)
x ∈X
is a formula
is a variable, then
(∀x ϕ)
is a
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
Free variables of a formula
The set of free variables
FV (⊥) = ∅;
FV (ϕ) of a formula ϕ:
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
FV (⊥) = ∅;
S
FV (r (t1 , . . . , tn )) = ni=1 FV (ti );
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
FV (⊥) = ∅;
S
FV (r (t1 , . . . , tn )) = ni=1 FV (ti );
FV (t1 = t2 ) = FV (t1 ) ∪ FV (t2 );
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
FV (⊥) = ∅;
S
FV (r (t1 , . . . , tn )) = ni=1 FV (ti );
FV (t1 = t2 ) = FV (t1 ) ∪ FV (t2 );
FV (ϕ → ψ) = FV (ϕ) ∪ FV (ψ);
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
FV (⊥) = ∅;
S
FV (r (t1 , . . . , tn )) = ni=1 FV (ti );
FV (t1 = t2 ) = FV (t1 ) ∪ FV (t2 );
FV (ϕ → ψ) = FV (ϕ) ∪ FV (ψ);
FV (∀x ϕ) = FV (ϕ) − {x }.
Free variables of a formula
The set of free variables
FV (ϕ) of a formula ϕ:
FV (⊥) = ∅;
S
FV (r (t1 , . . . , tn )) = ni=1 FV (ti );
FV (t1 = t2 ) = FV (t1 ) ∪ FV (t2 );
FV (ϕ → ψ) = FV (ϕ) ∪ FV (ψ);
FV (∀x ϕ) = FV (ϕ) − {x }.
A formula without quantiers is an open formula.
A formula without free variables is a sentence, or a closed formula.
Syntax abbreviations
Additional propositional connectives are abbreviations:
(¬ϕ)
ϕ→⊥
for
(ϕ ∨ ψ)
for
((¬ϕ) → ψ)
(ϕ ∧ ψ)
for
(¬((¬ϕ) ∨ (¬ψ)))
(ϕ ↔ ψ)
for
((ϕ → ψ) ∧ (ψ → ϕ))
The existential quantier is an abbreviation, too:
(∃x ϕ)
means
(¬(∀x ¬ϕ)).
Free vs. bound occurrences of a variable
Each variable occurrence in an atomic formula is a free one
Free vs. bound occurrences of a variable
Each variable occurrence in an atomic formula is a free one
Free (bound) occurrences in
formula
ϕ → ψ.
ϕ
and
ψ
remain free (bound) in the
Free vs. bound occurrences of a variable
Each variable occurrence in an atomic formula is a free one
Free (bound) occurrences in
formula
ϕ
and
ψ
remain free (bound) in the
ϕ → ψ.
Free occurrences of
x
in
ϕ
become bound in
∀x ϕ.
Occurrences of other variables in this formula do not change their
status
Free vs. bound occurrences of a variable
Each variable occurrence in an atomic formula is a free one
Free (bound) occurrences in
formula
ϕ
and
ψ
remain free (bound) in the
ϕ → ψ.
Free occurrences of
x
in
ϕ
become bound in
∀x ϕ.
Occurrences of other variables in this formula do not change their
status
The distinction between free and bound variables resembles the
distinction between local and global variables in a procedure
Semantics of formulas
A structure
A
over
Σ
consists of
Semantics of formulas
A structure
a
A
over
Σ
consists of
nonempty set A:
the carrier or universe of
A
Semantics of formulas
A structure
a
A
over
Σ
consists of
nonempty set A:
the carrier or universe of
an interpretation of each symbol
f A : An → A
f
∈ ΣFn
A
as an
n-ary function
Semantics of formulas
A structure
a
A
over
Σ
consists of
nonempty set A:
the carrier or universe of
A
an interpretation of each symbol
f
∈ ΣFn
as an
n-ary function
an interpretation of each symbol
r ∈ ΣRn
as an
n-ary relation
f A : An → A
r
A
⊆ An
Semantics of formulas
A structure
a
A
over
Σ
consists of
nonempty set A:
the carrier or universe of
A
an interpretation of each symbol
f
∈ ΣFn
as an
n-ary function
an interpretation of each symbol
r ∈ ΣRn
as an
n-ary relation
f A : An → A
r
A
⊆ An
A i,
A = hA, f1A , . . . , fnA , r1A , . . . , rm
f1 , . . . , fn , r1 , . . . , rm are the symbols in the
Notation:
where
signature
Valuation
A valuation in a
Σ-structure A
is a function
%:X →A
Valuation
A valuation in a
is a function
%:X →A
x ∈ X and an element
a
valuation %x : X → A:
(
%(y ) y 6= x
a
%x (y ) =
For a valuation
a modied
Σ-structure A
%,
a variable
a
otherwise
a ∈ A we dene
Values of terms
The value of a term
%
is denoted
[[t
]]A
% or
t ∈ TΣ (X ) in a Σ-structure A under valuation
[[t ]]% .
Values of terms
The value of a term
%
is denoted
[[t
]]A
% or
[[x ]]A
% = %(x ).
t ∈ TΣ (X ) in a Σ-structure A under valuation
[[t ]]% .
Values of terms
The value of a term
%
is denoted
[[t
]]A
% or
[[x ]]A
% = %(x ).
t ∈ TΣ (X ) in a Σ-structure A under valuation
[[t ]]% .
A
A
A
[[f (t1 , . . . , tn )]]A
% = f ([[t1 ]]% , . . . , [[tn ]]% ).
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
(A, %) |= ⊥
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
does not hold
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
(A, %) |= ⊥
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
does not hold
n ≥ 1, r ∈ ΣRn and terms t1 , . . . , tn
A
A
(A, %) |= r (t1 , . . . , tn ) i h[[t1 ]]A
% , . . . [[tn ]]% i ∈ r .
For
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
(A, %) |= ⊥
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
does not hold
n ≥ 1, r ∈ ΣRn and terms t1 , . . . , tn
A
A
(A, %) |= r (t1 , . . . , tn ) i h[[t1 ]]A
% , . . . [[tn ]]% i ∈ r .
A
(A, %) |= t1 = t2 , i [[t1 ]]A
% = [[t2 ]]% .
For
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
(A, %) |= ⊥
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
does not hold
n ≥ 1, r ∈ ΣRn and terms t1 , . . . , tn
A
A
(A, %) |= r (t1 , . . . , tn ) i h[[t1 ]]A
% , . . . [[tn ]]% i ∈ r .
A
(A, %) |= t1 = t2 , i [[t1 ]]A
% = [[t2 ]]% .
For
(A, %) |= (ϕ → ψ),
holds
if
(A, %) |= ϕ
does not hold or
(A, %) |= ψ
Formula satisfaction
(A, %) |= ϕ
is read:
The formula
valuation
ϕ
is satised in the structure
A
under the
%.
The formula
The formula
(A, %) |= ⊥
ϕ is true in the structure A under the valuation %.
ϕ holds in the structure A under the valuation %.
does not hold
n ≥ 1, r ∈ ΣRn and terms t1 , . . . , tn
A
A
(A, %) |= r (t1 , . . . , tn ) i h[[t1 ]]A
% , . . . [[tn ]]% i ∈ r .
A
(A, %) |= t1 = t2 , i [[t1 ]]A
% = [[t2 ]]% .
For
(A, %) |= (ϕ → ψ),
if
(A, %) |= ϕ
holds
(A, %) |= (∀x ϕ)
i for every
does not hold or
(A, %) |= ψ
a ∈ A holds (A, %ax ) |= ϕ.
Satisfaction does not depend on non-free variables
Fact
For any
Σ-structure A
and any formula
ϕ,
assign equal values to all free variables od
(A, %) |= ϕ
i
if valuations
ϕ,
then
(A, %0 ) |= ϕ.
%
and
%0
Satisfaction does not depend on non-free variables
Fact
For any
Σ-structure A
and any formula
ϕ,
assign equal values to all free variables od
(A, %) |= ϕ
i
if valuations
ϕ,
%
and
%0
then
(A, %0 ) |= ϕ.
Hence simplied notation: (A, x : a, y : b) |= ϕ instead of
(A, %) |= ϕ,
when
free variables in
If
ϕ
%(x ) = a
and
%(y ) = b,
and there are no other
ϕ
is a sentence, then the valuation can be disregarded.
Satisfaction does not depend on non-free variables
Fact
For any
Σ-structure A
and any formula
ϕ,
assign equal values to all free variables od
(A, %) |= ϕ
i
if valuations
ϕ,
%
and
%0
then
(A, %0 ) |= ϕ.
Hence simplied notation: (A, x : a, y : b) |= ϕ instead of
(A, %) |= ϕ,
when
free variables in
If
ϕ
%(x ) = a
and
%(y ) = b,
and there are no other
ϕ
is a sentence, then the valuation can be disregarded.
Hence notation
A |= ϕ
Isomorphism of structures
Given are two structures
A = hA, . . .i
and
B = hB , . . .i
over
Σ
Isomorphism of structures
Given are two structures
h:A→B
h:A∼
= B) if:
Function
A = hA, . . .i
and
is an isomorphism of
B = hB , . . .i
Σ-structures
over
Σ
(denoted
Isomorphism of structures
Given are two structures
A = hA, . . .i
and
B = hB , . . .i
over
Σ
h : A → B is an isomorphism of Σ-structures (denoted
h:A∼
= B) if:
h is a bijection (onto and 1-1)
Function
Isomorphism of structures
Given are two structures
A = hA, . . .i
and
B = hB , . . .i
over
Σ
h : A → B is an isomorphism of Σ-structures (denoted
h:A∼
= B) if:
h is a bijection (onto and 1-1)
F
For n ≥ 0, f ∈ Σn and a1 , . . . , an ∈ A
Function
h(f A (a1 , . . . , an )) = f B (h(a1 ), . . . , h(an ))
Isomorphism of structures
Given are two structures
A = hA, . . .i
and
B = hB , . . .i
over
Σ
h : A → B is an isomorphism of Σ-structures (denoted
h:A∼
= B) if:
h is a bijection (onto and 1-1)
F
For n ≥ 0, f ∈ Σn and a1 , . . . , an ∈ A
Function
h(f A (a1 , . . . , an )) = f B (h(a1 ), . . . , h(an ))
For
n ≥ 1, r ∈ ΣRn
and
a1 , . . . , an ∈ A
r A (a1 , . . . , an )
i
r B (h(a1 ), . . . , h(an ))
Properties of isomorphisms
Composition of two isomorphisms is an isomorphism
Properties of isomorphisms
Composition of two isomorphisms is an isomorphism
The reverse function of an isomorphism is an isomorphism
Properties of isomorphisms
Composition of two isomorphisms is an isomorphism
The reverse function of an isomorphism is an isomorphism
Identity
idA : A → A
is an isomorphism
idA : A ∼
=A
Isomorphic structures
A onto B
A∼
=B
If there exists an isomorphism from
are said to be isomorphic, denoted
then these structures
Isomorphic structures
A onto B
A∼
=B
If there exists an isomorphism from
are said to be isomorphic, denoted
The relation of isomorphism is
transitive
then these structures
Isomorphic structures
A onto B
A∼
=B
If there exists an isomorphism from
are said to be isomorphic, denoted
The relation of isomorphism is
transitive
symmetrical
then these structures
Isomorphic structures
A onto B
A∼
=B
If there exists an isomorphism from
are said to be isomorphic, denoted
The relation of isomorphism is
transitive
symmetrical
reexive
then these structures
Isomorphisms and logic
Theorem
If
h:A∼
= B then for every formula ϕ
(A, %) |= ϕ
i
(B, h ◦ %) |= ϕ
Isomorphisms and logic
Theorem
If
h:A∼
= B then for every formula ϕ
(A, %) |= ϕ
If
i
(B, h ◦ %) |= ϕ
x1 , . . . , xn are the free variables of ϕ, then
(A, x1 : a1 , . . . , xn : an ) |= ϕ
i
(B, x1 : h(a1 ), . . . , xn : h(an )) |= ϕ
Isomorphisms and logic cntd.
Theorem
If
A∼
=B
then for every sentence
A |= ϕ
ϕ
i
B |= ϕ
Elementary equivalence
A
and
B
sentence
are elementary equivalent (denoted
ϕ
A ≡ B),
i for every
of rst-order logic over their common signature,
if and only if
B |= ϕ
A |= ϕ
Elementary equivalence
A
and
B
sentence
are elementary equivalent (denoted
ϕ
B |= ϕ
Corollary
A∼
=B
i for every
of rst-order logic over their common signature,
if and only if
If
A ≡ B),
to
A ≡ B.
A |= ϕ
Elementary equivalence
A
and
B
sentence
are elementary equivalent (denoted
ϕ
A ≡ B),
i for every
of rst-order logic over their common signature,
if and only if
A |= ϕ
B |= ϕ
Corollary
If
A∼
=B
to
A ≡ B.
Intuitively, isomorphic structures are logically indistinguishable
Validity and satisability of formulas
A formula
such that
ϕ is satisable
(A, %) |= ϕ.
in
A,
if there exists a valuation
%
in
A
Validity and satisability of formulas
A formula
such that
A formula
ϕ is satisable
(A, %) |= ϕ.
ϕ
is satisable
in
A,
if there exists a valuation
is satisable, if there exists a structure
A,
%
in
A
in which
ϕ
Validity and satisability of formulas
A formula
such that
A formula
ϕ is satisable
(A, %) |= ϕ.
ϕ
in
A,
if there exists a valuation
is satisable, if there exists a structure
A,
%
in
in which
is satisable
ϕ
is true (satised, valid) in
valuation
%
in
A
A,
if
(A, %) |= ϕ
A
holds for every
ϕ
Validity and satisability of sentences
A sentence
is valid
ϕ
is satisable if there exists a structure
A,
in which
ϕ
Validity and satisability of sentences
A sentence
ϕ
is satisable if there exists a structure
is valid
A
is then said to be a model of
ϕ
(denoted
A |= ϕ)
A,
in which
ϕ
Validity and satisability of sentences
A sentence
ϕ
is satisable if there exists a structure
A,
in which
ϕ
is valid
A
is then said to be a model of
ϕ
Σ-structure A is a model of a set
A |= ϕ holds for every ϕ ∈ Γ.
if
(denoted
A |= ϕ)
of sentences
Γ
(denoted
A |= Γ),
Validity and satisability of sentences
A sentence
ϕ
is satisable if there exists a structure
A,
in which
ϕ
is valid
A
is then said to be a model of
ϕ
Σ-structure A is a model of a set
A |= ϕ holds for every ϕ ∈ Γ.
(denoted
A |= ϕ)
of sentences
Γ
(denoted
A |= Γ),
if
Sentence
ϕ
Σ-structure
is a tautology (denoted
|= ϕ),
if it is valid in every
The rst proof: theorem
If
h:A∼
= B then for every formula ϕ
(A, %) |= ϕ
i
(B, h ◦ %) |= ϕ
The rst proof: Lemma
If
h:A∼
= B then for every term t
h([[t ]]A% ) = [[t ]]Bh◦%
Induction:
The rst proof: Lemma
If
h:A∼
= B then for every term t
h([[t ]]A% ) = [[t ]]Bh◦%
Induction:
If
t
is
x , then the thesis h(%(x )) = (h ◦ %)(x ) holds
The rst proof: Lemma
If
h:A∼
= B then for every term t
h([[t ]]A% ) = [[t ]]Bh◦%
Induction:
x , then the thesis h(%(x )) = (h ◦ %)(x ) holds
If t to f (t1 , . . . , tn ) to
If
t
is
h([[f (t1 , . . . , tn )]]A% = h(f A ([[t1 ]]A% , . . . , [[tn ]]A% ))
A
= f B (h([[t1 ]]A
% ), . . . , h([[tn ]]% ))
B
= f B ([[t1 ]]B
h◦% , . . . , [[tn ]]h◦% )
= [[f (t1 , . . . , tn )]]B
h◦%
The rst proof: atomic formulas
The rst proof: atomic formulas
(A, %) 6|= ⊥
and
(B, h ◦ %) 6|= ⊥
The rst proof: atomic formulas
(A, %) 6|= ⊥
and
(B, h ◦ %) 6|= ⊥
(A, %) |= r (t1 , . . . , tn )
i
i
i
i
A
A
h[[t1 ]]A
% , . . . , [[tn ]]% i ∈ r
A
B
hh([[t1 ]]A
% ), . . . , h([[tn ]]% )i ∈ r
B
B
h[[t1 ]]B
h◦% , . . . , [[tn ]]h◦% i ∈ r
(B, h ◦ %) |= r (t1 , . . . , tn )
The rst proof: atomic formulas
(A, %) 6|= ⊥
and
(B, h ◦ %) 6|= ⊥
(A, %) |= r (t1 , . . . , tn )
i
i
i
i
(A, %) |= t1 = t2
A
A
h[[t1 ]]A
% , . . . , [[tn ]]% i ∈ r
A
B
hh([[t1 ]]A
% ), . . . , h([[tn ]]% )i ∈ r
B
B
h[[t1 ]]B
h◦% , . . . , [[tn ]]h◦% i ∈ r
(B, h ◦ %) |= r (t1 , . . . , tn )
i
A
[[t1 ]]A
% = [[t2 ]]%
h([[t1 ]]A% ) = h([[t2 ]]A% )
B
B
i [[t1 ]]h◦% = [[t2 ]]h◦%
i (B, h ◦ %) |= t1 = t2
i
The rst proof: compound formulas
The rst proof: compound formulas
(A, %) |= (ϕ → ψ)
i
(A, %) 6|= ϕ
i
(B, h ◦ %) 6|= ϕ
i
or
(A, %) |= ψ
or
(B, h ◦ %) |= ψ
(B, h ◦ %) |= (ϕ → ψ)
The rst proof: compound formulas
(A, %) |= (ϕ → ψ)
i
(A, %) 6|= ϕ
i
(B, h ◦ %) 6|= ϕ
i
(A, %) |= (∀x ϕ)
or
(A, %) |= ψ
or
(B, h ◦ %) |= ψ
(B, h ◦ %) |= (ϕ → ψ)
a ∈ A holds (A, %ax ) |= ϕ
a
i for all a ∈ A holds (B, h ◦ (%x )) |= ϕ
h(a)
i for all h (a) ∈ B holds (B, (h ◦ %)x
) |= ϕ
b
i for all b ∈ B holds (B, (h ◦ %)x ) |= ϕ
i (B, h ◦ %) |= (∀x ϕ)
i for all
Term substitution
ϕ(t /x )
variable
is the result of substituting
x
in
ϕ.
t
for every free occurrence of a
Term substitution
ϕ(t /x )
variable
is the result of substituting
x
Example:
in
ϕ.
Formulas
∀y (y ≤ x )
∀z (z ≤ x )
express the same property
t
for every free occurrence of a
Term substitution
ϕ(t /x )
variable
is the result of substituting
x
Example:
in
t
for every free occurrence of a
ϕ.
Formulas
∀y (y ≤ x )
∀z (z ≤ x )
express the same property
y for x
∀y (y ≤ y )
∀z (z ≤ y ).
Substituting
which are dierent
in those formulas yields
Permissible substitution
⊥(t /x ) = ⊥;
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
(t1 = t2 )(t /x ) = (t1 (t /x ) = t2 (t /x ));
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
(t1 = t2 )(t /x ) = (t1 (t /x ) = t2 (t /x ));
(ϕ → ψ)(t /x ) = ϕ(t /x ) → ψ(t /x );
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
(t1 = t2 )(t /x ) = (t1 (t /x ) = t2 (t /x ));
(ϕ → ψ)(t /x ) = ϕ(t /x ) → ψ(t /x );
(∀x ϕ)(t /x ) = ∀x ϕ;
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
(t1 = t2 )(t /x ) = (t1 (t /x ) = t2 (t /x ));
(ϕ → ψ)(t /x ) = ϕ(t /x ) → ψ(t /x );
(∀x ϕ)(t /x ) = ∀x ϕ;
(∀y ϕ)(t /x ) = ∀y ϕ(t /x ), when y 6= x , and y 6∈ FV (t );
Permissible substitution
⊥(t /x ) = ⊥;
r (t1 , . . . , tn )(t /x ) = r (t1 (t /x ), . . . , tn (t /x ));
(t1 = t2 )(t /x ) = (t1 (t /x ) = t2 (t /x ));
(ϕ → ψ)(t /x ) = ϕ(t /x ) → ψ(t /x );
(∀x ϕ)(t /x ) = ∀x ϕ;
(∀y ϕ)(t /x ) = ∀y ϕ(t /x ), when y 6= x , and y 6∈ FV (t );
otherwise the substitution is not permissible
Substitution lemma
Let
A
t
be any structure
be any term
%:X →A
be any valuation in
A
Substitution lemma
Let
A
t
be any structure
%:X →A
be any valuation in
be any term
Then:
For any term
s
and any variable
x
A
[[s (t /x )]]A
% = [[s ]]%ax
where
a = [[t ]]A% .
A
Substitution lemma
Let
A
t
be any structure
%:X →A
be any valuation in
A
be any term
Then:
For any term
s
and any variable
x
A
[[s (t /x )]]A
% = [[s ]]%ax
where
a = [[t ]]A% .
For any formula
ϕ,
if term
t
is permissible for
(A, %) |= ϕ(t /x )
where
a = [[t ]]A% .
i
x
(A, %ax ) |= ϕ,
in
ϕ,
then