Download lecture 5 - darroesengineering

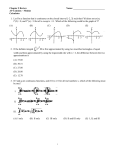
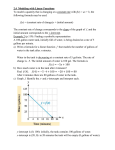
LECTURE 5
BOUYANCY AND STABILITY
3.7 BOUYANCY AND STABILITY
If an object is immersed in or floating on the surface of a liquid, the force acting on it due to
liquid pressure is termed buoyancy. Consider the object shown in figure below, immerse in
static liquid.
po 
dA
h1
F1
h
h2
Liquid, density = ρ
d
z
F2
Fig. Immersed body in static fluid
The vertical force on the body due to hydrostatic pressure may be found most easily by
considering cylindrical volume elements that shown in figure above. For a static fluid
dp
 g
dh
dp  gdh

p
pO
dp    gdh
Integrating for constant ρ gives
p  po  gh
The net vertical force on the element is therefore
Fz  F2  F1   po  gh2 dA   po  gh1 dA  g h2  h1 dA
But h2  h1 dA  d , the volume of element. Thus
Fz   dFz  gd  g

Since floating bodies are in equilibrium under body and buoyancy forces, the location of the
line of action of the buoyancy force determines stability, as shown in figure below:
CG


F buoyancy
F gravity

CG


F buoyancy
F gravity
(a) Stable
(b) Unstable
Example 3.8
King Heiro ordered a new crown to be made from pure gold. When he received the crown, he
suspected that other metals had been used in its construction. Archimedes discovered that the
crown required a force of 4.7 lbf to suspend it when immerse water, and that it displaced 18.9
in3. of water. He concluded that the crown could not be pure gold. Do you agree?
GIVEN:
Crown volume,  = 18.9 in3.
Force water to suspend in water, Fact = 4.7 lbf

F net


F buoyancy
z

F gravity
FIND:
Average density of material in crown.
SOLUTION:


Apply F  m a to immersed crown.

 = 18.9 in3




F  m a
Basic equations:

F buoyancy   H 2O g k

Assume: a  0 for crown. Then


F  F
F
or
act

act


 F gravity  F buoyancy  m a  0


 Fgravity   H 2O g k  0
But Fgravity   c g , where  c is the density of the crown material, so
Fgravity  Fnet   H 2O g   c g
and
c   H O
2
 c  15.3
Fnet 1.94 slug
1
sec 2
slug  ft 1728 in 3 .


 4.7 lbf 



g
ft 3
18.9 in 3 . 32.2 ft lbf  sec
ft 3
slug
ft 3
This is about thesame densityas steel.Sincegoldis heavier than steel, 


the crown couldnot be puregold.

3.7 FLUIDS IN RIGID-BODY MOTION




d F    grad p   g d



or

dF
  grad p   g
d
(3.22)
Newton’s second law was written



d F  a dm  a  d

or

dF
a
d
Substituting from Eq. 3.22, we obtain


 grad p   g   a
The physical significance of each term in this equation is reviewed as follows:
 grad p

+
g

=
a
 accelerati on
 mass per

pressure force per
 + body force per
x
=


 
unit
volum
e
 of fluid particle 
 unit volum e at a point   unit volum e at a point  
This vector equation consists of three component equations that must be satisfied
individually. In rectangular coordinates the component equations are

p
 g x  a x
x
x direction

p
 g y  a y
y
y direction

p
 g z  a z
z
z direction
(3.20)
Example 3.9
As a result of a promotion, you are transferred from your present location. You must
transport a fish tank in the back of your station wagon. The tank is 12 in. x 24 in. x 12 in.
How much water should you leave in the tank to be reasonably sure that it will not spill over
during the trip?
GIVEN:
Fish thank 12 in. x 24 in. x 12 in. partially filled with water to be transported in an
automobile. Tank partially filled with water (to a depth d in) subjected to constant linear
acceleration, ax. Tank height is 12 in.; length parallel to direction of motion is b in. Width
perpendicular to direction of motion is c in.
y

g
ax
d
x
0
b
FIND:
a). shape of free surface under constant ax.
b). Allowable water height, d, to avoid spilling as a function of ax and tank orientation.
c). optimum tank orientation and allowable depth.
SOLUTION:


 p   g   a
Basic equation:


 p
p  p 




  i  j  k     ig x  jg y  k g z     ia x  jay  k az 
y
z 




 x
Since p is not a function of z,
 i
i
p
 0 . Also, gx = 0, gy = –g, gz = 0 and ay = az =0
z
p
p
j
 jg  ia x
x
y
i
p
p
j
 jg  ia x
x
y
i
p
p
j
 jg  ia x
x
y
p
p
j
  jg  ia x
x
y
The component equations are:
p
  a x
x
p
  g
y
Since the pressure, p = p(x,y), the difference in pressure between two points (x,y) and (x+dx,
y+dy) is
dp 
p
p
dx  dy
x
y
Since the free surface is a line of constant pressure, then along the free surface, dp = 0 and
0
Therefore
p
p
dx  dy   a x dx  g dy
x
y
0   a x dx  g dy
g dy   a x dx
a
y 
 x

x  free surface
g
The free surface is a straight
g dy  a x dx
line 
In the diagram below,
d = original depth
e = height above the original depth
b = tank length parallel to direction of motion
e
b
b  dy 
b ax
tan    

2
2  dx  free surface 2 g
b

only valid for d  
2

y
e
e

12"

b/2
ax
d
tan  
0
x
b
e
e
b/2
b
tan 
2
We should align the tank with the long side perpendicular to the direction of motion, that is,
choose b = 12 in.
e
a
b ax
 6 x in.
2 g
g
The maximum allowable value of e = 12 – d in. Thus
12  d  6
ax
g
d max  12  6
and
If the maximum ax is assumed to be
2
3
ax
g
g , then allowable d = 8 in.
To allow a margin of safely, perhaps we should select d = 6 in.
Example 3.9
A cylindrical container, partially filled with a liquid, is rotated at a constant angular velocity,
ω, about its axis as shown in the diagram. After a short period of time there is no relative
motion, that is, the liquid rotates with the cylinder as if the system were a rigid body.
Determine the shape of the free surface.
z
R

g
h1
ho
r
ω
GIVEN:
A cylinder of liquid in solid-body rotation with angular velocity, ω, about its axis.
FIND:
The shape of the free surface.
SOLUTION:
Since p = p(r, z), the deferential change, dp, in pressure between two points with coordinates
(r, θ, z) and ( r + dr, θ, z + dz) is given by
dp 
p 
p 
 dr   dz
r  z
z  r
From Eq. 3.20 we have, for the z direction
p 
  g z  a z
z  r
Since gz = – g and az = 0, then
p 
  g
z  r
To obtain an expression for
p 
 , we apply Newton’s second law in the r direction
z  r
to a suitable differential element.
The pressure at the center of the element is p.
p dr dz
dr
d
2
p
p dr 
dr 

p
 r  d dz
r r 
2

r
p dr 
dr 

p
 r  d dz
r r 
2

d
2
p dr dz
The forces acting in the rθ plane on the element are shown in the diagram. Writing
Newton’s second law in the r direction, we have
 dF
r
 ar dm  ar  d   2 r d   2 r  r d dr dz
From the figure
 dF
r
p dr 
dr 
p dr 
dr 
d


p
 r   d dz   p 
 r   d dz  2 p dr dz sin
r 2 
2
r 2 
2
2


Expanding and canceling like terms, recognizing sin dθ/2 = dθ/2 (small angles)
2
2


dr
p dr p  dr 
dr
p dr p  dr 


 dFr  d dz  pr  p 2  r r 2  r  2   pr  p 2  r r 2  r  2   pdr 


 dF
r
 p 
 d dz  r dr 
 r 
Then
r
p
dr d dz   2 r r d dr dz
r
Dividing both sides by –r dr dθ dz results in
p
  2 r
r
p 
p 
 dr   dz
r  z
z  r
Since
dp 
Then
dp   2 r dr   g dz
To obtain the pressure difference between a reference point (r1, z1), where the pressure is p1,
and the arbitrary point (r, z), point (r, z), where the pressure is p, we must integrate.

p
p1
r
z
r1
z1
dp    2 rdr   gdz
p  p1 
 2
2
r
2

 r12  g z  z1 
Taking the reference point on the cylinder axis at the free surface gives
r1  0
p1  p atm
p  p atm 
Then
 2 r 2
2
z1  h1
 g z  h1 
Since the free surface is a surface of constant pressure ( p  p atm ), the equation of the free
surface is given by
0
 2 r 2
z  h1
or
2
 g z  h1 

r 2

2g
  R 2 ho
With rotation

R
0

z
0
R

 2r 2 
 r dr
2  r dz dr   2  z r dr   2  h1 
0
2 g 

R
 r 2  2r 4 
 2  2R4 
  2 h1 


h1R  4 g 
8 g  0
 2


Then

 2R4 
R 2 ho   h1 R 2 

4g 

and
Finally,
h1  ho 
z  h1
2g
R 2  r 2
4g
2g
2

R 2  1  r  


  

2 g  2  R  
z  ho 
z  ho
4g

r 2

z  ho 
z  ho
R 2
 R 2   r 2
4g
2g
2

 R 2  1  r  


  

2 g  2  R  
Any questions?