Download Congruence in Right Triangles 1

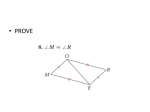
Congruence in Right Triangles
Name ________________________________
Right Triangle
Right Triangle – A triangle with one right angle. (90° angle).
Legs – The sides that form the right angle.
Hypotenuse – The side opposite the right angle. The longest side of the triangle.
Hypotenuse
Leg
Leg
Two sides and a non-included angle of one triangle are congruent to two sides and the nonincluded angle of another triangle.
Notice the two triangles are not congruent. Side-Side-Angle is not a valid method for proving
two triangles congruent.
However, this method works in the special case of right triangles where the right angles are the
non-included angles.
Hypotenuse-Leg (HL) Theorem
If the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of
another right triangle, then the triangles are congruent.
*** You must state that the triangles are RIGHT TRIANGLES in order to use the Hypotenuse
Leg Theorem***
X
Proof of HL Theorem
R
Y
P
1. Given: PS  RQ , PR  PQ
Prove: PRS  PQS
Statements
Reasons
R
S
Q
B
2. Given: PB  AB, PD  AD, AB  AD
A
P
Prove: ABP  ADP
D
Z
Statements
Reasons
C
3. Given: CD  EA , AD is the perpendicular bisector of CE
Prove: E  C
Statements
Reasons
A
B
E
D