* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Exponential Function
Integrating ADC wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Power MOSFET wikipedia , lookup
Electrical ballast wikipedia , lookup
Voltage regulator wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Current source wikipedia , lookup
Power electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Current mirror wikipedia , lookup
Opto-isolator wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
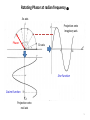
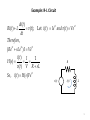
AC Circuit Analysis Represent sinusoidal signals by Ve jt where V cos(t ) Re Ve jt and j t V sin(t ) Im Ve 1 Exponential Function We focus on the exponential function est where s j d t Note: e et and et dt et dt d st But, e s est and est dt 1s est dt Properties of exponential function: (1) Essentially all waveforms encountered in practice can be expressed as a sum of exponential functions (2) The response of a “Linear Time-Invariant” (LTI) system to an exponential function e st is also an exponential function, H(s)e st So we only need to know H(s) – the transfer function. 2 The Complex Plane Remember, s j , where is radian frequency. LHP j RHP - What about negative frequencies? sin t e 2j cos t e 2 1 1 jt jt e jt e jt exponentially decreasing signals exponentially -j increasing signals 3 Imaginary axis projection with phase t t unit circle A phasor can represent either voltage or current. 4 Rotating Phasor at radian frequency Im axis Projection onto imaginary axis Phasor Re axis Sine Function Cosine Function Projection onto real axis 5 Voltage and current are in phase (0 ) Current leads voltage by 90 (= /2) Voltage leads current by 90 ? Resistor Capacitor Inductor Voltage in blue Current in red Phasors shown projected onto real axis. 6 Resistor : v(t ) i(t )R and i(t ) e st So v(t ) Re st v(t ) i( t ) 1 Z(s ) R ; Y (s) G i( t ) v(t ) R Inductor: v(t ) L di(t ) and i(t ) e st dt v(t ) sLe st v(t ) i( t ) 1 Z(s ) sL ; Y (s ) i( t ) v(t ) sL Capacitor: i(t ) C dv(t ) and v(t ) e st dt i(t ) sCe st i( t ) v(t ) 1 Y (s ) sC ; Z(s ) v(t ) i(t ) sC 7 A phasor is a complex number whose magnitude is the magnitude of a corresponding sinusoid, and whose phase is the phase of that corresponding sinusoid. A phasor is complex, and does not exist. Voltages and currents are real, and do exist. A voltage is not equal to its phasor. A current is not equal to its phasor. A phasor is a function of frequency, . A sinusoidal voltage or current is a function of time, t. The variable t does not appear in the phasor domain. The square root of –1, or j, does not appear in the time domain. Phasor variables are often given as upper-case boldface variables, with lowercase subscripts. For hand-drawn letters, a bar are typically placed over the variable to indicate that it is a phasor. 8 Example: R-L Circuit di(t ) Ri(t ) L v(t ); Let i(t ) Ie st and v(t ) Ve st dt Therefore , ( Re st sLe st )I Ve st i( t ) I 1 H (s) v(t ) V R sL R So , i(t ) H (s )Ve st v(t) i(t) L 9 General Form of H(s) Transfer Function H (s ) s s s 1 1 1 bn z 1 z2 zn H (s) am s s s 1 1 1 p 1 p 2 pm We must factor polynomials in variable s 10 A representative pole-zero diagram 11 Plot of H(s) 3 poles 2 zeros j http://lpsa.swarthmore.edu/Representations/SysRepZPK.html 12