Download Increasing and Decreasing Function

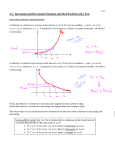
Increasing and Decreasing Functions
A function f is increasing on an interval if for any two numbers x1 and x 2 in the interval, x  x2 implies f x1   f x2 
Likewise, for decreasing
How to prove a function is increasing or decreasing using Calculus [ not our eyes or a calculator, Remember we are S-c-ho-l-a-r-s]
Let f be a function that is continuous on the closed interval [a, b] and differentiable on the open interval (a, b)
(1) If f x   0 for all x in (a, b), then f is increasing on [a, b]
(2) If f x   0 for all x in (a, b), then f is decreasing on [a, b]
(3) If f x   0 for all x in (a, b), then f is constant [ for example, f x   5 ]
A function is strictly monotonic if the function is either increasing on an entire interval, or decreasing on an entire
interval.
Let’s look at some functions [ without our TI]
1) Let f ( x)  4 x  x 2 on [-4, 4]
Step 1: Find f x  and the critical values for this interval
Step 2: Test Intervals
The First Derivative Test
Let c be a critical number [value] of a function f that is continuous on an open interval I containing c. If f is differentiable
on the interval, except possibly at c, then is: Then f c can be classified as follows:
If f x  changes from negative to possible values at x= c, then f has a relative minimum at c, f (c)
2) Consider y  x 2  4 on the interval  5,5
Our Analysis: The function is both continuous and differentiable on the interval.
Now let’s find the critical number (s):
Our critical number is___________
Interval
Sign of f (x )
Conclusion
5  x  0
0 x5
Since f x  is changing from negative to positive values at x=0, then f (x ) has a relative minimum value at of x=0. The
relative minimum value is ____ and it occurs at the point _______.
Here is a graph y  x 2  4 and y   2 x
If f x  changes from positive to negative values at x=c, then f has a relative maximum at c, f (c)
3) Consider f ( x)  5  2 x  x 2 on the interval (-4, 4)
Our Analysis: The function is both continuous and differentiable on the interval. Now let’s find any critical numbers.
Our critical number is_________
Our Analysis
Interval
Sign of f (x )
Conclusion
 4  x  1
1  x  4
Since f x  is changing from positive to negative values at x=-1, then f (x ) has a relative maximum value at x= ____.
The relative maximum value is ____ and it occurs at the point _______.
Here are the graphs of both f (x ) and f x 
If f x  is positive on both sides of x = c, then f c is neither a relative minimum or a relative maximum.
4) Consider f x   x 3  3 on (-3, 3), The function is both continuous and differentiable on the interval.
5)
Our critical value is at ___________
Our Analysis
Interval
Sign of f (x )
Conclusion
3  x  0
0 x3
In this case, we find there is neither a relative minimum nor a relative maximum at our critical value.
Here are the graphs of both f (x ) and f x 
Let’s try to analyze some more functions.
6) Let f ( x)  x 2  8x  10 ,  , 
This is our Mission:
(a) Find all critical numbers
(b) Find all open intervals where the function is increasing or decreasing
(c) Apply the First Derivative test to identify all relative extrema.
Our Analysis
Interval
Sign of f (x )
Conclusion
Statement about any extrema:
 ,4
 4, 
7) Let f ( x)  x  2 x  1
2
Critical Values:
Our Analysis
Interval
Sign of f (x )
Conclusion
Statement about extrema:
8) Use the graph of f (x ) below to answer the questions about f (x ) . Note that the graph is of f (x ) , the
derivative of f (x ) and not of f (x ) .
Based on the graph of f (x ) shown above find where the graph f (x ) is
increasing or decreasing AND find the x-values of any relative extrema.
9) Let y  f x  be the graph shown to the right
Based on the graph of f x  shown above find where the graph of f (x ) is increasing or decreasing and find the x-values
of any relative extrema.
10) The figure above shows the graph of f x  , the derivative of
the function f (x ) , for  7  x  7 . The graph of f x  has horizontal tangent lines at x =-3, x =2, and x =5 and a
vertical tangent at x=3. Find all relative extrema on the open interval -7 < x < 7. Justify completely.
11)A dog is observed running up and down a garden path. The function below models the dog’s velocity.
v(t )  t (t  2)(t  5) 2
At t=0, the dog is directly in front of the door. [Let’s consider the door to be “the origin”]
Describe the motion of the dog on the path
Is the speed of the dog increasing or decreasing at t=4?