Download Constant Functions "Flat Lines" and Linear Functions

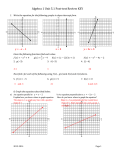
Constant Functions "Flat Lines" and Linear Functions "Lines
Lines can be flat, go up from left to right or go down from left to right. The slope is a
measurement that tells us just how much a line is going up or down.
m  slope
m  0 flat line
m  undefined, vertical line
m  0 line goes upward left to right
m  0 line goes downward left to right
m  1 diagonal going upward
m  −1 diagonal going downward
If we are given two points
P  x 1 , y 1  and Q  x 2 , y 2 
Then we can find the slope of the line between them by the formula
Rise
y −y
y −y
m  x 22 − x 11  x 11 − x 22 
Run
If x 1 and x 2 are the same the bottom part will be zero making the slope undefined.
Constant Functions
fx  NUMBER
Examples
fx  −3
gx  0
ht  6
y  −7
su  4
The graphs for these functions are flat lines with zero slope.
Their domain is the collection of all real numbers, −,  and their range is the single
item NUMBER .
1
fx  4 is a flat line crossing on the y axis at 4
y 5.0
4.5
4.0
3.5
-5
-4
-3
-2
-1
0
1
2
3
4
5
x
Linear Functions
Linear functions are of the format
fx  mx  b
The graphs for these functions are lines with a slope of "m" and a y intercept of "b".
The domain and range for all linear functions is −, 
fx  2x − 6
y
4
2
-5
-4
-3
-2
-1
-2
1
2
3
4
5
x
-4
-6
-8
-10
-12
-14
-16
2
Is a line going up with a slope of 2 and crossing on the y axis at -6
fx  −4x
y
20
10
-5
-4
-3
-2
-1
1
2
3
4
5
x
-10
-20
Is a line going down with a slope of -4 and is crossing through the origin since b  0.
Intercepts
X - intercepts
These are places where a function may or may not cross the x axis and can be found
by solving
fx  0
A generic function may have 0, 1, 2, 3, 4, ... any number of x intercepts.
For example on the linear function above
fx  2x − 6
the x intercept can be found
fx  2x − 6  0
2x − 6  0
x3
Y-intercepts
These are places where the function crosses the y axis and can be found by setting
x  0 or
3
f0  y intercept
fx  2x − 6
f0  20 − 6  −6
Popular Forms of Lines
Slope - Intercept
m  slope, b  y intercept
y  mx  b
Point Slope
m  slope, x 1 , y 1  any point on the line.
y − y 1   mx − x 1
General Form
ax  by  c
For the most part useless
Parallel and Perpendicular Lines
Parallel lines look like railroad tracks and they can be easily spotted in the slope
intercept form because the slope are THE SAME.
All of the following are parallel
y  3x  5
y  3x − 1
y  3x
y  3x  11
Perpendicular Lines intersect in a 90 degree angle and their slopes must satisfy the
following
m 1 ∗ m 2  −1
or said a different way
4
m 2  − m11
which means that one slope is the negative reciprocal of the other one.
The following ARE NOT perpendicular
y  3x  4
y  −3x − 1
since
3 ∗ −3  −9 and not − 1
The following ARE perpendicular
y  3x  4
y  −1x−1
3
Additional Comments
We want a line parallel to
2x − y  4
but notice in this format you cannot determine the slope. You MUST put it in slope
intercept form first.
y  2x − 4
So the slope of the new line will be 2.
We want a line perpendicular to
3x  4y  12
but again in this format you cannot determine the slope. You must put it in slope
intercept form first to see
m  −3
4
and then get the slope you need by taking the negative flip.
m perpendicular  4
3
5