Download Using Natural Image Priors

Using Natural Image Priors Maximizing or Sampling?
Thesis submitted for the degree of ”Master of Science”
Effi Levi
034337337
This work was carried out under the supervision of
Prof. Yair Weiss
School of Computer Science and Engineering
The Hebrew University of Jerusalem
Acknowledgments
First and foremost I would like to thank my advisor Prof. Yair Weiss for his guidance,
support and many hours spent on this work. I feel privileged for having had access to
his brilliant mind and ideas – never had I left his office with a question unanswered or
a problem unsolved. Thank you for your patience and willingness to not give up on me.
I would also like to thank my close friends, especially those who went through the
M.Sc with me – thanks to you I never felt alone.
And finally I would like to thank my family for constantly being there, through the
best and the worst, and for knowing not only when to help and support but also when
to give me space.
Contents
1 Introduction
5
1.1
Natural image statistics . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2
Image restoration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2.1
The common approach - MMSE/MAP . . . . . . . . . . . . . . .
7
1.2.2
Related Work . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.2.3
A different approach - sampling . . . . . . . . . . . . . . . . . . .
10
Sampling from image distributions . . . . . . . . . . . . . . . . . . . . .
11
1.3.1
Related work . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
Outline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.3
1.4
2 Fitting a GMM to the prior distribution
13
2.1
The Expectation-Maximization Algorithm . . . . . . . . . . . . . . . . .
13
2.2
Gaussian mixture model . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.3
Calculating the GMM fit . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.3.1
The E-step . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.3.2
The M-step . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
3 Algorithms for image inference
18
3.1
Non Gaussian distributions as marginal distributions . . . . . . . . . . .
18
3.2
Calculating the Maximum A Posteriori (MAP) estimate . . . . . . . . . .
19
3.3
Sampling from the prior . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
4
CONTENTS
3.4
Sampling from the posterior distribution . . . . . . . . . . . . . . . . . .
4 Experiments
23
26
4.1
The prior distribution
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
4.2
Experiments with synthetic images . . . . . . . . . . . . . . . . . . . . .
28
4.3
Experiments with natural images . . . . . . . . . . . . . . . . . . . . . .
29
5 Discussion
32
5.1
Results analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
5.2
Future work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
5.3
Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Chapter 1
Introduction
1.1
Natural image statistics
Consider the set of all possible images of size N × N . An image is represented by a
N × N matrix, therefore this set is actually a N × N linear space. Natural images - that
is, images consisting of ’real world’ scenes - take up a tiny fraction of the that space.
It would therefore make sense that both artificial and biological vision systems would
learn to characterize the distribution over natural images.
Unfortunately, this task is made very difficult by the nature of natural images. Aside
from being continuous and high dimensional signals, natural images also exhibit a very
non Gaussian distribution. It has been shown that when derivative-like filters are applied
to natural images the distribution of the filter output is highly non Gaussian - it is peaked
at zero and has heavy tails [11, 15, 13]. This property is remarkably robust and holds
for a wide range of natural scenes. Figure 1.1 shows a typical histogram of a derivative
filter applied to a natural image.
Many authors have used these properties of natural images to learn “natural image
prior probabilities” [17, 4, 6, 12, 14]. The most powerful priors are based on defining an
6
Chapter 1: Introduction
4
2.5
x 10
5
10
4
2
10
1.5
10
1
10
0.5
10
3
2
1
0
0
−0.5
−0.4
−0.3
−0.2
−0.1
a
0
0.1
0.2
0.3
0.4
0.5
b
10
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
c
Figure 1.1: a. A natural image, b. the histogram of a derivative filter applied to the
image and c. the log histogram.
energy E(x) for an image x of the form:
E(x) =
X
Eiα (fiα (x))
(1.1)
i,α
Where fiα (x) is the output of the ith filter in location α and Ei (·) is a non quadratic
energy function. By defining P (x) =
1 −E(x)
e
Z
P (x) =
this gives:
1Y
Ψi (fiα (x))
Z i,α
(1.2)
Where Ψ(·) is a non-Gaussian potential. Typically the filters are assumed to be zero
mean filters (e.g. derivatives). Figure 1.2 shows a typical energy function (left) and
potential function (right).
Once these priors are learnt, they can be used to create sample images; they can also
be combined with an observation model to perform image restoration. In this work, we
focus on the problem of how to use the prior.
1.2
Image restoration
The problem of image restoration typically consists of restoring an ”original image” x
from an observed image y. Two common examples of this problem are image inpaint-
7
2
1
1.8
0.9
1.6
0.8
1.4
0.7
1.2
0.6
1
Ψ
energy
Chapter 1: Introduction
0.5
0.8
0.4
0.6
0.3
0.4
0.2
0.2
0.1
0
−10
−5
0
filter output
5
10
0
−10
Energy
−5
0
filter output
5
10
Potential
Figure 1.2: Left: The energy function defined over derivative outputs that was learned
by Zhu and Mumford [17]. Right: The potential function e−E(x) . The blue curves
show the original function and the red curves are approximations as a mixture of 50
Gaussians. In this work we use this mixture approximation to derive efficient sampling
procedures.
ing, which involves inpainting various holes applied to the original image and image
denoising, which involves removing random noise added to the original image (typically
Gaussian). Both assume the additive noise model:
y =x+w
(1.3)
Where w is the noise added to the image x. This model naturally describes the image
denoising problem; However, it can also be adapted to describe the image inpainting
problem by setting the noise to be infinity in the hole areas and zero elsewhere.
1.2.1
The common approach - MMSE/MAP
In general Bayesian estimation, the common approach is minimizing/maximizing some
function defined on the observation and the known prior distribution. The MMSE
(Minimum Mean Square Error) method involves minimizing the MSE (mean of the
squared error) E[x − x∗]. Under some weak regularity assumptions [7] the estimator is
8
Chapter 1: Introduction
given by:
x∗ = E[x|y]
(1.4)
The MAP (Maximum A Posteriori) method, on the other hand, involves maximizing
the posterior probability:
x∗ = argmax P (x|y)
(1.5)
x
However, as illustrated in figure 1.3, this approach can be problematic for image
processing. In this figure, we used Gaussian “fractal” priors to generate images. We
then artificially put a “hole” in the image by setting some of the pixels to zero, and
used Bayesian estimators to fill in the hole. For a Gaussian prior, the MMSE and MAP
estimators are identical and they both suffer from the same problem — as the size of
the hole grows, the Bayesian estimators are increasingly flat images.
This makes sense since the Gaussian density is maximized at a flat image. But these
flat images are certainly not plausible reconstructions. A similar effect can be seen when
we artificially add noise to the images, and ask the Bayesian estimators to denoise them.
Again, as the amount of noise increases, the Bayesian estimators are increasingly flat.
1.2.2
Related Work
Despite the shortcomings of the MAP/MMSE approach described above, the vast majority of research in image restoration utilizes either MAP or MMSE (e.g. [13, 14, 1, 5,
16, 9]).
The work of Bertalmio et al [1] is one example of using the MAP approach. They
used a form of diffusion to fill in the pixels in hole areas in the image. Another good
example for using the MAP approach is the work of Levin, Zomet and Weiss [8]; they
used histograms of local features to build an exponential family distribution over images,
then used it to inpaint holes in an image by finding the most probable image, given the
boundary and the prior distribution.
A very successful example of the MAP approach to image denoising and inpainting
is the work of Roth and Black [14]. They extended the Product of Experts framework
Chapter 1: Introduction
9
image
hole
MAP/MMSE
posterior sample
image
hole
MAP/MMSE
posterior sample
image
noised
MAP/MMSE
posterior sample
Figure 1.3: Inpainting (top & middle) and denoising (bottom) an image sampled from
a Gaussian fractal prior. The Bayesian estimators (MAP/MMSE) are equivalent in this
case and both converge to overly smooth images as the measurement uncertainty increases. The posterior samples, on the other hand, do not suffer from the same problem.
In this work we show how to sample efficiently from the posterior when non Gaussian
image priors are used.
10
Chapter 1: Introduction
(introduced by Welling et al [4]) to model distributions over full images. in their Field
of Experts model, each expert uses a local linear operator followed by a student T
distribution. The probability distribution of an image is a product of nonlinear functions
applied to linear filters learned specifically for this task (similar to the exponential family
form in equation 1.2) where the local filters and the nonlinear functions are learned using
contrastive divergence. Given a noisy image, the MAP image can be inferred using
gradient ascent on the posterior.
In the image processing community, the MMSE approach is most popular for the
image denoising problem. A good example for this approach is the work of Portilla
et al [13]; they showed that the very non Gaussian marginal statistics of filter outputs
can be obtained by marginalizing out a zero mean Gaussian variable whose variance σ 2
is itself a random variable. Conditioned on the value of σ 2 the filter output distribution is Gaussian, but the unconditional distribution is a (possibly infinite) mixture of
Gaussians. They used this observation to model the distribution of local filter outputs
by explicitly modeling the local distribution over the variances, then used a Bayesian
inference algorithm to denoise natural images.
1.2.3
A different approach - sampling
This problem with MAP and MMSE estimators for image processing has been pointed
out by Fieguth [3]. He argued that by sampling from the posterior probability, one can
obtain much more plausible reconstructions, and presented efficient sampling strategies
for Gaussian priors. The rightmost samples in figure 1.3 shows the posterior samples.
Indeed, they do not suffer from the same problem as MAP and MMSE. Although many
efficient sampling strategies for Gaussians exist, obtaining high quality results in image
processing require non-Gaussian priors.
Chapter 1: Introduction
1.3
11
Sampling from image distributions
The common approach towards sampling from a non-Gaussian distribution is using
Gibbs sampling. Given a joint distribution over N random variables:
P (x) = P (x1 , x2 , ..., xN )
(1.6)
It is assumed that while integrating over the joint distribution may be very difficult,
sampling from the conditional distributions P (xj |{xi }i6=j ) is relatively a simple task.
Every single iteration consists of sampling one variable at a time (denoted single-site
Gibbs sampling):
xt+1
∼ P (x1 |xt2 , xt3 , xt4 , ..., xtN )
1
(1.7)
t
t
t
xt+1
∼ P (x2 |xt+1
2
1 , x2 , x4 , ..., xN )
(1.8)
t+1
t
t
xt+1
∼ P (x3 |xt+1
3
1 , x2 , x4 , ..., xN )
..
.
(1.9)
t+1
t+1
t+1
xt+1
∼ P (xN |xt+1
1 , x2 , x3 , ..., xN −1 )
N
(1.10)
Since Gibbs sampling is a Metropolis method [10], the distribution P (xt ) converges
to P (x) as t → ∞.
1.3.1
Related work
In [17], Zhu and Mumford used Gibbs sampling to sample images from the prior distribution over natural images they had learnt. They encountered two well-known disadvantages of the Gibb sampler:
• Single-site Gibbs sampling takes very long to reach equilibrium for distributions
over natural images.
• The complexity of Gibbs sampling grows with the number of possible discrete
values of the filter outputs.
12
Chapter 1: Introduction
In later work [19, 18] Zhu et al attempted using blocked Gibbs sampling for faster
convergence. This involves sampling groups (or blocks) of variables instead of just one
at a time. While somewhat reducing the time needed for convergence, they still needed
to use heavy quantization to limit the complexity of the algorithm.
1.4
Outline
In this work we will present an efficient method to sample from the posterior distribution
when using non Gaussian natural image priors.
• First, we will introduce an efficient EM algorithm to calculate the MAP from the
prior distribution and the observed image.
• Then, by slightly altering the algorithm, we will derive an efficient algorithm for
sampling from a known prior distribution.
• Finally, we will show how - using this algorithm - we are able to sample from any
posterior distribution given the prior distribution and an observed image.
Chapter 2
Fitting a GMM to the prior
distribution
All the algorithms presented in this work utilize a prior distribution over images in the
form of a Gaussian mixture model (GMM). We used the prior distribution learnt in [17];
however, we needed a way to convert this prior to GMM form. In this chapter we will
demonstrate how to fit a GMM to a prior distribution. This EM-based method for fitting
a GMM is a well known and widely used method, and we describe it here in order to
provide a complete description of our work.
2.1
The Expectation-Maximization Algorithm
The EM algorithm was first formally introduced (and named) by Dempster, Laird and
Rubin [2]. We are presented with an observed data set X which is generated by some
distribution with a parameter vector Θ. Assuming that a complete data (X , H) exists,
the EM algorithm is used to compute the Maximum Likelihood Estimate (MLE).
This is done iteratively, where each iteration consists of two steps:
The E-step: calculate the expected value of the log-likelihood of the complete-data
log P (X , H; Θ) with respect to the unobserved data H given the observed data X and
14
Chapter 2: Fitting a GMM to the prior distribution
the current parameter estimates Θt . The E-step in iteration t is:
Q(Θ|Θt ) = E[log P (X , H; Θ)|X , Θt ]
X
=
log P (X , H; Θ) · P (h|X , Θ)
(2.1)
(2.2)
h∈H
The M-step: maximize the expectation calculated in the E-step with respect to the
parameter vector Θ:
Θt+1 = argmax Q(Θ|Θt )
(2.3)
Θ
2.2
Gaussian mixture model
A Gaussian mixture model (GMM) is a convex combination of Gaussians, each
with a (potentially) different mean and variance. More formally:
P (x) =
X
πj G(x; µj , σj2 )
(2.4)
− 12 (x−µj )2
1
e 2σj
πj q
2πσj2
(2.5)
j
=
X
j
Where ∀j : πj > 0 and
P
j
πj = 1. In theory the sum may be infinite; however, for
obvious reasons, we will limit our discussion to a finite GMM.
2.3
Calculating the GMM fit
We assume the probabilistic model given in equation 2.5. Given the observed data set
x = x1 , x2 , ..., xN 1 , we wish to estimate the parameters Θ = {πj , µj , σj2 }M
j=1 . We can
1
Note that x is an observed data set. In our work we needed to fit a GMM to an analytic probability
function (the potential functions learnt in [17]). This was achieved by generating a very large data set
from the analytic probability function and then fitting the GMM to that data set.
Chapter 2: Fitting a GMM to the prior distribution
15
think of this as if each xn is generated from one of the M hidden states, each with its
own (Gaussian) probability. Let’s denote hn to be the state of xn , where hn ∈ {1...M }.
We get:
log P (X |Θ) = log
N
Y
P (xn |Θ) =
n=1
N
X
log
n=1
M
X
πj G(xn ; µj , σj2 )
Given the values of H:
N
N
X
X
log P (X , H|Θ) =
log(P (xn |hn )P (hn )) =
log(πhn G(xn ; µhn , σh2n ))
n=1
2.3.1
(2.6)
j=1
(2.7)
n=1
The E-step
In the E-step we calculate:
Q(Θ|Θt )
=
X
log P (X , H|Θ)P (h|X , Θt )
(2.8)
h∈H
=
M X
N
X
log(πj G(xn ; µj , σj2 ))P (j|xn , Θt )
(2.9)
j=1 n=1
=
M X
N
X
log(πj )P (j|xn , Θt )
j=1 n=1
+
M X
N
X
log G(xn ; µj , σj2 )P (j|xn , Θt )
(2.10)
j=1 n=1
Let’s denote:
ωjn = P (j|xn , Θt )
P (xn |j, Θt )P (j|Θt )
=
P (xn |Θt )
P (xn |j, Θt )P (j|Θt )
= PM
t
t
k=1 P (xn |k, Θ )P (k|Θ )
(2.11)
(2.12)
(2.13)
2
πjt G(xn ; µtj , σjt )
= PM
k=1
(2.14)
πkt G(xn ; µtk , σkt 2 )
In conclusion, the E-step is given by:
Q(Θ|Θt ) =
M X
N
X
j=1 n=1
log(πj )ωjn +
M X
N
X
j=1 n=1
2
log G(xn ; µtj , σjt )ωjn
(2.15)
16
Chapter 2: Fitting a GMM to the prior distribution
2.3.2
The M-step
The M-step is performed separately for each of the parameters πj , µj and σj2 .
M-step for πj :
argmax
{πj }
M X
N
X
log(πj )ωjn
such that
j=1 n=1
M
X
πj = 1
(2.16)
j=1
In order to do that we introduce a Lagrange multiplier λ with the above constraint
and solve:
"M N
!#
M
X
∂ XX
n
log(πj )ωj + λ
πj − 1
=0
∂πj j=1 n=1
j=1
(2.17)
The solution is given by:
N
1 X n
ω
πj =
N n=1 j
(2.18)
M-step for µj :
argmin
{µj }
N
X
1
(xn − µj )2 ωjn
2
σ
n=1 j
(2.19)
Is given by the solution of:
#
" N
∂ X 1
(−2xn µj + µ2j )ωjn = 0
∂µj n=1 σj2
N
X
(−2xn + 2µj )ωjn = 0
(2.20)
(2.21)
n=1
µj
N
X
ωjn
=
n=1
N
X
xn ωjn
(2.22)
n=1
Or:
PN
n=1
µj = P
N
xn ωjn
n
n=1 ωj
(2.23)
Chapter 2: Fitting a GMM to the prior distribution
17
M-step for σj2 :
N
X
1
argmin
{σj2 }
n=1
2
[log σj2 +
1
(xn − µj )2 ]ωjn
σj2
(2.24)
Taking the derivative with respect to σj2 and equating to zero, we get:
N
X
1
1
[ 2 − 2 2 (xn − µj )2 ]ωjn = 0
σ
(σj )
n=1 j
σj2
N
X
ωjn
N
X
=
(xn − µj )2 ωjn
n=1
(2.25)
(2.26)
n=1
And finally:
PN
σj2
=
2 n
n=1 (xn − µj ) ωj
PN
n
n=1 ωj
(2.27)
Chapter 3
Algorithms for image inference
3.1
Non Gaussian distributions as marginal distributions
The algorithms we have developed are based on the assumption that every factor Ψi (·)
can be well fit with a mixture of Gaussians:
Ψi (·) =
X
πij G(·; µij , σij2 )
(3.1)
j
We now define a second probability distribution over two variables - the image x and
a discrete label field hiα . For every filter i and location α, hiα says which Gaussian is
responsible for that filter output. The joint distribution is given by:
P (h, x) =
1Y
2
πi,hiα G(fiα (x); µi,hiα , σi,h
)
iα
Z i,α
(3.2)
We will now show that the marginal probability over x in P (h, x) is equal to P (x):
Chapter 3: Algorithms for image inference
X
P (h, x) =
h
=
=
=
=
X1Y
2
πi,hiα G(fiα (x); µi,hiα , σi,h
)
iα
Z
i,α
h
1 XY
2
πi,hiα G(fiα (x); µi,hiα , σi,h
)
iα
Z h i,α
1 YX
2
πi,hiα G(fiα (x); µi,hiα , σi,h
)
iα
Z i,α h
iα
1 YX
πij G(fiα (x); µij , σij2 )
Z i,α j
1Y
Ψi (fiα (x))
Z i,α
= P (x)
19
(3.3)
(3.4)
(3.5)
(3.6)
(3.7)
(3.8)
The complete data log probability can be written as:
log P (x, h) = − log Z +
1
πij
− 2 (fiα (x) − µij )2 )
δ(hiα − j)(ln √
2σij
2πσij
i,α,j
X
(3.9)
Using this rewrite it is clear that conditioned on x the hidden label field is independent (the energy contains no cross terms) and that conditioned on h the image is a
Gaussian Random field (the energy is quadratic in x).
3.2
Calculating the Maximum A Posteriori (MAP)
estimate
We now show how to calculate the MAP estimate, given a prior distribution, using an
EM algorithm. The generative model is:
y =x+w
(3.10)
Where w ∼ N (0, ΣN ) and a prior on x given by a mixture of Gaussians on the output
of a set of filters:
20
Chapter 3: Algorithms for image inference
P (fiα (x)) =
X
πij G(fiα (x); µij , σij2 )
(3.11)
j
This generative model can be used to model the inpainting problem — where certain
pixels have infinite noise and others have no noise, as well as the denoising problem —
where typically all pixels will have the same noise.
We are given an observed image y and want to calculate the MAP x. This is done
by maximizing the log of the posterior probability:
X
1
log P (f, y; x) = − (x − y)T Σ−1
ln Ψi (fiα (x))
N (x − y) +
2
i,α
(3.12)
As seen in section 3.1 the complete log probability - the log probability of x,y as well
as the hidden variable h - is:
X
1
πij
1
− 2 (fiα (x) − µij )2 )
log P (f, y, h; x) = − (x − y)T Σ−1
δ(hiα − j)(ln √
N (x − y) +
2
2πσij 2σij
i,α,j
(3.13)
Before describing an algorithm for finding the MAP, we point out an obvious shortcoming of the approach:
Observation: Assume the potentials functions Ψ(·) are peaked at zero and the
filters are zero mean. When the noise increases (ΣN → ∞), the posterior is maximized
by a constant function.
Despite this shortcoming, the MAP approach can work very well when the observation process forces us to choose non-flat images. Indeed, many successful applications
of MAP artificially increase the weight of the likelihood term to avoid getting overly
smooth solutions [14].
To find the MAP estimate we can use an EM algorithm (see section 2.1). The
observed data is the observed image y, the unobserved data is the field labels h we
defined earlier, and we would like to estimate x (the ”original image”). In the E step
we calculate the expected value of equation 3.12, and in the M step we maximize it.
Chapter 3: Algorithms for image inference
21
E step: compute the expected value with respect to h. Since everything is linear in
h except the δ function we obtain:
X
1
πij
1
E[log P (f, y, h; x)] = − (x − y)T Σ−1
(x
−
y)
+
wiαj (ln √
− 2 (fiα (x) − µij )2 )
N
2
2πσij 2σij
i,α,j
(3.14)
With:
wiαj = P (hiα = j|y; x)
−
πij
e
σij
= P
1
2σ 2
ij
(3.15)
(fiα (x)−µij )2
1
2 (fiα (x)−µik )
πik − 2σik
k σik e
(3.16)
2
M step: maximize equation 3.14 with respect to x. This is equivalent to maximizing:
1
1X
Q(x) = − (x − y)T Σ−1
(F x − µ~j )T Wj (F x − µ~j )
(x
−
y)
−
N
2
2 j
Where Wj is a diagonal matrix whose iαth element is Wj (iα, iα) =
wiαj
2 ,
σij
(3.17)
µ~j is a
vector whose iαth element is µij and F is a matrix containing the set of filters. Note
that the equation is quadratic in x so it can be maximized using only linear methods.
∂Q
1
1X
= − (x − y)T Σ−1
(F x − µ~j )T Wj F
N −
∂x
2
2 j
1
1 T −
1 TX T
1X T
F Wj F +
µ~j Wj F
= − xT Σ−1
N + y ΣN 1 − x
2
2
2
2
j
j
(3.18)
(3.19)
And when we equate the gradient to zero we get:
!
Σ−1
N +
X
F T Wj F
x = Σ−1
N y+
j
3.3
X
F T Wj µ~j
(3.20)
j
Sampling from the prior
The EM algorithm described above can be readily adapted to produce samples from the
prior (see [4, 12] for a similar algorithm for the special case of T distribution factors).
22
Chapter 3: Algorithms for image inference
Rather than estimating the expectation of the hidden variables as in EM, we simply
sample their values. The result is blocked Gibbs sampling by iterating sampling P (h|x)
and P (x|h).
Sampling h:
P (hiα = j|x) ∝
πij − 2σ1ij (fiα (x)−µij )2
e
σij2
(3.21)
Sampling x:
T Σ−1 (F x−µ)
P (x|h) ∝ e−(F x−µ)
(3.22)
Where the elements of µ and Σ are computed according to the values of hiα sampled
in the previous step. Taking the derivative of log P (x|h) and equating to zero gives us:
E(x|h) = (F T Σ−1 F )−1 F T Σ−1 µ
(3.23)
And the 2nd derivative gives us:
V ar(x|h) = (F T Σ−1 F )−1
(3.24)
We can sample from this distribution without inverting large matrices. All that is
needed is the ability to solve sparse sets of linear equations. Let’s define a new variable
z ∼ N (µ, Σ), and solve the problem:
x∗ = argmin(F x − z)T Σ−1 (F x − z)
(3.25)
x
The solution is given by:
x∗ = (F T Σ−1 F )−1 F T Σ−1 z
(3.26)
which yields E(x∗ ) = E(x|h) and V ar(x∗ ) = V ar(x|h).
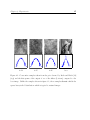
Figure 3.1 shows samples 14 to 16 taken from the sparse prior learned by Zhu and
Mumford [17] compared to a natural image (the lena image). In this prior, the filters
used are horizontal and vertical derivatives as well as the Laplacian filter. Zhu and
Chapter 3: Algorithms for image inference
23
Mumford used a training set of 44 natural images to learn the potential functions using
maximum likelihood. The learnt potentials are peaked at zero and have the property
that samples from prior have the same filter-output histograms as the natural images
in the training set (this was verified by Zhu and Mumford by using single site Gibbs
sampling to sample from their prior).
We can make two observations:
1. Even though we cannot prove mixing of our samples, after a relatively small number of iterations the samples have the correct filter-output histograms. This suggests (but of course does not prove) rapid mixing.
2. While the samples change from one iteration to the next, their histograms remain
constant.
An important thing to note is that this EM-based sampling algorithm is much faster
to converge than the Gibbs sampling method (discussed in section 1.3). Convergence to
the shown histogram was achieved in under 5 EM iterations, while the EM iterations
themselves are relatively easy to compute. It is also important to note that this algorithm
does not require using heavy quantization, as opposed to the Gibbs sampling method.
3.4
Sampling from the posterior distribution
Our final goal is to sample from the posterior distribution:
P (x|y) ∝ P (x|h)P (y|x)
Since P (y|x) ∝ e−(x−y)
T Σ−1 (x−y)
N
(3.27)
we get:
T Σ−1 (F x−µ)−(x−y)T Σ−1 (x−y)
N
P (x|y) ∝ e−(F x−µ)
(3.28)
24
Chapter 3: Algorithms for image inference
t=14
t=15
t=16
lena
Figure 3.1: Consecutive samples taken from the sparse prior learned by Zhu and Mumford [17] (top) and the histograms of the Laplacian filter outputs (bottom), compared
to the lena image.
 


 
F
Σ 0
µ
, µ̂ =   we get:
If we define F̂ =  , Σ̂ = 
I
0 ΣN
y
T Σ̂−1 (F̂ x−µ̂)
P (x|y) ∝ e−(F̂ x−µ̂)
(3.29)
And the sampling can be done using the same procedure we described above.
In this case:
z ∼ N (µ̂, Σ̂)
(3.30)
 
zx
Since Σ̂ is diagonal, z is actually consisted of two independent parts: z =   where
zy
zx ∼ N (µ, Σ) and zy ∼ N (y, ΣN ).
Chapter 3: Algorithms for image inference
x∗ = (F̂ T Σ̂−1 F̂ )−1 F̂ T Σ̂−1 z



 
i Σ−1 0
h
i Σ−1 0
F −1 h
z
  )
= ( F T IT 
F T IT 
−1
−1
0 ΣN
0 ΣN
I
 
h
i F
h
i
−1
−1
−1
T
−1
T
−1


=( F Σ
)
ΣN
F Σ
ΣN z
I
h
i
−1
−1 z
T −1
= (F T Σ−1 F + Σ−1
)
F
Σ
Σ
N
N
−1
−1
T −1
= (F T Σ−1 F + Σ−1
N ) (F Σ zx + ΣN zy )
25
(3.31)
(3.32)
(3.33)
(3.34)
(3.35)
Observation: when ΣN → ∞ then typical samples from the posterior will be typical
samples from the prior.
Although this observation is trivial, it highlights the advantage of posterior sampling over MAP estimation. Whereas MAP estimation will produce flat images as the
measurement uncertainty increases, posterior sampling will produce typical images from
the prior. If the prior is learnt using maximum likelihood, this means that posterior
sampling will produce images with the same filter-output histogram as natural images,
whereas MAP estimation will produce images with the wrong filter-output histogram.
Chapter 4
Experiments
4.1
The prior distribution
The first step in our experiments was to choose a set of filters and the prior distribution
associated with this set. Initially we intended to use the filters and prior learned by
Roth and Black in [14]. However, when we sampled from that prior, using the algorithm
described in section 3.3, we discovered that the distribution of the filters’ outputs on
the samples are very different from the sparse heavy-tailed distribution which is typical
to natural images. Instead, they resemble a more Gaussian-looking distribution (see
figure 4.1).
We therefore decided to use the prior functions learned by Zhu and Mumford [17]
discussed in section 3.3. We fitted a Gaussian mixture model to those prior functions
(using the method described in chapter 2), then applied our algorithm (described in
section 3.3) to produce a series of 64 × 64 samples from that prior. As can be seen in
figure 3.1, these samples exhibit the expected form of distribution, which is identical to
that of a natural image (the lena image).
Chapter 4: Experiments
t=14
27
t=15
t=16
lena
Figure 4.1: Consecutive samples taken from the prior learned by Roth and Black [14]
(top) and the histograms of the output of one of the filters (bottom), compared to the
lena image. Unlike the samples shown in figure 3.1, these samples do not exhibit the
sparse heavy-tailed distribution which is typical to natural images.
28
Chapter 4: Experiments
image
hole
MAP
posterior sample
image
hole
MAP
posterior sample
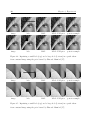
Figure 4.2: Inpainting an image sampled from a sparse prior learned by Zhu and Mumford [17] with a small hole (top) and a large hole (bottom).
4.2
Experiments with synthetic images
We proceeded to use the Zhu and Mumford prior together with the MAP estimation
algorithm and the posterior sampling algorithm described in sections 3.2 and 3.4 to
inpaint various holes in the sampled images. The results are shown in figure 4.2. Note
that when the hole is small, the MAP estimation is equal to the posterior sample, but
when the hole is very large the MAP estimation converges to a smooth image (in the
hole area) while the posterior sample exhibits no such behavior.
Next we tested the MAP estimation algorithm and the posterior sampling algorithm
on noised versions of our samples. The results are shown in figure 4.3. The same
observation can be made as in the inpainting experiment: as the noise’s level increases,
the MAP estimation becomes very smooth, unlike the posterior sample.
Chapter 4: Experiments
29
image
noised
MAP
posterior sample
image
noised
MAP
posterior sample
Figure 4.3: Denoising an image sampled from a sparse prior learned by Zhu and Mumford [17] with a low level of noise (top) and a high level of noise (bottom).
4.3
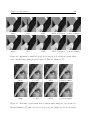
Experiments with natural images
For the next experiment we selected a 64 × 64 patch from a natural image (the lena
image) and again used MAP estimation algorithm and the posterior sampling algorithm
to inpaint various holes in the selected patch. To verify that these failures of MAP are
not specific to the Zhu et al prior, we also ran the MAP denoising code with the filters
and prior learned by Roth and Black in [14] on the same holes. The same convergence
to a smooth image can be observed. The results are shown in figures 4.4, 4.5 and 4.6.
In the final experiment we used the MAP estimation algorithm and the posterior
sampling algorithm to denoise two levels of noises applied to the selected patch. The
results are shown in figure 4.7.
It is important to note that the weight of the likelihood term (in the MAP cost function) was not artificially increased, unlike the common practice in denoising algorithms
(e.g. [14]). This way the results represent the true MAP estimation.
30
Chapter 4: Experiments
image
hole
MAP
MAP - FoE prior
posterior sample
image
hole
MAP
MAP - FoE prior
posterior sample
Figure 4.4: Inpainting a small hole (top) and a large hole (bottom) in a patch taken
from a natural image using the prior learned by Zhu and Mumford [17].
image
hole
MAP
MAP - FoE prior
posterior sample
image
hole
MAP
MAP - FoE prior
posterior sample
Figure 4.5: Inpainting a small hole (top) and a large hole (bottom) in a patch taken
from a natural image using the prior learned by Zhu and Mumford [17].
Chapter 4: Experiments
31
image
hole
MAP
MAP - FoE prior
posterior sample
image
hole
MAP
MAP - FoE prior
posterior sample
Figure 4.6: Inpainting a small hole (top) and a large hole (bottom) in a patch taken
from a natural image using the prior learned by Zhu and Mumford [17].
image
σ = 2.5%
MAP
posterior sample
image
σ = 10%
MAP
posterior sample
Figure 4.7: Denoising a patch taken from a natural image using the prior learned by
Zhu and Mumford [17] with a low level of noise (top) and a high level of noise (bottom).
Chapter 5
Discussion
5.1
Results analysis
By using our algorithm to sample from a known prior, not only have we produced a
set of synthetic images which exhibit this prior, but we have also insured that the set
of filters used to sample is sufficient to capture all the features in those images. When
we used our MAP and posterior sampling algorithms to inpaint small holes and denoise
a low level of noise in the sampled images, we obtained very good results with both
algorithms. However, when inpainting large holes and denoising high levels of noise, we
showed that the sampling from the posterior distribution is definitely preferable over
calculating the MAP estimate.
The results on natural images, however, were less satisfactory. The posterior sample
does avoid the overly smooth reconstructions given by the MAP estimate, however the
samples do not look completely natural. This is to be expected from the simple form
of the prior (that was learned using three very simple filters) which is hardly enough to
capture all the features of natural images. Surely better prior models will improve the
performance. At the same time, it is important to realize that ”better” prior models for
MAP estimation may not be better for posterior sampling. In particular, we have found
that the Roth and Black prior (learned using contrastive divergence) may work better
Chapter 5: Discussion
33
than the Zhu and Mumford prior for MAP estimation, but sampling from the Roth and
Black prior does not reproduce the statistics of natural images.
5.2
Future work
As mentioned above, we believe that using better prior models when sampling from the
posterior will immensely improve the results. The posterior sampling algorithm seems to
be much more dependent on the accuracy of the prior used than the MAP algorithm. As
stated by Zhu and Mumford in [17], using multi-scale filters should improve the results
(by capturing more global features in the images). Multi-orientation filters are probably
also a good idea, assisting in capturing different angles and orientations in the images.
5.3
Summary
Non-Gaussian overcomplete priors are used in many image processing applications but
pose computational difficulties. By embedding the images in a joint distribution over
images and a hidden label field, one can utilize a prior distribution over natural images
in the form of a Gaussian mixture model. In this work we explored the things that can
be accomplished using this prior distribution.
We presented an algorithm for efficiently sampling from a given prior, as well as
an EM algorithm for calculating the MAP estimate over an observed image. We then
introduced an efficient algorithm to sample from the posterior distribution of an observed image (given a prior distribution). We demonstrated the advantages of using the
posterior sampling approach over the MAP estimation approach, and discussed possible
improvements to the model presented here. We hope that the efficient sampling method
we presented here will enable learning better priors.
Finally, we have shown here an efficient method to sample from a posterior distribution given a prior distribution and an observed data set. While our work was derived
34
Chapter 5: Discussion
by the need to utilize natural image statistics, and the experiments were performed on
digital images, the method presented here is a general method that could potentially
be used on any type of data, making it (possibly) useful in other areas of digital signal
processing.
Bibliography
[1] Marcelo Bertalmio, Guillermo Sapiro, Vincent Caselles, and Coloma Ballester. Image inpainting. In SIGGRAPH ’00: Proceedings of the 27th annual conference on
Computer graphics and interactive techniques, pages 417–424, New York, NY, USA,
2000. ACM Press/Addison-Wesley Publishing Co.
[2] A. P. Dempster, N. M. Laird, and D. B. Rubin. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society. Series B
(Methodological), 39(1):1–38, 1977.
[3] Paul W. Fieguth. Hierarchical posterior sampling for images and random fields. In
ICIP (1), pages 821–824, 2003.
[4] G. E. Hinton and Y. W Teh. Discovering multiple constraints that are frequently approximately satisfied. In Proceedings of Uncertainty in Artificial Intelligence (UAI2001), 2001.
[5] Jianhong (jackie) Shen. Inpainting and the fundamental problem of image processing. SIAM News, 36:2003, 2003.
[6] Y. Karklin and M.S. Lewicki. Learning higher-order structures in natural images.
Network: Computation in Neural Systems, pages 14: 483–499, 2003.
[7] E. L. Lehmann and George Casella. Theory of Point Estimation (Springer Texts in
Statistics). Springer, September 2003.
36
BIBLIOGRAPHY
[8] Anat Levin, Assaf Zomet, and Yair Weiss. Learning how to inpaint from global
image statistics. Computer Vision, IEEE International Conference on, 1:305, 2003.
[9] E. H. Adelson M. F. Tappen, C. Liu and W. T. Freeman. Learning gaussian conditional random fields for low-level vision. In The Proceedings of the IEEE Computer
Society Conference on Computer Vision and Pattern Recognition (CVPR), 2007.
[10] David J. C. MacKay. Information Theory, Inference, and Learning Algorithms.
Cambridge University Press, 2003.
[11] B.A. Olshausen and D. J. Field. Emergence of simple-cell receptive field properties
by learning a sparse code for natural images. Nature, 381:607–608, 1996.
[12] S. Osindero, M. Welling, and G. E. Hinton. Topographic product models applied
to natural scene statistics. Neural Computation, 18:2006, 2005.
[13] J Portilla, V Strela, M Wainwright, and E P Simoncelli. Image denoising using
scale mixtures of gaussians in the wavelet domain. IEEE Trans Image Processing,
12(11):1338–1351, 2003.
[14] S. Roth and M. J. Black. Fields of experts: A framework for learning image priors.
In IEEE Conf. on Computer Vision and Pattern Recognition, 2005.
[15] E.P. Simoncelli. Statistical models for images:compression restoration and synthesis.
In Proc Asilomar Conference on Signals, Systems and Computers, pages 673–678,
1997.
[16] M. F. Tappen. Utilizing variational optimization to learn markov random fields.
In The Proceedings of the IEEE Computer Society Conference on Computer Vision
and Pattern Recognition (CVPR), 2007.
[17] S. C. Zhu and D. Mumford. Prior learning and gibbs reaction-diffusion. IEEE
Trans. on Pattern Analysis and Machine Intelligence, 19(11):1236–1250, 1997.
BIBLIOGRAPHY
37
[18] S.C. Zhu and X.W. Liu. Learning in gibbsian fields: How fast and how accurate
can it be? IEEE Trans on PAMI, 2002.
[19] Song Chun Zhu, Xiu Wen Liu, and Ying Nian Wu. Exploring texture ensembles by
efficient markov chain monte carlo-toward a ’trichromacy’ theory of texture. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 22(6):554–569, 2000.