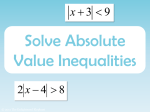Download 1-5 Solving Inequalities

1-5 Solving
Inequalities
Solve and graph inequalities by using
properties of inequalities.
Graphing Inequalities
• Open dot for < or >
• Closed dot for ≥ or ≤
• If the inequality symbol is open toward the variable,
shade to the right.
• If the inequality symbol is pointed toward the
variable, shade to the left.
Writing an Inequality
from a Sentence
• What inequality represents “five fewer than a
number is at least 12”?
• What numbers are we dealing with?
• Any variables?
• What words indicate an operation?
• What words indicate an inequality?
• X – 5 ≥ 12
Properties of Inequalities
• If you multiply or divide both sides of an inequality
by a negative number, the symbol flips.
Solving
•
•
•
•
•
•
•
Use inverse operations
−3 2𝑥 − 5 + 1 ≥ 4
−6𝑥 + 15 + 1 ≥ 4
−6𝑥 + 16 ≥ 4
−6𝑥 ≥ −12
𝑥≤2
Graph the solution
No Solution or All Real
Numbers
• There is no solution if all variables cancel and the
statement is false.
o Ex: -2 > 7 (no variables and we know that -2 is not greater than 7)
• All real numbers are solutions if all variables cancel
and the statement is true.
o Ex: -15 ≤ 8 (no variables and it is true that -15 is less than 8)
o Same as infinitely many solutions
Compound Inequality
• Consists of two distinct inequalities
joined by the word and or the word or
• You can find the solutions by
identifying where the solutions overlap
or by combining the solutions to form a
larger solution set.
Using the word “And”
• Contains the overlap of the graphs
of two inequalities that form a
compound inequality.
• EX: x ≥ 3 and x ≤ 7
• Can also be written 3 ≤ x ≤ 7
o This is only for a compound
inequality using the word “and”
Using the word “Or”
• Contains each graph of the two
inequalities that form the compound
inequality.
• Used when there is no overlap.
• EX: x < -2 or x ≥ 1
Writing a Compound
Inequality
• All numbers that are greater than -2
and less than 6
• Key information
• n > -2 and n < 6
• -2 < n and n < 6
• -2 < n < 6
• Graph
Solving
• A solution to a compound inequality
involving and is any number that
makes both inequalities true.
• EX: -3 ≤ m – 4 < -1
• Isolate the variable by adding 4 to
each piece
• -3 + 4 ≤ m – 4 + 4 < -1 + 4
• 1≤m<3
Solving
• A solution to a compound inequality
involving or is any number that makes
either inequality true.
• You must solve each inequality
separately.
• EX: 3t + 2 < -7 or -4t + 5 < 1
• 3t < -9 or -4t < -4
• t < -3 or t > 1
1-6 Absolute
Value Equations
and Inequalities
Write and solve absolute value equations
and inequalities by applying the definition
of absolute value.
Solving an Absolute Value
Equation
• What are the solutions of |x| + 2 = 9
• Solve using inverse operations
• |x| = 7 so… what is x?
• x = 7 or x = -7
• Why?
Key Concept
• What about |2x – 5| = 13?
• To solve an equation in the form |A| = b, where A
represents a variable expression, solve both A = b
and A = -b.
• When solving, always isolate the absolute value
expression first. Do not use inverse operations on
what is inside.
• 2x – 5 =13 and 2x – 5 = -13
• x = 9 or x = -4
Practice
• Solve the following:
• 2|x + 5| - 2 = 6
• |3x – 7| + 3 = 20
Absolute Value Equations
• Since the absolute value is the distance between a
number and zero, an absolute value cannot be
negative.
• Solve 3|2z + 9| + 12 = 10
• Subtract 12: 3|2z + 9| = -2
2
• Divide by 3: |2z + 9| = 3
• Absolute value cannot be negative so there is no
solution
• Be sure to check for extraneous solutions, meaning a
solution which does not satisfy the original equation.
• Ex: when you solve 3𝑥 + 2 = 4𝑥 + 5, you get the
solutions x = -3 or x = -1.
o if you substitute these into the original equation, you will find that x = -3 does
not satisfy the equation and x = -1 does. So, x = -3 is extraneous and is not a
solution.
Inequalities
• The same method can be applied to solving
absolute value inequalities.
• 2 2𝑥 + 4 − 3 ≥ 9
• Start by using inverse operations to isolate the
absolute value expression.
• 2|2𝑥 + 4| ≥ 12
add 3
• |2𝑥 + 4| ≥ 6
divide by 2
• 2𝑥 + 4 ≥ 6 𝑜𝑟 2𝑥 + 4 ≤ −6
o Notice that the symbol is reversed when you take the opposite sign.
• 2𝑥 ≥ 2 𝑜𝑟 2𝑥 ≤ −10
• 𝑥 ≥ 1 𝑜𝑟 𝑥 ≤ −5
• Graph
subtract 4
Assignment
• Odds p.38 #27-31, 39, 43
•
p.46 #43-47, 57-61